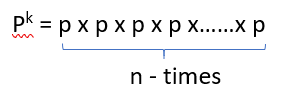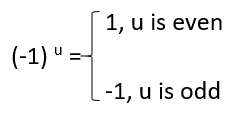• In mathematical expression, which includes division and multiplication of decimal values of large number, it becomes quite complicated to solve these expressions.
• So, to reduce this complexity we use approximation method. In approximation method, we need not calculate the exact value of an expression, but we calculate the nearest (round off) values.
• When we use approximation method, then final result obtained is not equal to the exact result, but it is very close to the final result (either a little less or little more).

Basic Rules to Solve the Problems by Approximation:

Rule1:

To solve the complex mathematical expression, take the nearest value of numbers given in the expression.

Rule 2:

To multiply large number, we can take the approximate value (round off) of numbers by increasing one number and decreasing the other accordingly, so that the calculation is eased.

Rule 3:

When we divide large number with decimals, then we can increase or decrease both numbers accordingly.

Rule 4:

To find the percentage of any number, we can use the following shortcut methods

To calculate 10% of any number, we simply put a decimal after a digit from the right end.

To calculate 1% of any number, we simply put a decimal after two digits from right end.

To calculate 25% of any number, we simply divide the number by 4.

Examples:

1. 89% of (599.88 + 30 x 400) + 50 =?

Solution:

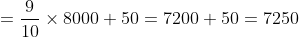
 2.  

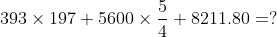
Solution: 393 x 197 + 5600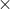 

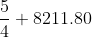
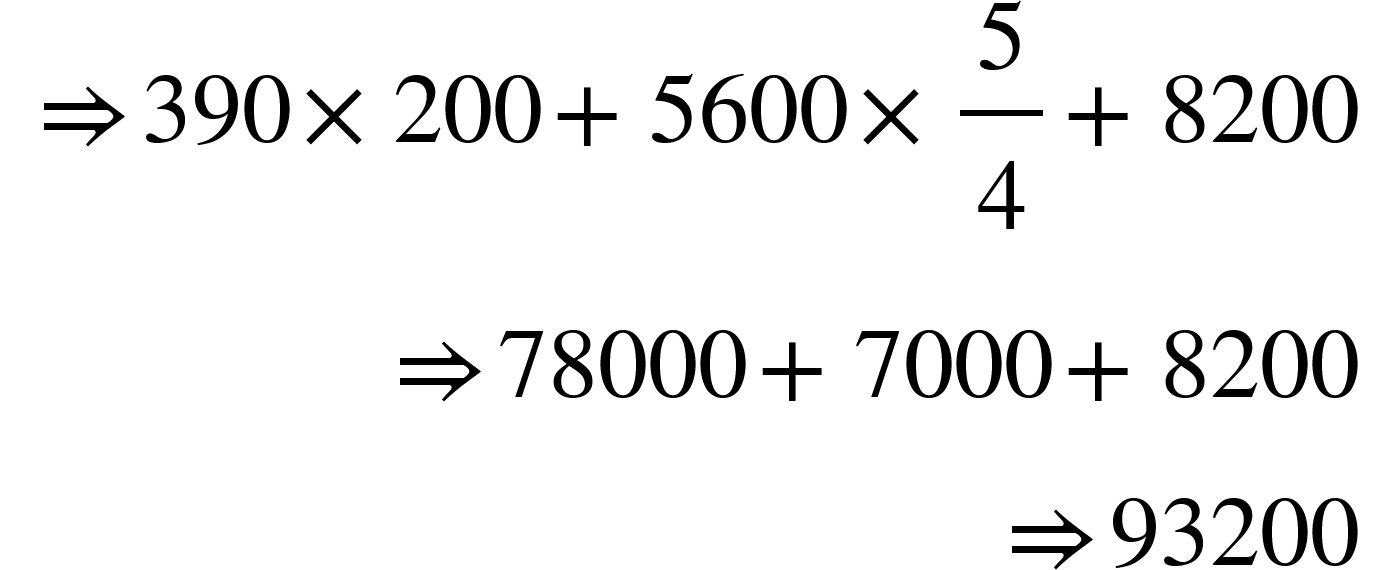
 3. (9.5)² =?

Solution: (9.5)² = 90.25 = 90

 4. 18^3.5 ÷ 27^3.5 x 6^3.5 = 2^?

Solution:  18^3.5 ÷ 27^3.5 x 6^3.5 = 2^?

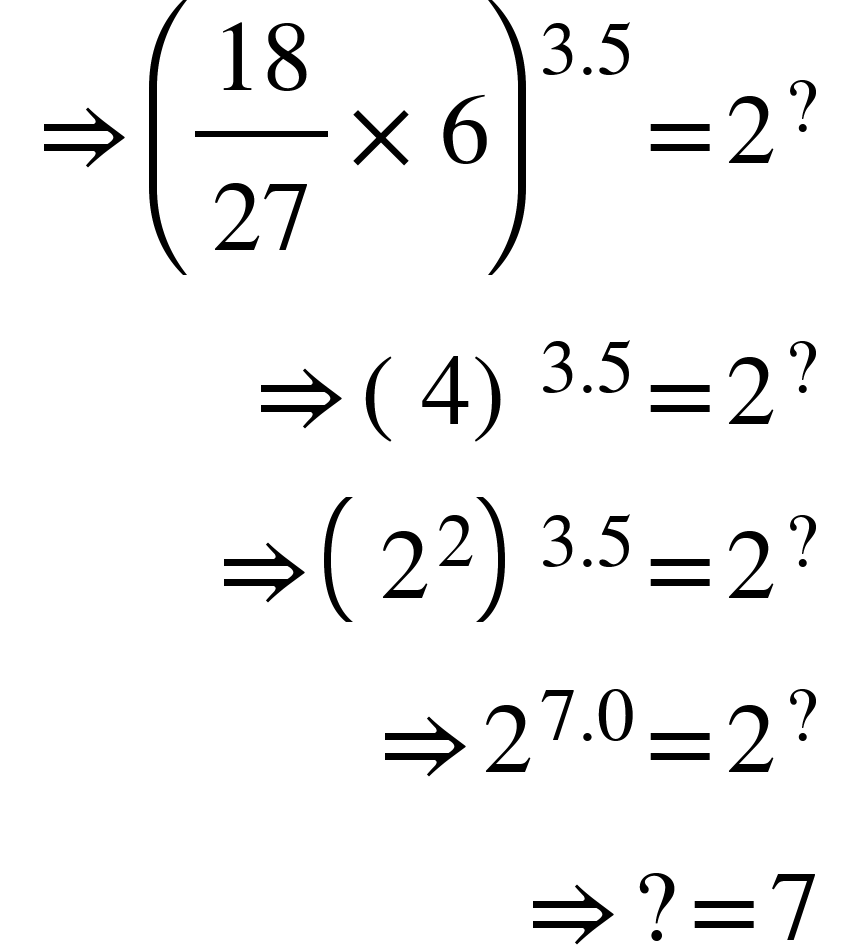
 5. 125.009 + 69.999 + 104.989 =?

Solution:

125.009 + 69.999 + 104.989 =?

 Each value is approximated to nearest whole number

=> ? =125 + 70 + 105

=> ? = 300

---

1. Direct Proportion:

Two quantities are said to be directly proportional, if on the increase (or decrease) of the one, the other increase (or decreases) to the same extent.

Example1: Cost is directly proportional to the number of articles (More Articles, More Cost)

Example2: Work done is directly proportional to the number of men working on it. (More Men, More work)

2. Indirect Proportion:

Two quantities are said to be indirectly proportional, if on the increase of the one, the other decreases to the same extent and vice-versa.

Example1: The time taken by a car in covering a certain distance is inversely proportional to the speed of the car.

(More speed, less is the time taken to cover a distance)

Example2: Time taken to finish a work is inversely proportional to the number of persons working at it.

(More persons, less is the time taken to finish a job)

Note: In solving questions by chain rule, we compare every item with the term to be found out.

Examples:

1. If the price of 6 toys is $ 264.37, what will be the approximate price of 5 toys?

Solution: Let the required price be $ x.

Then, less toys, less cost (Direct Proportion)

Therefore, 6: 5:: 264.37: x

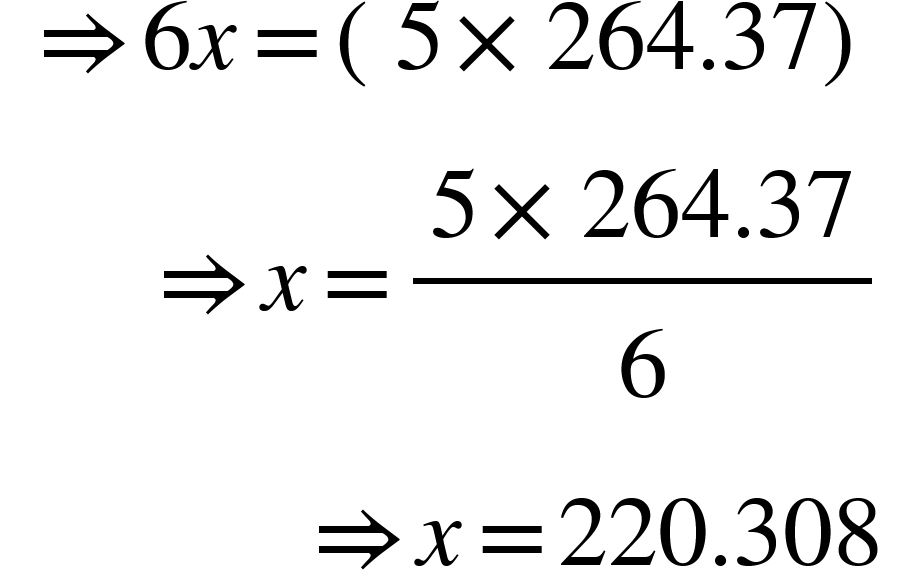
 2. 36 men can complete a piece of work in 18 days. In how many days will 27 men complete the same work?

Solution: Let the required number of days be x.

Then, less men, more days (Indirect proportion)

Therefore, 27: 36:: 18: x

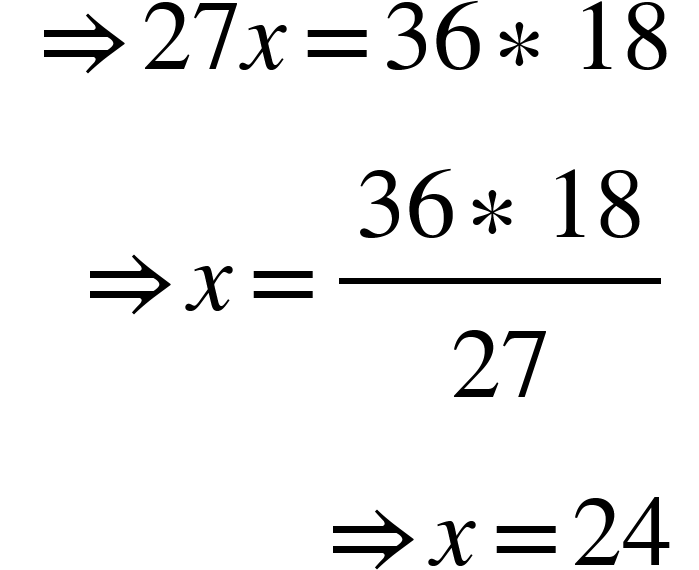
 3. In a dairy farm, 40 cows eat 40 bags of husk in 40 days. In how many days one cow will eat one bag of husk?

Solution:

• Let the required number of days b x.
• Less cows, More days (Indirect Proportion)
• Less bags, Less days (Direct Proportion)

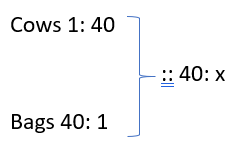
Therefore, 1 * 40 * x = 40 * 1 * 40

 x = 40

1. If the cost of x meters of wire is d dollars, then what is the cost of y metres of wire at the same rate?

Solution:

 5. If  of a cistern is filled in 1 minute, how much more time will be required to fill the rest of it?

Solution:

• Let the required time be ‘x’ seconds.
• Part filled = 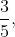 Remaining part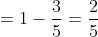 
• Less part, Less time (Direct proportion)

---

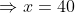
To start a big business or an industry, a large amount of money is needed.  It is beyond the capacity of or two persons to arrange such a huge amount. However, some persons associate together to form a company. They, then, draft a proposal, issue a prospectus (in the name of the company), explaining the plan of the project and invite the public to invest money in this project. They, thus, pool up the funds from the public, by assigning them shares of company.

Important Formulae:

1. Stock-capital: The total amount of money needed to run the company is called the stock-capital.
2. Shares or Stock: The whole capital is divided in to small units, called shares or stock.

For each investment, the company issues a share-certificate, showing the value of each share and the number of shares held by a person.

The person who subscribes in shares or stock is called a shareholder or stock holder.

3. Dividend: The annual profit distributed among shareholders is called dividend.

Dividend is paid annually as per share or as a percentage.

4. Face Value: The value of a share or stock printed on the share-certificate is called its Face Value or Nominal Value or Par value.
5. Market Value: The stocks of different companies are sold and bought in the open market through brokers at stock-exchanges. A share (or stock) is said to be:

1. At premium, if its market value is more than its face value
2. At par, if its market value is the same as its face value
3. At discount or Below par, if its market value is less than its face value.

Thus, if a $100 stock is quoted at a premium of 18, then market value of the stock = $(100 + 18) = $ 118

Likewise, if a $ 100 stocked at a discount of 5, then the market value of the stock = $ (100 – 5) = $ 95

6. Brokerage: The broker’s charge is called brokerage

1. When stock is purchased, brokerage is added to the cost price.
2. When stock is sold, brokerage is subtracted from the selling price.

NOTE:

• The face value of a share always remains the same
• The market value of a share changes from time to time
• Dividend is always paid on the face value of a share.
• Number of shares held by a person

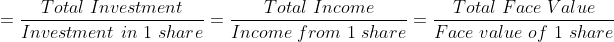
Examples:

1. Find the annual income derived from $ 2500, 8% stock at 106.

Solution: Income from $ 100 stock = $ 8

Income from $ 2500 stock = $ = $ 200

 2. A man buys $ 25 shares in a company which pays 9 % dividend. The money invested is such that it gives 10% on investment. At what price did he buy the shares?

Solution: Suppose he buys each share for $ x.

x = 22.50

Cost of each share = $ 22.50

 3. A man invests in a 16% stock at 128. The interest obtained by him is?

Solution: By investing $ 128, income derived = 16

Therefore, interest obtained = 12.5%

 4. To produce an annual income of $ 1200 from 12% stock at 90, the amount of stock needed is:

Solution: For an income of $ 12, stock needed = $ 100

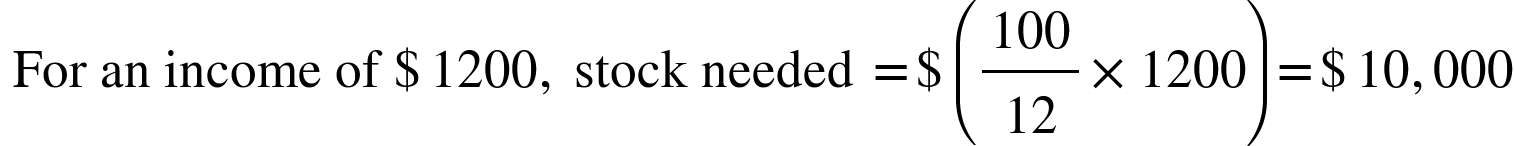
 5. A invested some money in 10% stock at 96. If B wants to invest in an equally good 12% stock, he must purchase a stock worth of:

Solution: For an income of $ 10, investment = $ 96

---

Speed

The rate at which a body or an object travels to cover a certain distance is called speed of that body.

Time

The duration in hours, minutes or seconds spent to cover a certain distance is called the time. Distance

The length of the path travelled by any object or a person between two places is known as distance.

Relation between Speed, Time and Distance:

Speed is the distance covered by an object in unit time. It is calculated by dividing the distance by the time taken.

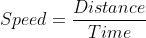
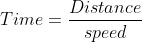
Distance = Speed x time

Formulae:

1. If speed is kept constant, then the distance covered by an object is proportional to time.

Distance 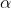 Time (speed constant) or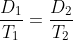 

 2. If time is kept constant, then the distance covered by an object is proportional to speed.

Distance 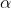 Speed (speed constant) or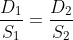 

 3. If distance is kept constant, then the speed covered by a body is inversely proportional to time.

Speed 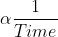 (distance constant) or S₁ T₁ = S₂ T₂ = S₃ T₃ = ….

 4. When two bodies A and B are moving with speed a miles/h and b miles/h respectively, then the relative speed of two bodies is

1.  (a + b) miles/h (if they are moving in opposite direction)
2. (a - b) miles/h (if they are moving in same direction)

 5. When a body travels with different speeds for different durations, then average speed of that body for the complete Journey is defined as the total distance covered by the body divided by the total time taken to cover the distance.

Average speed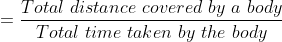

Note: If a body covers a distance D₁ at S₁ miles/h, D₂ at S₂ miles/h, D₃ at S₃ miles/h and so on up to D_n at S_n, then Average speed =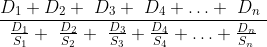

Examples:

1. A train covers a distance of 200 miles with a speed of 10 miles/h. What time is taken by the train to cover this distance?

Solution: Given, speed = 10 miles/h and distance = 200 miles

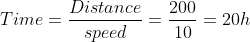
Therefore, required time = 20 h

 2. A person covers a distance of 12 miles, while walking at a speed of 4 miles/h. How much distance he would cover in same time, if he walks at a speed of 6 miles/h?

Solution: Given that, D₁ = 12 miles, S₁ = 4 miles/h, D₂ =? and S₂ = 6 miles/h

Since, the time is kept constant.

According to the formula,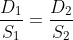 

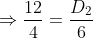
 D₂ = 18 miles

Therefore, the person will cover 18 miles.

 3. A person covers a certain distance with a speed of 18 miles/h in 8 min. If he wants to cover the same distance in 6 min, what should be his speed?

Solution: We know that, Speed =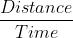 

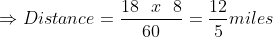
 4. Two trains are running in the same direction. The speeds of two trains are 5 miles/h and 15 miles/h, respectively. What will be the relative speed of second train with respect to first?

Solution: We know that, if two trains are running in same direction, then difference in speeds is the required relative speed.

Required relative speed = 15 - 5 = 10 miles/h

 5. A person covers a distance of 20 miles by bus in 35 min. After deboarding the bus, he took rest for 20 min and covers another 10 miles by a taxi in 20 min. Find his average speed for the whole journey?

Solution: Total distance covered = (20 + 10) miles = 30 miles

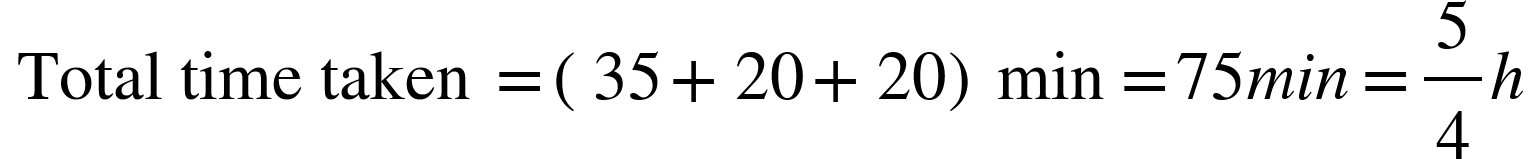
According to the formula, Average speed =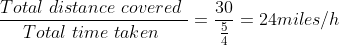 

So, the average speed of the person for the whole journey is 24 miles/h

---

A race or a game of skill includes the contestants in a contest and their skill in the concerned contest/game.

Important Terms

Race

A race is a contest of speed in running, driving, riding, sailing or rowing.

Race Course

The ground/path on which a contest is organised in a systematic way, is called a race course. Starting Point

The exact point/place from where a race begins, is called starting point.

Start

If two persons A and B are contesting a race and before the start of the race, A is at the starting point and B is ahead of A by 20 m, then it is said that A gives B a start of 20 m.

Finishing Point

The exact point/place where a race ends, is known as finishing point.

Winning Point/Goal

 A person who reaches the finishing point first, is called the winner.

Note

For a winner, finishing point is as same as the winning point/goal

Dead Heat Race

A race is said to be a dead heat race, if all the contestants reach the finishing point exactly at the same time.

Game

A game of 100 means that the contestant who scores 100 points first, is declared the winner.

Some Facts about Race

 For Two Contestants A and B

1. If A beats B by x m, then

Distance covered by A (winner) = L m Distance covered by B (loser) = (L - x) m

 2. If B starts from x m ahead of A (or A gives B a start of x m), then

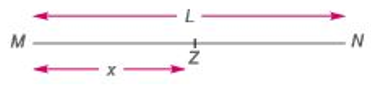
A start from M and B starts from Z. Distance covered by B = (L - x) m

 3. If A beats B by T s, then

A and B both start from point M.

Time taken by A (winner) = Time taken by B (loser) - T

It means that A completes the race in T s less time than that of B

 4. If B starts the race T s before the time A starts (or if A gives B a start of T s), then

In such case, we say that A starts T s after the time B starts. 5. If both of the contestants get at the finishing point at the same time, then Difference in time of defeat = 0; Difference in distance of defeat = 0

Examples:

1. In a game of 100 points, A scores 100 points, while B scores only 75 points. In this game, how many points can A give to B? S

Solution: Given

• Score of A = 100 points;
• Score of B = 75 points

.^.. A can give (100 - 75) = 25 points to B

2. In a 100 m race, Jack runs at the speed of 4 km/h. Jack gives Bob a start of 4 m and still beats him by 15 s. Find the speed of Bob?

Solution:

• Time taken by Jack to cover 100 m = 
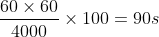
• Therefore, Bob covers (100 – 4) = 96 m in (90 + 5) = 105 s

So, Bob’s speed =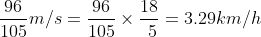 

 3. A 10 km race is organised at 800 m circular race course. P and Q are the contestants of this race. If the ratio of the speeds of P and Q is 5: 4, how many times will the winner overtake the loser?

Solution: Given Speed of P: Speed of Q = 5: 4

• Time taken by P to cover 5 rounds = Time taken by Q to cover 4 rounds
• Distance covered by P in 5 rounds 
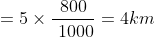
• Distance covered by Q in 4 rounds 
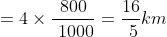
• In 5 rounds, P will overtake Q every time.
• It means that after covering 4 km, P will overtake Q one time.

Therefore, after covering 10 km P will overtake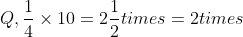 

 4. In a 200 m race, A can beat B by 50 m and B can beat C by 8 m. In the same race, A can beat C by what distance?

Solution:

• From given data we can write, A: B = 200: 150 and B: C = 200: 192
• 
• So, A beats C by (200 – 144) m = 56 m

 5. In a game of billiards, A can give 20 points in the game of 120 points and he can give C 30 points in the game of 120 points. How many points can B give C in a game of 90?

Solution:

• If A scores 120 points, then B scores 100 points and C scores 90 points.
• When B scores 100 points, then C scores 90 points.
• When B scores 90 points, then C scores points = 81 points.
• Therefore, B can give C, 9 points in a game of 90.

---

Problems based on trains are same as the problems related to 'Speed, Time and Distance' and some concepts of 'Speed, Time and Distance' are also applicable to these problems.

The only difference is that the length of the moving object (train) is taken into consideration in these types of problems

Rules:

Rule 1:  Speed of train (S) = 

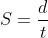
Here, unit of speed is m/s or km/h

1. a km/h
2. a m/s

Rule 2:  

The distance covered by train in passing a pole or a standing man or a signal post or any other object (of negligible length) is equal to the length of the train.

Rule 3:  

If a train passes a stationary object (bridge, platform etc;) having some length, then the distance covered by train is equal to the sum of the lengths of train and that particular stationary object which it is passing

Rule 3:  

If two trains are moving in opposite directions, then their relative speed is equal to the sum of the speeds of both the trains.

Rule 4:  

If two trains are moving in the same direction, then the relative speed is the difference of speeds of both trains.

Rule 5:  

If two trains of lengths x and y are moving in opposite directions with speeds of u and v respectively, then time taken by the trains to cross each other is equal to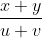 

Rule 6:  

If two trains of lengths x and y are moving in the same direction with speeds of u and v respectively, then time taken by the faster train to cross the slower train is equal to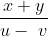 

Rule 7:  

If two trains start at the same time from points P and Q towards each other and after crossing each other, they take t₁, and t₂ time in reaching points Q and P respectively, then (P's speed): (Q's speed) = t₁: t₂

Examples:

1. A train takes 9 s to cross a pole. If the speed of the train is 48 km/h, then length of the train is

Solution:

• Let the length of the train be x m.
• Now, speed = 48 km/h 
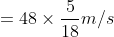
• Train takes 9 s to cross a pole.

• Therefore, length of train(x) = speed x time 

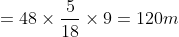
 2. The distance between two stations P and Q is 145 km. A train with speed of 25 km/h leaves station at 8:00 am towards station Q. Another train with speed of 35 km/h leaves station Q at 9:00 am towards station P. Then, at what time both trains meet?

Solution:

• First train leaves at 8:00 am and second at 9:00 am.
• So, first train i.e., from P to Q has covered 25 km distance in 1 h.
• So, distance left between the station =145-25 = 120 km
• Now, trains are travelling in opposite directions
• So, relative speed = 25 + 35 = 60 km/h
• Time taken to cover 120 km 

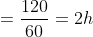
Therefore, the time at which both the trains will meet, is 2 h after second train left i.e., 9:00 am + 2h = 11:00 am

 3. A train A is 180 m long, while another train B is 240 m long. A has a speed of 30 km/h and B's speed is 40 km/h. If the trains move in opposite directions, find when will A pass B completely?

Solution: Let the total distance = x + y = 180 + 240 = 420 m

            Active speed 

Therefore, required time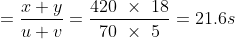 

 4. Train A crosses a pole in 25 s and train B crosses the pole in 1 min 15 s. Length of train A is half the length of train B. What is the ratio between the speeds of A and B, respectively?

Solution:

• Let the lengths of trains A and B be l and 2l respectively
• When a train crosses a pole, it covers the distance equal to its length

Therefore, required ratio of speeds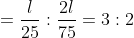 

 5. A train overtakes two persons walking along a railway track. The first one walks at 4.5 km/h and the other one walks at 5.4 km/h. The train needs 8.4 s and 8.5 s respectively, to overtake them. What is the speed of the train, if both the persons are walking in the same direction as the train?

Solution: Speed of 1^st person = 4.5 km/h 

Speed of 2^nd person = 5.4 km/h 

Let the speed of the train be k m/s

Then, (k – 1.25) x 8.4 = (k – 1.5) x 8.5

8.4k – 10.5 = 8.5k – 12.75

0.1k = 2.25

k = 22.5

Therefore, speed of train 

 

---

Escalator problems are similar to the upstream and downstream problems.

Here the escalator moves in both the directions but in a stream, the direction of flow of water is constant.

These escalator questions are bit confusing compared to other topics in time, speed and distance.

Escalator:

• An escalator is a moving stair, i.e., it moves continuously up or down.
• The total number of stairs are fixed in an escalator always.
• The distance is said in terms of the number of steps.
• The number of steps taken by the individual and the escalator is equal to the total number of steps on the escalator.

Important Things:

1. If we are moving with escalator, we have to climb less steps as escalator will push us forward on its own.
2. If we are moving against the escalator, we have to climb more steps as escalator will pull us back on its own.

Moving with escalator:

The total number of steps will be the addition of the two (individual and escalator) in case the individual is moving in the same direction as that of the escalator.

Total number of steps = steps climbed by individual + steps of escalator

Moving against escalator:

The total number of steps will be the subtraction of the two (individual and escalator) in case the escalator and the individual are moving in the opposite direction.

Total number of steps = steps climbed by individual - steps of escalator

Note:

The time taken by the individual to climb up or down the escalator is equal to the time for which escalator is moving.

Common Questions based on escalator:

1. Speed scenario
2. Steps scenario
3. Time scenario

Examples:

1. A boy is walking down a downward-moving escalator and steps down 15 steps to reach the bottom. Just as he reaches the bottom of the escalator, he remembers that he forgot his wallet in a shop on the floor above. He runs back up the downward moving escalator at a speed 3 times that which he walked down. He covers 45 steps in reaching the top. How many steps are visible on the escalator when it is switched off?

Solution:

Given that boy runs back at a speed 3 times that which he walked down

Let the boy’s speed with the escalator = s

And boy’s speed against the escalator = 3s

And speed of escalator = u

We know that total number of steps in both cases are equal.

15 + (15/s) times u = 45 – (45/3s) times u

(30/s) times u = 45 -15

(1/s) times u = 30/30 = 1

Placing the value in any of the equation = 15 + 15 = 30

Number of steps visible on the escalator when it is switched off = 30

2. A lady walks up on an escalator which is moving up at a rate of one step per second, thirty steps bring her top. The other day she goes up at three steps per second, reaching the top in 45 steps. Find the number of steps in the escalator?

Solution: The time taken on two days are 30s and 15s which are in ratio 2: 1.

So, the steps thrown out by the escalator are in ratio 2: 1

 30 + 2x = 45 + x

  x = 15

Therefore, total steps = 30 + 2(15) = 60

3. Richard takes 60 seconds to walk up on an upward moving escalator but he takes 90 seconds to walk up on a downward moving escalator. Calculate the time that Richard will take to walk up if the escalator is not moving?

Solution:

Let us consider the speed of Richard be u

Let us consider the speed of escalator be v

As the distance is constant, the three speeds i.e., u + v, u, u – v will be in arithmetic progression.

Since time is inversely proportional to speed, the time taken in each case will be in harmonic progression.

Calculating the harmonic mean of the given time taken = the time taken by Richard to walk up if the escalator is not moving = (2 * 60 * 90)/ (60 + 90) = 10800/150 = 72

4. Bob is going up the escalator. It takes Bob 60 seconds to walk up the escalator which is moving upwards and 180 seconds to walk up the escalator which is moving downwards. Calculate the time taken by Bob to climb the escalator which is stationary.

Solution:

• Let speed of Bob be "s" steps per second.
• Let speed of escalator be "e" steps per second.
• No. of steps (N)= 60s + 60e

Since Bob is moving upwards, 90e will be added

• No. of steps= 180s-180e

Since Bob is moving downwards, 150e will be subtracted

By equating the number of steps,

60s + 60e = 180s -180e

s = 2e

• N = 60s + 60e = 60s + 60(s/2) = 60s + 30s = 90s
• Time taken when escalator is stationary = 90s/s = 90 seconds

N=80a+80x= 80a+16a=96a Time taken when the escalator is stationary= 96a/a= 96seconds.

5. An escalator moves downward from first floor to ground floor at a constant rate. When the escalator is turned off, Harry takes 90 steps to descend from first floor to ground floor. When the escalator is turned on, Harry needs only 40 steps to descend from first to ground floor. If Harry begins at ground floor and walks upward, against the escalator’s downward movement, how many steps will he need to take to reach first floor Assuming that Harry walks at a constant rate in all scenarios.

Solution:

  Let the distance from first to ground floor = d

  Let speed be u with which Harry moves when escalator is still

  Let the speed be v with which escalator moves up or down

When escalator is stand still, he needs 90 steps

 Therefore d/u = 90 => u = d/90 ............. (I)

Also, when both escalator and Harry moves in same direction, he needs 40 steps

  Therefore d/ (u +v) = 40 => u + v = d/40 ........... (II)

  Solving both (i) & (ii)

we get v= d/ (72) ..........(iii)

   Hence u - v = d/ (35x72)

Therefore, Number of steps required when escalator and Harry are moving in opposite directions = d/(u-v) = d/ (d/(35x72)) = 35x72 = 2520

---

Relative Speed:

It is defined as the speed of a moving object with respect to another.

It mainly includes:

  Two bodies moving in the same direction

  Two bodies moving in the opposite direction

Relative Speed Formulas:

• When two objects are moving in the same direction, relative speed is given as their difference.

  If two objects are moving with speeds X and Y, their relative speed is X – Y, if they are moving in the same direction

• When the two objects are moving in opposite directions, relative speed is given by adding the two speeds.

  If two objects are moving with speeds X and Y, their relative speed is X + Y, if they are moving in the opposite direction

Time and Distance Formula

Distance = Speed × Time.

Speed is inversely proportional to the time taken when distance travelled is constant.

So, when speed increases, time decreases and vice versa.

Note:

There will be no change in the relative speed equation, if both the bodies reverse their direction at the same instant

The description of the motion of the two bodies between two consecutive meetings will also be governed by the proportionality between speed and distance – since the time of movement between any two meetings will be constant

Examples:

1. Two friends Jack and Jimmy 130 miles apart from each other, start travelling towards each other at the same time. If the Jack covers 7 miles per hour to the Jimmy’s 6 miles per hour, how far will Jimmy have travelled when they meet?

Solution: Time taken to meet = (Distance between them)/ (Relative speed)

Here moving in opposite direction

Relative speed = x + y = 7 + 6 = 13 miles per hour

Time taken to meet = 130/ 13 = 10 hours

Therefore, Jimmy travels = 10 x 6 = 60 miles

2. Two trains for station A leave station B at 8 am and 8.48 am and travel at 100 kmph and 145 kmph respectively. How many kilometres from station B will the two trains be together?

Solution:

Distance gained by first train started at 8 am till 8:48 am = 100*(48/60) = 80 km

Relative speed = 145 – 100 = 45

Time = relative distance / relative speed = 80/45 hours

distance travelled by first train = 80 + (80/ 45) *100 = 257.77 km

3. The distance between two hills P and Q is 65 km. A car racer starts from P towards Q at 6 am at a speed of 5 km/hr. Another car racer starts from Q towards P at 7 am at a speed of 15 km/hr. At what time will they cross each other?

Solution: In an hour, the earlier racer covers a distance of 5 km.

• The distance between the two = 65 – 5 = 60 km.
• Therefore, the two racers approach each other with a relative speed of 5 + 15 = 20 kmph.
• time taken = 60/ 20 = 3 hrs.
• So, they meet each other at (7 + 3) = 10 am.

4. Two cars start at the same time from X and Y and proceed towards each other at the rate of 20 km/hr and 24 km/hr respectively. When they meet, it is found that one car has travelled 80 km more than the other. The distance between the X and Y is

Solution:

Both the cars are coming closer to each other by (24 – 20) = 4 km/ hr.

They would meet after 80/4 = 20 hrs.

Hence, the distance between the X and Y = (24 + 20) x 20 = 44 x 20 = 880 km.

5. Two trains of length 300m and 500m run on parallel lines. when they run in the opposite direction, they take 20 sec to cross each other and when they run in same direction, they take 80 sec to cross each other. Find the speed of faster train.

Solution:

When they run in same direction relative speed = p – q

When they run in opposite direction relative speed = p + q

We know that (p – q) x 80 = (p + q) x 20

  80p – 80q = 20p + 20q

  60p = 100q

  3p = 5q – (1)

We know that (p – q) x 80 = 800 m

p – q = 10 – (2)

Solving 1 & 2

p – (3/5) p = 10

5p – 3p = 50

2p = 50

p = 25, q = 15

The speed of the faster train = 25 m/sec

---

A number series is a sequence of numbers written from left to right in a certain pattern. To solve the questions on series, we have to detect/find the pattern that is followed in the series between the consecutive terms, so that the wrong/missing term can be find out.

Types of Series

There can be following types of series 

 1. Prime Number Series:

The number which is divisible by 1 and itself, is called a prime number. The series formed by using prime number is called prime number series.

Example: Find out the next term in the series 7,11,13,17, 19....

Sol. Given series is a consecutive prime number series.

 Therefore, the next term will be 23

 2. Addition Series:

The series in which next term is obtained by adding a specific number to the previous term, is known as addition series.

Addition series are increasing order series and difference between consecutive term is equal.

Example: Find out the missing term in the series 2, 6, 10, 14, _, 22.

Solution: Here, every next term is obtained by adding 4 to the previous term.

So, Required term = 14 + 4 = 18

 3. Difference Series:

Difference series are decreasing order series in which next term is obtained by subtracting a fixed/specific number from the previous term.

Example: Find out the missing term in the series 108, 99, 90, 81, _, 63.

Solution: Here, every next number is 9 less than the previous number.

So, required number = 81 - 9 = 72

 4. Multiple Series:

When each term of a series is obtained by multiplying a number with the previous term, then the series is called a multiplication series.

Note: Number which is multiplied to consecutive terms, can be fixed or variable

Example: Find out the missing term in the series 4, 8,16, 32, 64, _, 256.

Solution: Here, every next number is double the previous number.

So, required number = 64 x 2 = 128

 5. Division Series:

 Division series are those in which the next term is obtained by dividing the previous term by a number.

Note Number which divides consecutive terms can be fixed or variable

Example: Find out the missing term in the series 10080,1440, 240, _, 12,4

Series pattern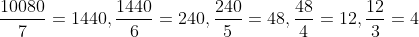 

Hence, missing term is 48

 6. n² Series

When a number is multiplied with itself, then it is called as square of a number and the series formed by square of numbers is called n² series.

Example: Find out the missing term in the series 4,16, 36, 64, _, 144.

Solution: This is a series of squares of consecutive even numbers.

Let us see 2² = 4, 4² = 16, 6² = 36, 8² = 64, 10² = 100, 12² = 144

Hence, missing term is 100

 7. (n² + 1) Series

If in a series each term is a sum of a square term and 1, then this series is called (n² +1) series. Example: Find out the missing term in the series 10, 17, 26, 37, _, 65.

Solution: Series pattern 3² + 1 = 10, 4² + 1 = 17, 5² + 1 = 26, 6² + 1 = 37, 7² + 1 = 50, 8² + 1 = 65

 So, required number = 50

 8. (n² - 1) Series

In a series, if each term is obtained by subtracting 1 from square of a number, then such series    is known as (n² -1) series.

Example: Find out the missing term in the series 0, 3, 8,15, 24, _, 48.

Solution: Series pattern 1² - 1 = 0, 2² - 1 = 3, 3² - 1 = 8, 4² - 1 = 15, 5² - 1 = 24, 6² - 1 = 35, 7² - 1 = 48

So, correct answer is 35.

 9. (n² + n) Series

Those series in which each term is a sum of a number with square of that number, is called as (n² + n) series.

Example: Find out the missing term in the series 12, 20, 30, 42, _, 72.

Solution: Series pattern 3² + 3, 4² + 4, 5² + 5, 6² + 6, 7² + 7, 8² + 8

So, required number =7² + 7 = 56

 10. (n² - n) Series

Series in which each term is obtained by subtracting a number from square of that number, is known as (n² - n) series.

Example: Find out the missing term in the series 42, 30,_,12, 6.

Solution: Series pattern 7² - 7, 6² - 6, 5² - 5, 4² - 4, 3² - 3

So, required number = 5² - 5 = 20

 11. n³ Series

A number when multiplied with itself twice, then the resulting number is called the cube of a number and series which consist of cube of different number following a specified sequence, is called as n³ series.

Example: Find out the missing term in the series 1, 8, 27, _, 125, 216.

Solution: Series pattern 1³, 2³, 3³, 4³, 5³, 6³

 So, required number = 4³ = 64

 12. (n³ + 1) Series

Those series in which each term is a sum of a cube of a number and 1, are known as (n³ +1) series.

Example: Find out the missing term in the series 126, 217, 344, _, 730.

Solution: Series pattern 5³ + 1, 6³ + 1, 7³ + 1, 8³ + 1, 9³ + 1 So, required number = 8³ + 1 = 513

 13. (n³ - 1) Series

 Series in which each term is obtained by subtracting 1 from the cube of a number, is known as (n³ -1) series.

Example: Find out the missing term in the series 0, 7, 26, 63, 124, 215, ....

Solution: Series pattern 1³ – 1, 2³ - 1, 3³ - 1, 4³ - 1, 5³ – 1, 6³ - 1, 7³ - 1

So, required number = 7³ - 1 = 342

 14. (n³ + n) Series

When each term of a series is a sum of a number with its cube, then the series is known as (n³ + n) series.

Example: Find out the missing term in the series 2,10, 30, ..., 130, 222.

Solution: Series pattern 1³ + 1, 2³ + 2, 3³ + 3, 4³ + 4, 5³ + 5, 6³ + 6

 So, required number = 4³ + 4 = 68

 15. (n³ - n) Series

When each term of a series is a sum of a number with its cube, then the series is known as (n³ + n) series.

Example: Find out the missing term in the series 2,10, 30, ..., 130, 222.

Solution: Series pattern 1³ + 1, 2³ + 2, 3³ + 3, 4³ + 4, 5³ + 5, 6³ + 6

So, required number = 4³ + 4 = 68

 16. Alternating Series

In alternating series, successive terms increase and decrease alternately.

The possibilities of alternating series are if it is a combination of two different series.

Two different operations are performed on successive terms alternately.

Example: Find the next term in the series 15,14,19,11,23,8, ...

Series Pattern

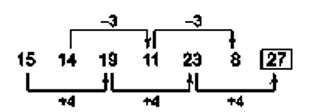
 17.  Arithmetic Progression (AP)

The progression of the form a, a + d, a + 2d, a + 3d, ...is known as an arithmetic progression with first term a and common difference d.

Then, nth term T_n = a + (n -1) d

Example: In series 359, 365, 371..., what will be the 10th term?

Solution:

The given series is in the form of AP.

Since, common difference i. e., d is same.

Here, a = 359 and d = 6

10th term = a + (n - 1) d= 359 + (10 - 1) 6= 359 + (9 x 6) = 413.

 18.  Geometric Progression (GP)

The progression of the form a, ar, ar², ar³... is known as a GP with first term a and common ratio = r.

Then, nth term of GP T_n = ar^n-1

Example: In the series 7,14, 28…..., what will be the 10th term?

Solution: The given series is in the form of GP.

 Since, common ration i. e., r is same.

Here, a = 7 and r = 2, 10th term = ar^n-1 = 7(2)^10-1 = 7 x 2⁹ = 3584

Examples:

 1.  4, 8, 24, 60, 124, ?

Solution: 

Series pattern

 4 + 2² =8

 8 + 4² = 24

24 + 6² = 60

60 + 8² = 124

124 + 10² =224

So, number is 224

 2.  8, 12, 24, 46, 72, 108, 52. which one is odd man out?

Solution: 8 + 4 = 12

12 + 12 = 24

24 + 20 = 44

should come in place of 46

44 + 28 = 72

72+ 36 = 108

108 + 44 = 152

So, 44 should come in place of 46

3. 13, 25, 40, 57, 79, 103, 130. What one is odd man out?

Solution:

Series pattern

 13 + 12 = 25

 25+ 15 = 40

40 + 18 = 58

should come in place of 57

58 + 21 = 79

79 + 24 = 103

103 + 27 = 130

4. 13, 35, 57, 79, 911, ?

Solution:

Series pattern

The elements of the given series are the numbers formed by joining together consecutive odd numbers in order, i.e., 1 and 3, 3 and 5, 5 and 7, 7 and 9, 9 and 11, ...

Therefore, Missing term = Number formed by joining 11 and 13 = 1113

5. 7, 9, 16, 25, 41, 68, 107, 173

Solution:

Series pattern

 7+9 = 16;

9 + 16=25;

16 + 25 = 41;

25 + 41 = 66;

Should come in place of 68

41 + 66 = 107;

 66 + 107 = 173

Clearly, 68 is wrong and will be replaced by 66.

---

Last two digits of a number is generally the tens place and units place digit of that number.

Let the number be 1345, the last two digits of this number are 4 and 5.

Method to calculate last two digits of a product:

Let us take the product of two numbers P and Q (Let us take P is 1448 and Q is 2677).

Let u and v, respectively represent the digits in the ten’s place and one’s place of P and same way x and y respectively represent the digits in the ten’s place and one’s place of Q, then

1. Unit’s digit of P x Q is given by the unit’s digit in the product of v and y results in more than 1-digit, excess digit will be carried over to the left. i.e., in 1448 x 2677, multiply 8 and 7 giving 56. So, 6 is unit’s digit and 5 goes as carry to step 2
2. Next, we cross multiply u and y & x and v, then add the resulting products. i.e., in 1448 x 2677 => 4 x 7 + 8 x 7 = 28 + 56 = 84
3. If a carry is generated in step 1, add that with the result obtained in step 2. i.e., 5 + 84 = 89
4. The unit’s digit in the result obtained in step 3 forms the tens digit in the product of P and Q i.e., the units digit in 89 which is 9 becomes the tens digit of 1448 x 2677.

So, the last two digits of 1448 x 2677 is 9 and 6

Before finding last two digits, let us see the binomial theorem for calculations

(x + a) ⁿ = ⁿC₀ aⁿ + ⁿC₁ a^{n – 1} x + ⁿC₂ a^{n – 2} x² + …... where ⁿC_r

Method of finding last two digits:

Let the number be in the form p ^q

Last two digits of numbers ending in 1

If p ends in 1, then p raised to q, ends in 1 and its digit is obtained by multiplying the tens digit in p with the unit’s digit in q.

Example: find the last two digits of 81²³⁶

Solution: Since the base 81 ends in 1, 81²³⁶ ends in 1 and the tens place digit is obtained from the unit’s digit in 8 x 6 which is 8. Hence the last two digits of 81²³⁶ are 8 and 1.

Last two digits of numbers ending in 3, 7 or 9

Convert the number by repeatedly squaring until we get the unit digit as 1, and then apply the same process of finding the last two digits of number with unit digit 1.

Alternative way:

1. When p ends in 9 raised to the power q.

• Raise the base divide the exponent by 2
• We know that number ending in 9 and raised to the power 2 ends in 1
• As the base now ends in ‘1’ we can follow the method of finding last two digits of numbers ending in 1.

2. When p ends in 3 raised to the power q.

• Raise the base divide the exponent by 4
• We know that number ending in 3 and raised to the power 4 ends in 1
• As the base now ends in ‘1’ we can follow the method of finding last two digits of numbers ending in 1.

3. When p ends in 7 raised to the power q.

• Raise the base divide the exponent by 4
• We know that number ending in 7 and raised to the power 4 ends in 1
• As the base now ends in 1 we can follow the method of finding last two digits of numbers ending in 1.

Last two digits of numbers ending in 2, 4, 6 or 8

When p ends with the even numbers, we can find the last two digits of the number raised to the power q by this method

We know that 2¹⁰ = 24

• (24) ^{odd number} always ends in 24
• (24) ^{even number} always ends in 76
• (76) ^number always ends in 76

Let us see an example:

2³⁶ = 2³⁰ x 2⁶

      = (2¹⁰)³ x 2⁶

      = 24³ x 2⁶

     = 24 x 64 (since 24^oddnumber always ends in 24)

    = 36(last two digits)

Last two digits of numbers ending in 0 or 5

• When any number with its unit digit as 0 raised to any power gives 00 in last two digits.
• When p ends with the 5, we can find the last two digits of the number raised to the power q by this method

Example: (65)²⁶⁵

Here ten’s digit of base is even and exponent is odd, last two digits of (65)²⁶⁵ is 2 and 5.

Examples:

1. Find the last two digits of 51³⁵

Solution: ending with 1

The unit digit is 1 itself

In the last two digits ten’s digit is given by taking product of ten’s digit in base and units digit in component i.e., 5 x 5 = 25

So, take 5 as ten’s digit

So, the last two digits are 51 

2. Find the last two digits of 17¹⁸⁰

Solution: 17¹⁸⁰ = (17²)⁹⁰

                           = (89)⁹⁰ [last two digits of 17²]

                        = (21)⁴⁵ [last two digits of 89²]

Here base is ending with 1

Ten’s digit of base is 2 and unit’s digit of power is 5.

 2 x 5 = 10 or 0

Therefore, last two digits of 17¹⁸⁰ = 01

3. Find the last two digits of 145¹⁵⁷

Solution: here ten’s digit of base is even and exponent is odd

So, last two digits of 145¹⁵⁷ will be 25

4. Find the last two digits of 82⁴⁴

Solution: 82⁴⁴ can be written as 2⁴⁴ x 41⁴⁴

2⁴⁴ = (2¹⁰)⁴ x 2⁴ = 24⁴ x 16 = 76 x 16 = 16

Base is 1: 41⁴⁴

4 x 4 = 16

So last two digits are 61

Therefore, last two digits of 82⁴⁴ are 16 x 61 = 76

---

Number of factors of a number:

If a number N can be represented as  where P₁, P₂, P₃ are prime factors of N then number of factors of N can be found as (a + 1) * (b + 1) * (c + 1).

50 = 2 * 5², so number of factors of 50 = (1+1) * (2+1) =6. Which are 1, 2, 5, 10, 25and 50.

These are various combinations of the prime factors 2, 5 and 5.

• Take 544; By using the divisibility rules we can easily see 2, 4, 8 are factors of 544. Take the highest power of each prime (here 8) for division.

544/8 = 68, divisible by 2, 4 and 17.

Take the highest power of each prime

68/ (4 * 17) = 1.

544 = 8 * 4 * 17 = 2⁵ * 17

Number of factors = 6 * 2 = 12

• Take 1080; Applying divisibility rules, we get 2, 3, 4, 5, 8, 9 divides the number. Take the highest power of each prime (here 8, 5, 9) for division.

1080 / (8 * 5 * 9) = 3 (can stop dividing here as we got a prime, no need to write an obvious step to get unity by dividing with the same prime!)

1080 = 8 * 5 * 9 * 3 = 2³* 3³* 5

Number of factors = (3 + 1) * (3 + 1) * (1 + 1) = 4 * 4 * 2 = 32

Sum of factors of a number

Let’s take an example:  40 = 2³ * 5,

number of factors = (3 + 1) * (1 + 1) = 4 * 2 = 8.

Sum of the factors = 1 + 2 + 4 + 8 + 5 + 10 + 20 + 40 = 90

This is same as (2⁰ + 2¹ + 2² + 2³) (5⁰ + 5¹) = 15 * 6 = 90.

• Find the sum of all the powers of each prime numbers, starting from 0 to the highest power contained in the standard form. Product of all such sums will give us the sum of the factors.
• We have already seen that 1080 = 2³ * 3³ * 5
• In this case, sum of the factors will be (2⁰ + 2¹ + 2² + 2³) * (3⁰ + 3¹ + 3² + 3³) * (5⁰ + 5¹) = 15 * 40 * 6 = 3600

This also explains how we find the numbers of factors. It is the product of the number of factors in each bracket (here, 4 * 4 * 2 = 32).

Product of factors of a number

N = 

Then the product of all the factors of N = N ^{(a + 1) (b + 1) (c + 1)/2}

e.g., 50 = 2 * 5²;

Product of all factors of 50 = 50 ^{(6) / 2} = 50³

Number of odd factors

• To get the number of odd factors, ignore the powers of 2.
• Take 1080, 1080 = 2³ * 3³ * 5
• Number of odd factors of 1080 = (3 + 1) * (1 + 1) = 4 * 2 = 8, here we considered only the powers of 3 and 5 to get the number of odd factors.

Sum of odd factors of a number

• Sum of factors of 1080 = (2⁰ + 2¹+ 2²+ 2³) * (3⁰+ 3¹+ 3²+ 3³) * (5⁰+ 5¹), where each term in the expansion represents a factor of 1080.
• We need at least one 2 to get an even factor.  Remove all terms that has a 2 in it and we will remove all even factors.
•  Even factors in 1080 are 2¹, 2²and 2³.
• The only power of 2 remaining is 2⁰ (=1), which can be removed as it will not make any impact. Means, you ignore all powers of 2 to get the sum of all odd factors.
• Now we need to remove even factors from the expression so that the result will be the sum of all odd factors.
• Sum of odd factors of 1080 = (3⁰+ 3¹+ 3²+ 3³) * (5⁰+ 5¹) = 240

Number of even factors of a number

Let a number is of the form, N = 2^a x   ...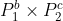

• Then Number of even factors of N = a * (b + 1) * (c + 1) …

For e.g., 1080 = 2³ * 3³ * 5

Number of even factors of 1080 = 3 * (3 + 1) * (1 + 1) = 24

Sum of even factors of a number

• To get the sum of the even factors we need to ensure that all the terms in the expression for the sum of factors are even.
• All members in the 2’s bracket except 2⁰ will give an even number.
•  Remove 2⁰ from the group and that’s all it takes!

For e.g., 1080 = 2³ * 3³ * 5

Sum of even factors of 1080 = (2¹ + 2² + 2³) * (3⁰ + 3¹ + 3² + 3³) * (5⁰ + 5¹) = 3360

Other conditions

What if we are asked to find the sum and number of factors of 1080 which are divisible by 15?

• We don’t have to use anything else other than the logic we used for odd and even factors. We know number of terms in the expression is the number of factors.
• So, when a condition is given, number of factors is the number of terms in the expression satisfying the given condition and considers only those factors to get the sum.
• 1080 = (2⁰ + 2¹+ 2²+ 2³) * (3⁰+ 3¹+ 3²+ 3³) * (5⁰+ 5¹)
• Now 15 = 3 * 5, so we need to ensure that every term in the expression has a 3 and 5 in it. Now look at the bracket of 3 and find the terms that don’t yield a 3 in the expression.

Also check for bracket of 5 for the terms that don’t give us a 5. 3⁰and 5⁰are the culprits. Remove those entries and we get the expression we need.

Examples:

1. Find Sum of factors of 1080 which are divisible by 15

 = (2⁰ + 2¹+ 2²+ 2³) * (3¹+ 3²+ 3³) * (5¹)

= 15 * 39 * 5 = 2730

  2. Find the sum of factors of 544 which are perfect squares

• 544 = 8 * 4 * 17 = 2⁵ * 17
• Our expression, (2⁰+ 2¹+ 2²+ 2³+2⁴ +2⁵) (17⁰+17¹)
  Ensure all terms in the expression satisfy the condition, perfect squares.
• So, each term in the expression should be of even power. We have to remove all odd powers in the expression

• Required sum is (2⁰+ 2² +2⁴) (17⁰) = 21.
• Number of factors = 3 * 1 (number of terms in each bracket) = 3.

3. For the number 1000 find the below values

• The number of divisors = (3 + 1) * (3 + 1) = 16 (as 1000 = 2³* 5³)
• The product of divisors = 1000^16/2 = 1000⁸
• The sum of divisors= (2⁰+ 2¹+ 2²+ 2³) (5⁰ + 5¹+ 5²+ 5³) = 2340
• The sum and number of odd divisors

we need to remove all factors that can yield a 2 from the two’s bracket.

Sum of odd factors = (2⁰) * (5⁰+ 5¹+ 5²+ 5³) = 156

Number of odd factors = 1 * 4 = 4

• The sum and number of even divisors

We need to remove all factors that cannot yield a 2 from the two’s bracket (which is 2⁰)

Sum of even factors = (2¹+ 2²+ 2³) (5⁰+ 5¹+ 5²+ 5³) = 2184

Number of even factors = 3 * 4 = 12

• The sum and number of divisors which are perfect squares

We need to remove all the factors which are not perfect squares

Sum of factors which are perfect squares = (2⁰+ 2²) (5⁰+ 5²) = 130

Number of factors which are perfect squares = 2 * 2 = 4

• The sum and number of divisors which are not perfect squares

Total sum – sum of divisors which are perfect squares = 2340 – 130 = 2210

Total factors – number of divisors which are perfect squares = 16 – 4 = 12

• The sum and number of divisors which are divisible by 125

We need to remove all the factors that cannot yield 125 (125 = 5³)

Sum of factors which are divisible by 125 = (2⁰+ 2¹+ 2²+ 2³) (5³) = 1875

Number of factors which are divisible by 125 = 4 * 1 = 4

• The sum and number of divisors which are divisible by 100

100 = 2² * 5²

We need to remove all factors that cannot yield a 2² from two’s bracket and also remove all factors that cannot yield a 5² from five’s bracket.

Sum of factors which are divisible by 100 = (2²+ 2³) (5²+ 5³) = 1800

Number of factors which are divisible by 125 = 2 * 2 = 4

---

A quadratic equation is an equation in which the highest power of an unknown quantity is a square that can be written as ax² + bx + c = 0 where, a and b are coefficients of x² and x, respectively and c is a constant.

The factor that identifies this expression as quadratic is the exponent 2. The coefficient of x² i.e., a cannot be zero, (a≠0)

To check whether an equation is quadratic or not, following examples will help to understand it in a better way.

1. 5x³ – 4x + 5 = 0 is not a quadratic equation because here the first term is raised to the 3^rd power. It must be raised to the 2^nd power in order to be quadratic.
2. 7x² – 6x + 2 = 0 is a quadratic equation, which is in the correct form i.e., ax² + bx + c = 0
3. 9x² = 81 is a quadratic equation, here it can be written as 9x² – 81 = 0 where a = 9, b = 0, c = - 81

Note:

1. A quadratic equation has two and only two roots.
2.  If a be the root of the quadratic equation ax² + bx + c = 0, then (x - a) is a factor of ax² + bx + c=0

Important Points Related to Quadratic Equations:

1.  A quadratic equation ax² + bx + c = 0 has

• • two distinct real roots, if D > 0.
  •   two equal real roots, if D = 0.
  •  no real roots, if D < 0.
  •  reciprocal roots, if a=c.
  • one root = 0, if c = 0.
  •  negative and reciprocal roots, if c = - a.
  •  both roots equal to 0, if fa = 0, c = 0 where, discriminant (D) = b² - 4ac

2. Formation of Quadratic Equation Let p and q be two roots. Then, we can form a quadratic equation as

• • •  x² – (sum of roots) x + (product of roots) = 0
    • x² – (p + q) x + (pq) = 0

=> (x – p) (x – q) = 0

• Here, for standard quadratic equation ax² + bx + c = 0, 

Examples:

1. In solving a problem, one student makes a mistake in the coefficient of the first-degree term and obtains - 9 and - 1 for the roots. Another student makes a mistake in the constant term of the equation and obtains 8 and 2 for the roots. The correct equation was

Solution:

• When mistake is done in first degree term, the roots of the equation are - 9 and - 1.
• So, equation is (x + 1) (x + 9) = x² + 10x + 9 ...(i)
• When mistake is done in constant term, the roots of equation are 8 and 2.
•  Therefore, Equation is (x - 2) (x - 8) = x² - 10x + 16 ...(ii).
•  Required equation from Eqs. (i) and (ii) is = x² - 10x + 9
• Also, we see in both the cases 1 st degree term is same with opposite sign i. e., in such questions we should take data from given conditions and find the correct equation

2. Two numbers whose sum is 8 and difference is 4, are the roots of the equation, find the equation?

Solution: Let the roots be p and q.

Given p + q = 8 – (1)

p – q = 4 – (2)

By solving 1 and 2, we get p = 6 and q = 2

Therefore, required equation is x² – (p + q) x + pq = 0

                                                    x² – (8) x +12 = 0

  3. If one of the roots of quadratic equation 7x² - 50x + k = 0 is 7, then what is the value of k?

Solution: Given equation is 7x² – 50x + k = 0.

Here, a = 7, b = - 50, c = k

  4. The sum of the roots of the equation 5x + (p + q + r) x + pqr = 0 is equal to zero. What is the value of (p³ + q³ + r³)?

Solution: Given equation, 5x + (p + q + r) x + pqr = 0

Here a = 5, b = p + q + r and c = pqr

According to the formula, a³ + b³ + c³ = 3abc, if a + b + c = 0

From this p³ + q³ + r³ = 3pqr

---

The mathematical expressions in which both sides are not equal are called inequalities.

In inequality, unlike in equations, we compare two values where the equal to sign in between is replaced by <, > and ≠ sign.

• a < b → a is less a than b
• a > b → a is greater than b
• a ≠ b → a is not equal to b
• a ≤ b → a is less than or equal to b
• a ≥ b → a is greater than or equal to b

Rules of inequalities:

Rule1:

• If, a < b and b < c, then a < b
• If, a > b and b > c, then a > b

Rule2:

• If, a > b, then b < a
• If, a < b, then b > a

Rule3:

• If a < b, then a − c < b – c and a + c < b + c
• If a > b, then a + c > b + c and a − c > b – c

Rule4:

• If a < b, and c is positive, then ac < bc
• If a < b, and c is negative, then ac > bc (inequality swaps)

Rule5:

Having minus in front of a and b changes the direction of the inequality.

• If a < b then −a > −b
• If a > b, then −a < −b 

Rule6:

The reciprocal of both a and b changes the direction of the inequality.

When a and b are both positive or both negative.

• If a < b, then 1/a > 1/b
• If a > b, then 1/a < 1/b

Rule7:

Taking a square root will not change the inequality.

• If a ≤ b, then 

Solving inequalities:

To solve an inequality, the following steps:

• Eliminate fractions
• Simplify
• Add or subtract quantities

Important points:

• Inequalities can be solved by adding, subtracting, multiplying, or dividing both sides by the same number.
• Do not multiply or divide by a variable.
• Dividing or multiplying both sides by negative numbers will alter the inequality's direction.

 

1. Absolute value inequalities:

It is an inequality with an absolute value symbol in it and can be solved by two methods.

• Using number line
• Using formulae

The absolute value inequalities are of two types:

• one with < or ≤
• one with > or ≥

 Formulae

1. When the inequality is in the form |x|< a or |x|≤ a

Formulae to solve the inequality:

If |x|< a => -a < x < a

If |x|≤ a => -a ≤ x ≤ a

2. When the inequality is in the form |x|> a or |x|≥ a

Formulae to solve the inequality:

If |x|> a => x < - a or x > a

If |x|≥ a => x ≤ - a or x ≥ a

3. When the inequality is in the form |x|< - a or |x|≤ - a

|x|< −a or |x|≤ −a ⇒ No Solution

4. When the inequality is in the form |x|> - a or |x|≥ - a

|x|> −a or |x|≥ −a ⇒ Set of all Real Numbers, R

 2. Quadratic Inequalities:

The standard form of quadratic inequalities in one variable is almost the same as the standard form of a quadratic equation.

The only difference is that the quadratic equation has an "equal to" sign in it while a quadratic inequality has a "greater than" or "less than" sign (> or <).

The quadratic inequality is represented as: ax² + bx + c > 0 or ax² + bx + c < 0

Quadratic inequality can have infinite values of x which satisfy the condition ax²+ bx +c<0 ax²+ bx + c <0.

Now consider a quadratic expression x² + bx + c. We can write the quadratic expression in the form of (x−α) (x−β) and α < β.

By number line method

It means that if x² + bx + c, then x can take values between -  to α and β to + 

• If x² + bx + c, then x ? (- , α) ∪ (β, + )
• If x² + bx + c, then x can take values between α and β.
• If x² + bx + c, then x ? (α, β)

Symbols used inequalities:

(-1, 1) -> x cannot take value -1 and 1.

[-1, 1) -> x can take value -1 and but not 1.

(-1,1] -> x cannot take value -1 but it can take value 1.

[-1, 1] -> x can take both -1 and 1 values

1. Linear Inequalities:

Linear inequalities are defined as expressions in which two linear expressions are compared using the inequality symbols.

Rules of Linear Inequalities:

Four types of operations that are done on linear inequalities are addition, subtraction, multiplication, and division.

Addition Rule:

If a > b, then a + c > b + c

if a < b, then a + c < b + c.

Subtraction Rule:

If a > b, then a − c > b – c

if a < b, then a – c < b − c.

Multiplication Rule:

If a > b and c > 0, then a × c > b × c

If a < b and c > 0, then a × c < b × c,

If a > b and c < 0, then a × c < b × c

If a < b and c < 0, then a × c > b × c.

Division Rule:

If a > b and c > 0, then (a/c) > (b/c)

If a < b and c > 0, then (a/c) < (b/c)

If a > b and c < 0, then (a/c) < (b/c)

If a < b and c < 0, then (a/c) > (b/c)

Examples:

• 1. What is the scope of (x -1) (x + 5)/ (x + 3) < x?

Solution:

For inequalities, if you multiply both sides by (x + 3)² the squared number is always positive, so the inequality sign doesn’t change.

Thus, you get (x + 3)² ((x -1) (x + 5)/ (x + 3)) < x (x + 3)²

(x + 3) (x - 1) (x + 5) = (x + 3)² x

(x + 3) (x - 1) (x + 5) - (x + 3)² x < 0

(x + 3) {(x - 1) (x + 5) - (x + 3) x} < 0

(x + 3) {(x² + 4x – 5) - (x² + 3x)} < 0

(x + 3) {x - 5} < 0

- 3 < x < 5

 2.  If  is not a real number, what is the scope of x?

Solution:

• If a certain polynomial is “not a real number” or “not defined”, the denominator must be 0 or the number inside the” √” root must be negative.
• Then, this question also has to be -4x² + 16 ≤ 0, and if you divide both sides by -4, from x² – 4 ≥ 0, (x – 2) (x + 2) ≥ 0,
•  x ≤ -2 or 2 ≤ x.

 3. Solve the linear inequality in one variable: 10x + 5 < 8x + 25

Solution:

Given inequality 10x + 5 < 8x + 25

10x + 5 – 8x < 8x + 25 – 8x

2x + 5 < 25

2x < 25 - 5

2x < 20

x < 10

• 3. A gardener is shaping a plant. In order to get the exact shape, it needs 350 millimetres wide, allowing for a margin of error of 5.5 millimetres. Find the range of width of the plant using absolute value inequality.

Solution: Let the width of the plant to be x.

Then the absolute value inequality is |x−350|≤ 5.5

−5.5 ≤ x − 350 ≤ 5.5

344.5 ≤ x ≤ 355.5

The range of the plant’s width [344.5, 355.5]

 5. Find the solution of the inequalities 10x + 12 >52 and 6x + 18 < 72.

Solution: Given 10x + 12 >52 and 6x + 18 < 72

10x > 52 – 12 and 6x < 72 – 18

10x > 40 and 6x < 54

x > 4 and x < 9

 

---

Exponent:

It is a numerical notation that indicates the number of times a number is to be multiplied by itself.

It is also called as power or index.

It is used to write a very big number in the simplest form.

Example: 10000 = 10⁴

Suppose, a number ‘p’ is multiplied by itself k-times, then it is represented as p^k where p is the base and k are the exponent.

In the number 6⁴, 6 is called as base and 4 is called as exponent or power.

It is read as 6 raised to the power 4

Comparison using exponents:

• When two numbers in the standard form have same power of 10, then number with larger factor is greater

7.54 x 10²² < 8.432 x 10²⁴

• When two numbers in the standard form have same factor, then number with larger power of 10 is greater

7.54 x 10¹² > 7.54 x 10¹⁰

• When two numbers in the standard form have different factors and the different powers of 10, then the number with larger power of 10 is larger number

7.54 x 10¹² > 7.54 x 10¹⁰

Important points to remember:

• A positive number raised to an even or odd power always remains positive.
• A negative number raised to an odd power always remains negative.
• A negative number raised to an even power always turns to be positive.

In simple we can say that any number raised to an even power either remains positive or becomes positive and any number raised to odd power keeps the sign it starts with.

Exponents Rules:

1. Product Rule:

same base different power

          a^u x a^v = a^{u + v}

different base same power

          a^u x b^u = (a x b) ^u

Example: 2⁵ x 2⁶ = 2⁵⁺⁶ = 2¹¹

                 4² x 5² = (4 x 5)² = 20²

2. Quotient Rule:

same base different power

(a^u/ a^v) = a^{u – v}

different base same power

(a^u/ b^u) = (a/b) ^u

Example: 3⁵/ 3² = 3^{5 – 2} = 3³ = 27

               : 12³/ 6³ = 2³ = 8

3. Power Rule:

  4. Negative exponent rule:

a^-u = 1/a^u

Example: 3^-2 = 1/3²

  5. Zero rule:

a⁰ = 1

0^u = 0, for n > 0

Example: 5⁰ = 1

                  0³ = 0

  6. One rule:

b¹ = b

1^u = 1

Example: 5¹ = 5

                  1⁵ = 1

  7. Minus one rule:

---

 

It is a system of geometry, where the position of points on the plane is described by using an ordered pair of numbers.

 Rectangular Coordinate Axes

The lines XOX' and YOY' are mutually perpendicular to each other and they meet at point O which is called the origin.

 

Line XOX' represents X-axis and line YOY' represents Y-axis and together taken, they are called coordinate axes.

 

Any point in coordinate axis can be represented by specifying the position of x and y-coordinates

Quadrants

The X and Y-axes divide the cartesian plane into four regions referred to quadrants

• The coordinates of point O (origin) are taken as (0,0).
• The coordinates of any point on X-axis are of the form (x, 0).
• The coordinates of any point on Y-axis are of the form (0, y)

Formulae:

Distance Formula

Distance between Two Points If A (x₁, y₁) and B (x₂, y₂) are two points, then 

Distance of a Point from the Origin

The distance of a point A (x, y) from the origin O (0, 0) is given by 

Area of triangle

If A (x₁, y₁) B (x₂, y₂) and C (x₃, y₃) are three vertices of a Triangle ABC, then its area is given by

 Area of triangle  (x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂))

Collinearity of Three Points

Three points A (x₁, y₁) B (x₂, y₂) and C (x₃, y₃) are collinear, if

(i)   Area of triangle ABC is 0

(ii)   Slope of AB = Slope of BC = Slope of AC

(iii)   Distance between A and B + Distance between B and C = Distance between A and C

Centroid of a Triangle

 

Centroid is the point of intersection of all the three medians of a triangle. If A (x₁, y₁) B (x₂, y₂) and C (x₃, y₃) are the vertices of triangle ABC, then the coordinates of its centroid are

Circumcentre

The circumcentre of a triangle is the point of inter section of the perpendicular bisectors of its sides and is equidistance from all three vertices.

 

 If A (x₁, y₁) B (x₂, y₂) and C (x₃, y₃) are the vertices of triangles and O (x, y) is the circumcentre of triangle ABC, then OA = OB= OC

Incentre

The centre of the circle, which touches the sides of a triangle, is called its incentre.

 

 Incentre is the point of intersection of internal angle bisectors of triangle.

If A (x₁, y₁) B (x₂, y₂) and C (x₃, y₃) are the vertices of a triangle ABC such that BC = a, CA = b and AB = c, then coordinates of its incentre I are 

Section formulae

• Let A (x₁, y₁) B (x₂, y₂) be two points on the cartesian plane.
• Let point P (x, y) divides the line AB in the ratio of m: n internally.

If P divides AB externally, then 

If P is the mid-point of AB, then  

Basic Points Related to Straight Lines

1. General form of equation of straight line is ax + by + c = 0. Where, a, b and c are real constants and x and y are two unknowns.

2. The equation of a line having slope m and intersects at c on x-axis is y = mx + c.

 

3. Slope (gradient) of a line ax + by + c = 0, by = - ax – c

Comparing with y = mx + c, where m is slope, therefore m = tan θ = 

Slope of the line is always measured in anti-clockwise direction.

 

4. Point slope form A line in terms of coordinates of any two points on it, if (x₁, y₁) and (x₂, y₂) are coordinates of any two points on a line, then its slope is 

5. Two-point form a line the equation of a line passing through the points A (x₁, y₁) and B (x₂, y₂) is 

 

6. Condition of parallel lines

If the slopes of two lines i.e., m₁ and m₂ are equal then lines are parallel.

Equation of line parallel to ax + by + c = 0 is ax + by + q =

 

7. Condition of perpendicular lines

If the multiplication of slopes of two lines i.e., m₁ and m₂ is equal to -1 then lines are perpendicular.

m₁ x m₂ = -1

Equation of line perpendicular to ax + by + c = 0 is bx - ay + q =0

 

 8. Angle between the two lines 

 

9. Intercept form Equation of line L intersects at a and b on x and y-axes, respectively is 

 

10. Condition of concurrency of three lines:

Let the equation of three lines are a₁x + b₁y + c₁ = 0,

a₂x + b₂y + c₂ = 0, and a₃x + b₃y + c₃ = 0.

Then, three lines will be concurrent, if

Distance of a point from the line:

Let ax + by + c = 0 be any equation of line and P (x₁, y₁) be any point in space. Then the perpendicular Distance(d) of a point P from a line is given by 

 

12. The length of the perpendicular from the origin to the line ax + by + c = 0, is 

 

 13. Area of triangle by straight line ax + by + c = 0 where a ≠ 0 and b ≠ 0 with coordinate axes is 

 

 14. Distance between parallel lines ax + by + c = 0 and ax + by + d = 0 is equal to 

 

15. Area of trapezium, between two parallel lines and axes,

Area of trapezium ABCD = Area of OCD

Examples:

Find the area of triangle ABC, whose vertices are A (8, - 4), B (3, 6) and C (- 2, 4).

Solution: Here, A (8, - 4) so, x₁ = 8, y₁ = - 4

                        B (3, 6) so, x₂ = 3, y₂ = 6

 

                           C (-2, 4) so, x₃ = -2, y₃ = 4

Therefore, area of triangle ABC (x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂))

(8(6 – 4) + 3(4 – (- 4)) + (-2) (-4-6))

 (16 + 24 + 20)

= 30 sq units

If A (-2,1), B (2, 3) and C (-2, -4) are three points, then find the angle between AB and BC.

 

Solution: Let m₁ and m₂ be the slopes of line AB and BC, respectively.

 

Let θ be the angle between AB and BC

 

 3. In what ratio, the line made by joining the points A (- 4, - 3) and B (5,2) intersects x-axis?

Solution: We know that y-coordinate is zero on x-axis,

 

Given, y₁ = - 3, y₂ = 2

Therefore, 

 

2m – 3n = 0

 

 4. Coordinates of a point is (0, 1) and ordinate of another point is - 3. If distance between both the points is 5, then abscissa of second point is

Solution: Let abscissa be x.

So, (x – 0)² + (-3 -1)² = 5²

x² + 16 = 25

x² = 9

 5. Do the points (4, 3), (- 4, - 6) and (7, 9) form a triangle? If yes, then find the longest side of the triangle

Solution: Let P (4, 3), Q (-4, -6) and R (7, 9) are given points.

Since, the sum of 12.04 and 6.7 is greater than 18.6.

 

So, it will form a triangle, whose longest side is 18.6

 

---

Triangle:

A triangle is a three - sided closed plane figure which is formed by joining 3 non-collinear points.

• In figure A, B, C are three non-collinear points which forms ?ABC.
•  Now, in a ?ABC,

There are three vertices A, B and C,

Three sides AB, BC and AC and

three angles ∠A, ∠B and ∠C and sum of these three angles is 180°. i.e., ∠A+ ∠B + ∠C =180°

Types of Triangles:

1.  Equilateral triangle: A triangle having all sides equal is called an equilateral triangle. In this triangle each angle is congruent and is equal to 60°

 2. Scalene triangle: A triangle having all sides of different length is called a scalene triangle.

 3. Isosceles triangle: A triangle having two sides equal is called an isosceles triangle. In this triangle angles opposite to congruent sides are also equal.

 4.  Right angled triangle: A triangle one of whose angles measures 90° is called a right-angled triangle. In ?ABC, ∠B = 90°

 5.  Obtuse angled triangle: A triangle one of whose angles lies between 90° and 180° is called an obtuse angled triangle. In ?ABC, ∠A >90°

 6.  Acute angled triangle: A triangle whose each angle is less than 90° is called an acute angled triangle. In ?ABC, (∠A, ∠B, ∠C) < 90^o

Properties of Triangles:

1. Sum of two sides is always more than third side

2. Difference of two sides is always less than third side

3. Greater angle has greater side opposite to it and smaller angle has smaller side opposite to it

4. The exterior angle is equal to the sum of two interior angles not adjacent to it, ∠ACD = ∠BCE = ∠A+ ∠B

Congruency of Triangles

Two triangles are congruent if they satisfy the following conditions.

1. SSS congruency (Side - Side - Side): If the three sides of one triangle are equal to the corresponding three sides of another triangle, then two triangles are congruent.

• In ?ABC and ?PQR, AB = PQ, BC = QR and AC = PR, then ?ABC = PQR

 2.  SAS congruency (Side - Angle - Side): If two sides and the angle included between them are equal to the corresponding side and angle included of other triangle are equal, then the two triangles are congruent.

• In ?ABC and ?PQR, AB = PQ, BC = QR and ∠B = ∠Q, then ?ABC = ?PQR

 3.   ASA congruency (Angle - Side - Angle): If two angles and the side included between them are equal to the corresponding angles and side included of other triangle are equal, then two triangles are congruent.

• In ?ABC and ?PQR, ∠B = ∠Q, ∠C = ∠R and BC = QR then, ?ABC = ?PQR

 4.  AAS congruency (Angle - Angle - Side): If two angles and the side other than the included side of one triangle are equal to the corresponding angles and the side other than included side of other triangle are equal, then the two triangles are congruent.

• In ?ABC and ?PQR, ∠B = ∠Q, ∠C = ∠R and AC = PR then, ?ABC = ?PQR

 5.  RHS congruency (Right Angle-Hypotenuse-Side):

 If hypotenuse and one side of right-angled triangle are equal to hypotenuse and corresponding side of other triangle, then the two triangles are congruent.

• In ?ABC and ?PQR, BC =QR AC=PR and ∠B = ∠Q= 90°, then ?ABC = ?PQR

Similarity of Triangles

Two triangles are said to be similar if they satisfy the following conditions.

1.  AA similarity (Angle-Angle Similarity): If two angles of one triangle are equal to the two angles of the other triangle, then the two triangles are similar.
2.  SAS similarity (Side-Side-Side Similarity): If two sides of one triangle are proportional to the corresponding side of other triangle and the angle included by them are equal, then the two triangles are similar.
3. SSS similarity (Side-Angle-Side Similarity): If three sides of one triangle are proportional to the corresponding three sides of other triangle, then the two triangles are similar.

Properties of Similar Triangle:

1. Ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides
2.  Ratio of the areas of two similar triangles is equal to the ratio of the squares of corresponding altitudes and medians
3.  In two similar triangles ABC and PQR

Some Important Terms Related to Triangles:

Angle Bisector:

• It is the bisector of an angle contained in the vertex of a triangle.
• All the three angle bisectors of a triangle meet at a point called the incentre of the triangle.
• The incentre is the centre of a circle which can be perfectly inscribed in the triangle.

• In radius = JD = JE = JF
• 

In ,AD, BE and CF are angle bisectors and meet at incentre J.

 

 

Perpendicular Bisector:

• It is the line passing through the mid-point of the side of a triangle and perpendicular to it.
• All the three perpendicular bisectors of a triangle meet at a point called the circumcentre of the triangle.
• The circumcentre is the centre of a circle which can be perfectly circumscribed about the triangle.
• The circumradius = PC = QC = RC and ∠QCR = 2∠P.
• In PQR, the angle bisectors meet at circumcentre C.
• Also, D, E and F are the mid-points of OR, RP and PQ, respectively

Median:

• It is the line joining the mid-point of a side of a triangle with the vertex opposite to that side.
• All the three medians of a triangle meet at a point called the centroid of the triangle.
• They also intersect each other such that each median is split in the ratio of 1: 2 from the base side.
• In ,AD, BE and CF are the medians and meet at the centroid G. D, E, F are mid-points of BC, CA and AB, respectively.

 

Examples:

1. The angles of triangle are in the ratio 3:5:7. The triangle is

Solution: Let the angle measure (3x) °, (5x) ° and (7x) °

• Then, 3x + 5x + 7x = 180 => 15x = 180 => x = 12
• These angles are 36° ,60° and 84°
• Therefore, the triangle is acute angled

 2. The side AC of a ABC is extended to ‘D’ such that BC = CD. If ∠ACB is 70°, then what is ∠ADB equal to?

 

Solution: Let’s draw a figure from given data

• ∠ACB + ∠BCD = 180^o
• ∠BCD = 180^o – 70^o = 110^o

 

 

• In  BC = CD

 

∠CBD = ∠CDB…(i)

 

• Also, ∠BCD + ∠CBD + ∠CDB = 180^o

 

2∠CBD = 180^o - ∠BCD

 

∠CBD = 180^o – 110^o ð = 70^o

 

Therefore, ∠CDB = ∠ADB =  = 35^o

 

 

 3. ABC is a triangle right angled at A and a perpendicular AD is drawn on the hypotenuse BC. What is BC.AD equal to?

 

Solution:

 

 

• In case of a right-angled triangle, if we draw a perpendicular from the vertex containing right angle to the hypotenuse, we get three triangles, two smaller and one original and these three triangles are similar triangles. 

here ?ABC ~ ?ABD ~ ?ADC

Therefore, BC. AD = AB. AC

 4. In a ?ABC, ∠A = 90^o, ∠C = 55^o and  What is the value of ∠BAD?

 

 

Solution: Let’s draw a figure from the given data

In ?BAC, ∠B = 180^o – (90^o + 55^o) = 35^o

 

Now, in ?ADB, ∠ADB = 90^o

∠ADB + ∠DBA + ∠BAD = 180^o

∠BAD = 180^o – 90^o – 35^o = 55^o

 5. In a ?ABC, if ∠A = 115°, ∠C = 20° and D is a point on BC such that AD  BC and BD = 7 cm, then AD is of length

 

Solution:

Let us draw a figure from the data given

Given, In ?ABC, , ∠A = 115^o, ∠C = 20^o

 

∠B = 180^o – (115^o + 20^o) = 45^o

Now in  ?ABC,  = tan 45^o

 

AD = BD = 7 cm

---

 

• It is a plane figure bounded by four straight lines. It has four sides and four internal angles.
• The sum of the internal angles of a quadrilateral is equal to 360°.

 

Parallelogram

 

A quadrilateral in which the opposite sides are equal and parallel, is called a parallelogram. In a parallelogram,

(i)   The sum of any two adjacent interior angles is equal to 180°.

 

 ∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A =180°

(ii)   The opposite angles are equal in magnitudes ∠A = ∠C and ∠B = ∠D.

(iii)   line joining the mid-points of the adjacent sides of a quadrilateral form a parallelogram.

 

(i)   line joining the mid-points of the adjacent sides of a parallelogram is a parallelogram.

()   The parallelogram inscribed in a circle is a rectangle and circumscribed about a circle is a rhombus.

 

(i) AC² + BD² =2 (AB² + BC²)

 

Rhombus

A parallelogram in which all the sides are equal, is called a rhombus.

(i)   The opposite sides are parallel and all the sides are of equal lengths. AB = BC = CD = DA.

(ii)  The sum of any two adjacent interior angles is equal to 180°. 

 

∠A + ∠B = ∠B + ∠C = ∠C + ∠D = ∠D + ∠A = 180° 

(iii)  The opposite angles are equal in magnitudes, i.e., ∠A = ∠C and ∠B = ∠D.

(i)  The diagonals bisect each other at right angles and form four right angled triangles.

()   Area of the four right triangles ?AOB = ?BOC = ?COD = ?DOA and each equal  the area of the rhombus.

(i)   Figure formed by joining the mid-points of the adjacent sides of a rhombus is a rectangle. 

Rectangle

A parallelogram in which the adjacent sides are perpendicular to each other and opposite side are equal is called a rectangle.

(i)  The diagonals of a rectangle are of equal magnitudes and bisect each other i.e., AC = BD and OA = OB = OC = OD.

 

(i)   The figure formed by joining the mid-points of adjacent sides of a rectangle is a rhombus.

(ii)   The quadrilateral formed by joining the mid-points of intersection of the angle bisectors of a parallelogram is a rectangle.

Square

 

A parallelogram in which all the sides are equal and perpendicular to each other, is called a square.

(i)   The diagonals bisect each other at right angles and form four isosceles right-angled triangles.

 

(ii)   The diagonals of a square are of equal magnitudes i.e., AC = BD.

 

(iii)   The figure formed by joining the mid-points of adjacent sides of a square is a square.

 

Trapezium

It is a quadrilateral where only one pair of opposite sides are parallel.

 

ABCD is a trapezium as AB || DC.

(i)   If the non-parallel sides i.e., (AD and BC) are equal, then diagonals will also be equal to each other,

(ii)   Diagonals intersect each other in the ratio of lengths of parallel sides.

(iii)   line joining the mid-points of non-parallel sides is half the sum of parallel sides and is called the median.

Cyclic Quadrilateral:

 

A quadrilateral whose vertices are on the circumference of a circle, is called a cyclic quadrilateral. The opposite angles of a cyclic quadrilateral are supplementary, i.e.,  = 180°.

 

If the side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior opposite angle. i.e., ∠ADC = ∠CBE

 

Polygons:

A polygon is a closed plane figure bounded by straight lines.

 Convex polygon

A polygon in which none of its interior angles is more than 180° is called convex polygon.

Concave polygon

A polygon in which at least one angle is more than 180° is called concave polygon.

 Irregular polygon

 A polygon in which all the sides or angles are not of the same measure.

 Regular polygon

 A regular polygon has all its sides and angles equal.

(iii)   Each exterior angle of a regular polygon = 

(ii)   Each interior angle = 180 — Exterior angle.

 

(iii)   Sum of all interior angles = (2n -4) x 90°

 

(i)   Sum of all exterior angles =360°

 

()   Number of diagonals of polygon on n sides = 

Examples:

 

 1. The angles of a quadrilateral are in the ratios 3: 4: 5: 6. The smallest of these angles is

 

Solution:

 

Let the angles of the quadrilateral be (3x) °, (4x) °, (5x) ° and (6x) °.

 

Then, 3x + 4x + 5x + 6x = 360 => 18x = 360 => x = 20

 

Smallest angle = (3 x 20) ° = 60°

 

 2. In the give figure, AD || BC. Find the value of x.

Solution: Here, AD|| BC,

 3. If one angle of a parallelogram is 24° less than twice the smallest angle, then the largest angle of the parallelogram is

Solution: Let the smallest angle be x^o

Then, its adjacent angle = (2x – 24) ^o

Therefore, x + 2x – 24 = 180

ð 3x = 204

ð x = 68

Therefore, Largest angle = (2 x 68 – 24) ^o = (136 – 24) ^o = 112^o

 4. A quadrilateral ABCD is inscribed in a circle. If AB is parallel to CD and AC = BD, then the quadrilateral must be a

Solution:

The quadrilateral must be trapezium because a quadrilateral where only one pair of opposite sides are parallel (in this case AB || CD) is trapezium.

 

 5. In the given figure, ABCD is a parallelogram in which ∠BAD = 75° and ∠CBD = 60°. Then, ∠BDC is equal to

Solution: Given ∠C = ∠A = 75^o

Since opposite angles of parallelogram are equal

In ?ABCD, ∠CBD + ∠BDC + ∠BDC = 180^o

60^o + 75^o + ∠BDC = 180^o

135^o + ∠BDC = 180^o

∠BDC = 45^o 

---

 

Circle

A circle is a set of points which are equidistant from a given point.

The given point is known as the centre of that circle.

In the given figure O is the centre of circle and r is the radius of circle.

 

Chord

A line segment whose end points lie on the circle.

• AB is the chord in the given figure.
• The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
• AD = DB and OD  AB.

 

(i)   Equal chords of a circle are equidistant from the centre and vice-versa.

 

 

 

(ii)   Equal chords subtend equal angles at the centre and vice-versa

 

(iii)   In a circle or in congruent circles equal chords are made by equal arcs

 

(i)   If two chords AB and CD of a circle, intersect inside a circle (outside the circle when produced at point E) then, AE x BE = CE x DE

Secant

 

A line segment which intersects the circle at two distinct points, is called as secant.

 

 

In the given diagram PQ intersects circle at two points at A and B

 

Sector of Circle

The region enclosed by an arc of a circle and its two bounding radii is called a sector of the circle. Thus, in the adjoining figure, OABO is the sector of the circle C (o, r)

 

Segment of a Circle

A chord divides the circle into two regions. These two regions are called the segments of a circle.

 

In the figure, PSR is the major segment and PQR is minor segment. Angles made in the same segment are equal.

Angles and Central Angles

• The angle subtended at the centre by any two points on the circumference of the circle is called central angle.

(i)   Angle in a semi-circle is a right angle.

 

(ii)   The angle subtended by an arc at the centre of the circle is twice the angle subtended by the arc at any point on the remaining part of the circle.

 

Tangent:

A line segment which has one common point with circumference of a circle i.e., it touches only at one point is called as tangent of circle.

 

In the given figure PQ is tangent which touches the circle at point R.

(i)   Radius is always perpendicular to tangent.

 

(ii)   The length of two tangents drawn from the external point to the circle are equal.

 

(iii)   The angle which a chord makes with a tangent at its point of contact is equal to any angle in the alternate segment. ∠PTA = ∠ABT, where AT is the chord and PT is the tangent to the circle.

(i)   If PT is a tangent (with P being an external point and T being the point of contact) and PAB is a secant to circle (with A and B as the points, where the secant cuts the circle), then PT² =PA x PB.

Pair of Circle

 

(i)   (a) When two circles touch externally, then the distance between their centres is equal to the sum of their radii then, AB = AC + BC

(b) When two circles touch internally the distance between their centres is equal to the difference between their radii AB = AC - BC

(ii)   In a given pair of circles, there are two types of tangents. The direct tangents and the cross (or transverse) tangents. In the figure, AB and CD are the direct tangents and EH and GF are the transverse tangents.

 

When two circle of radii r₁ and r₂ have their centres at a distance d.

Examples:

 

 1. Two circles of same radius 5 cm, intersect each other at A and B. If AB = 8 cm, then the distance between the centres is

Solution:

Let’s draw a figure from given data.

 

Let O and P be the radius of two circles.

 

From the figure, on joining AO and AP.

In ?AOX, PX = 3 cm

 

Therefore, Distance between the centre = OX + PX = 3 + 3 = 6 cm

 

 2. In a ABC, O is its circumcentre and ∠BAC = 50°. The measure of ∠OBC is

Solution: The angle subtended by an arc at the centre of the circle is twice the angle subtended by the arc at any point on the remaining part of the circle.

∴ ∠BOC = 2 ∠BAC = 2 X 50° = 100°

Now, in BOC, OB = OC

 

Let ∠OBC = ∠OCB= x

Therefore, x + x + 100^o = 180^o

 2x = 80^o

x = 40^o

 

 3. Find x in the given figure

 

Solution: If two chords of a circle, intersect inside a circle (outside a circle) at any point.

Then, PA x PB = PC x PD

ð 6 x 15 = 5 (x + 5)

ð x + 5 = 18

ð x = 13 cm

 

 1. If a regular hexagon is inscribed in a circle of radius r, then find the perimeter of the hexagon?

Solution: Here, OA = OB = AB = r

Therefore, perimeter of hexagon = 6 x AB = 6r

 

 2. R and r are the radii of two circles (R > 1). If the distance between the centres of the two circles be ‘d’, then length of common tangent of two circles is

Solution: Let us draw a figure from given data

 

Let the common tangent of both circles is PQ.

 

 

 

 

 

---

1. In a right-angled triangle OAB, where ∠BOA = θ

 2. Trigonometrical Identities:

• sin² θ + cos² θ = 1
• 1 + tan² θ = sec² θ
• 1 + cot² θ = cosec²θ

 3. Angle of Elevation:

Suppose a man from a point O looks up at an object P, placed above the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of elevation of P as seen from O.

Therefore, Angle of elevation of P from O = ∠AOP

 4. Angle of Depression:

Suppose a man from a point O looks down at an object P, placed below the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of depression of P as seen from O.

Examples:

1. The angle of elevation of the sun, when the length of the shadow of a tree is  times the height of the tree, is

1. Solution:

• Let AB be the tree and AC be its shadow.
• Let ∠ACB = 0
• 
• θ = 30^o

 2. The top of a 15-metre-high tower makes an angle of elevation of 60^o with the bottom of an electric pole and angle of elevation of 30^o with the top of the pole. What is the height of the electric pole?

Solution:

Let AB be the tower and CD be the electric pole.

Then, ∠ACB= 60^o, ∠EDB= 60^o and AB = 15m

Let CD = h. Then, BE = (AB – AE) = (AB – CD) = (15 – h)

 3. A ladder leaning against a wall makes an angle of 60⁰ with the ground. If the length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.

Solution: Let AB be the wall and BC be the ladder.

Then, ∠ACB = 60⁰ and BC = 19 m

Let AC = x metres

Therefore, distance of the foot of the ladder from the wall = 9.5 m

 4. A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30⁰ with the man’s eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60^o. What is the distance between the base of the tower and the point P?

Solution: Let us draw a figure from given data.

• Here one of the AB, AD and CD must have given.
• So, the data is inadequate.

 5. Two ships are sailing in the sea on he to sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed rom the ships are 30^o and 45⁰ respectively. If the lighthouse is 100 m high, the distance between the two ships is:

Solution:

Let us draw a figure from given data

Let AB be the light house and C and D be the positions of the ships.

Then, AB = 100 m, ∠ACB = 30⁰ and ∠ADB = 45⁰

---

Two triangles are said to be similar if they have equal pair of corresponding angles and same ratio of corresponding sides.

They have same shape but their sizes are different.

Similar triangles are denoted by ~

In the above figure, these two triangles are said to be similar only if

1. ∠A = ∠D, ∠B = ∠E and ∠C = ∠F
2. 

Properties of similar triangles:

1. Each pair of corresponding angles are equal
2. The ratio of corresponding sides is same
3. Both have same shape but sizes may be different

Similar triangles theorems:

Angle-Angle Similarity

Two triangles are said to be similar if any two angles of a triangle are equal to any two angles of another triangle.

In the above figure, if ∠A = ∠D and ∠B = ∠E then ΔABC ~ ΔDEF

Side-Angle-Side Similarity

If two sides of a triangle are proportional to the corresponding sides of another triangle, and the angle included by them in both the triangle are equal, then two triangles are said to be similar.

Thus, if ∠A = ∠D and AB/DE = AC/DF then ΔABC ~ΔDEF.

 From the congruency, AB/DE = BC/EF = AC/DF and ∠B = ∠E and ∠C = ∠F

Side-Side-Side Similarity

If all the three sides of a triangle are in proportion to the three sides of another triangle, then the two triangles are similar.

Thus, if AB/DE = BC/EF = AC/DF then ΔABC ~ΔDEF.

From this result, we can infer that ∠A = ∠D, ∠B = ∠E and ∠C = ∠F

Properties of Similar Triangle

1. Ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides
2.  Ratio of the areas of two similar triangles is equal to the ratio of the squares of corresponding altitudes and medians
3. In two similar triangles ABC and PQR

Examples:

1. Let ΔPQR, ΔDEF are similar triangles. If PQ = 6 and DE = 7, find A(ΔPQR)/A(ΔDEF)

Solution: A(ΔPQR)/A(ΔDEF) = PQ²/DE² = 36/49

2. If three sides of a triangle ABC and XYZ having coordinates A(-4, 0), B(0, 8), C(4, 0), X(-2,2), Y(0,6) and Z(2, 2). Prove that these triangles are similar.

Solution: Given Coordinates of the vertices

Calculate the ratios of the lengths of corresponding sides

From this we can tell that 

As, the lengths of the corresponding sides are proportional, we can say that triangles are similar.

  3. Find the length PQ in the triangle shown below

Solution:

∠PQR = ∠PST, ∠PRQ = ∠PTS and ∠P is the common angle => the two triangles ΔPQR and ΔPST are similar.

  2PQ = PQ + 6

  PQ = 6

  4. ABC and XYZ are two similar triangles with ZC = ZZ, whose areas are respectively 32 and 60.5 If XY = 7.7 cm, then what is AB equal to?

Solution: For similar triangles, ratio of areas is equal to the ratio of the squares of any two corresponding sides.

  5. ABC is a triangle right angled at A and a perpendicular AD is drawn on the hypotenuse BC. What is BCAD equal to?

Solution: In case of a right-angled triangle, if we draw a perpendicular from the vertex containing right angle to the hypotenuse,

we get three triangles, two smaller and one original and these three triangles are similar triangles.

So, ΔABC ~ ΔABD ~ ΔADC

Therefore, BC. AD = AB. AC

---

• Numbers play an important role in our day-to-day life.
• Puzzles based on these numbers are known as word problems.
•  To solve such problems, you have to extract the information correctly and form equations based on given information.
• The equations formed can be single variable, multi variables, linear, quadratic etc., depending on the type of problem asked.

Types of Word Problems Based on Numbers:

There are basically following types of questions that are asked on word problem on numbers.

 Type 1: Based on Operation with Numbers:

These types of questions include the operations like subtraction, addition, multiplication, division of number with other number, calculation of average of consecutive numbers, calculation of parts of a number, operation on even or odd numbers, calculation of sum or difference of reciprocal of numbers etc

• Consecutive natural numbers can be assumed as x - 2, x -1, x, x +1, x + 2......
• Consecutive even/odd natural numbers can be assumed x-3, x-1, x + 1, x + 3.......
• If sum of two numbers is given as S, then take one number as x and other as (S - x)
• If difference of two numbers is d, then take one number as x and other as (x + d) or (x - d)

Type 2: Based on Formation of Number with Digits:

These types of questions include formation of a number with digits and its difference with reciprocal of the same number, calculation of a number, if a number is added or subtracted to it. The digits get reversed etc.

• A two-digit number with x as unit digit and y as ten's digit is formed as (10y + x) and if the digits are reversed, then number is represented as (10x + y).
• A three-digit number with x as unit digit, y as ten's digit and z as hundred's digit is formed as (100z +10y + x).

Type 3: Question Regarding Calculation of Heads and Feet of Animals:

If a group of animals having either two feet (like ducks, hens etc) or four feet (like horses, cows etc) is there and total number of heads in the group are Hand number of feet of these animals are L, then Number of animals with four feet =

Number of animals with two feet = total number of heads – total number of four feeted animals

Examples:

1. A number is 25 more than its two-fifth. Find the number.

Solution. Let the number be y.

Then, according to the question,  

 2. The sum of the digits of a two-digit number is 10. The number formed by reversing the digits is 18 less than the original number. Find the original number.

Solution: Suppose the two-digit number = 10x + y and

 sum of the digits = x + y = 10…(i)

After reversing the digits, the new number = 10y + x

According to the question, (10x + y) - (10y + x) = 18

9x - 9y = 18

 x - y = 2 ...(ii)

On adding Eqs. (i) and (ii), we get

x + y = 10

x - y = 2

2x = 12

x = 6

On placing the value of x in Eq(i), we get y = 4

Therefore, original number = 10x + y = 10 x 6 + 4 = 64

 3. In a park, there are some cows and some ducks. If total number of heads in the park are 68 and number of their legs together is 198, then find the number of ducks in the park.

Solution: Given L = 198 and H = 68

• Therefore, number of ducks = number of heads – number of cows = 68 – 31 = 37

 4. The sum of five consecutive odd numbers is equal to 175. What is the sum of the second largest number and the square of the smallest number amongst them together?

Solution: Sum of five consecutive odd numbers

Sum of the second largest and square of smallest one = (31 + 6) + (31)² = 37 + 961 = 998

 5. A chocolate has 12 equal pieces. Peter gave 1/4th of it to Jack, 1/3rd of it to John and 1/6th of it to Fiza. The number of pieces of chocolate left with Peter is

Solution: The number of pieces of chocolate left with Peter = 

Hence, number of pieces of chocolate left with Peter is 3

---

A complex arithmetical expression can be converted into a simple expression by simplification. VBODMAS' Rule

To simplify arithmetic expressions, which involve various operations like brackets, multiplication, addition, etc; a particular sequence of the operations has to be followed.

The operations have to be carried out in the order, in which they appear in the word VBODMAS, where different letters of the word stand for following operations.

Order of removing brackets

First Small brackets (Circular brackets) ‘()'

 Second Middle brackets (Curly brackets) ’{}'

Third Square brackets (Big brackets) '[]'

V = Vinculum or Bar

B = Bracket

O = Of

D = Division

M = Multiplication

A = Addition

S = Subtraction

Order of above-mentioned operations is same as the order of letters in the 'VBODMAS' from left to right as

The order will be as follows:

First -> Vinculum bracket is solved

Second -> Brackets are to be solved in order given above, [first, then second, the third]

Third -> Operation of ‘Of’ is done,

Fourth -> Operation of division is performed,

Fifth -> Operation of multiplication is performed,

Sixth -> Operation of addition is performed,

Seventh -> Operation of subtraction is performed.

Note:

Absolute value of a real number

If m is a real number, then its absolute value is defined as

Example: |3| = 3 and |-3| = -(-3) = 3

Basic Formulae:

1. (a+ b) (a -b) = (a²-b²)
2. (a + b)² = a²+ b²+ 2ab
3. (a - b)² = a²+ b²- 2ab
4. (a + b+ c)² = a²+ b²+ c²+ 2ab + 2bc +2ca
5. (a + b)³ = a³ + b³ + 3ab (a + b)
6. (a - b)³ = a³ - b³ - 3ab (a - b)
7. (a³ + b³) = (a + b) (a²- ab+ b²)
8. (a³ - b³) = (a - b) (a² + ab+ b²)
9. a³ + b³ + c³ - 3abc = (a + b+ c) (a²+ b²+ c²- ab – bc - ca)
10. when a + b +c = 0, then a³ + b³ + c³ = 3abc
11. (a + b)²-(a - b)² = 4ab
12. (a + b)² + (a - b)² = 2(a²+ b²)

Examples:

1. Find the value of a³ + b³ + c³ -3abc, when a = 225, b = 226, c = 227

Solution: We know that,

a³ + b³ + c³ - 3abc = (a + b + c)  [(a - b)² + (b – c)² + (c – a)²]

                                               = (225 + 226 + 227)  [ 1 + 1 + 4]

                                              = 678 x 3

                                             = 2034

 2. Simplify 

Solution: Given expression 

                                                = 6 – [9 – {18 – (15 – 12 + 9)}]

                                                = 6 – [9 – {18 – 12}]

                                                = 6 – [9 – 6]

                                                = 6 – 3

                                                = 3

Solution: Given expression 

On dividing numerator and denominator by x,

we get

 4. A man divides $8600 among 5 sons, 4 daughters and 2 nephews. If each daughter receives four times as much as each nephew and each son receives five times as much as each nephew, how much does each daughter receive?

Solution: Let the share of each nephew be $ p.

Then, share of each daughter = $ 4p

Share of each son = $ 5p

So, 5 x 5p + 4 x 4p + 2 x p = 8600

  25p + 16p + 2p = 8600

  43p = 8600

  p = 200

So, share of each daughter = $ (4 x 200) = $ 800

 5. In a regular week, there are 5 working days and for each day, the working hours are 8. A man gets $ 2.40 per hour for regular work and $ 3.20 per hours for overtime. If he earns $ 432 in 4 weeks, then how many hours does he work for?

Solution: Suppose the man works overtime for t hours.

Now, working hours in 4 weeks = 5 x 8 x 4 = 160

 160 x 2.40 + t x 3.20 = 432

  3.20t = 432 – 384

  t = 15

Therefore, total hours of work = (160 + 15) = 175.

 

---

Co-prime numbers are the numbers having common factor as only 1. A pair of numbers whose highest common factor is 1 are said to be co-prime.

Let p and q are two positive integers, if they have 1 as their only common factor and thus HCF (x, y) = 1 they are called as Co-prime numbers.

• Co-prime numbers need not be prime numbers always.
• For example, {4 and 7}, {21 and 22} are co-prime numbers.

Finding co-prime numbers:

Let us take an example of {5, 12}

5 is a prime number -> 5 x 1

12 is not a prime number-> 2 x 2 x 3 x 1

Here 5 and 12 have only 1 as highest common factor

So, they are co-prime numbers

Important Points to remember:

• 1 is co-prime with every number
• Two prime numbers are always co-prime to each other because prime number has only 2 factors (number itself and 1)
• Any two successive numbers are always co-prime
• The sum of any two co-prime numbers is always coprime with their product
• The numbers whose unit digit is 0 and 5 can never be co-prime to each other
• Two even numbers cannot be co-prime to each other because they have a common factor two

Examples:

1. Check if 5, 7 and 9 are co-prime numbers?

Solution: Here 5 and 7 are prime numbers -> 5 x 1 = 5 and 7 x 1 = 7

                                    9 can be written as 3 x 3 x 1 = 9

The common factor of all the three is 1

So, they are co-prime numbers

2. Show that 850 and 1000 are not co-prime numbers

Solution: here 850 -> 2 x 425

                               -> 2 x 5 x 85

                               -> 2 x 2 x 5 x 5 x 17

                        1000 -> 2 x 500

                                  -> 2 x 2 x 250

                                  -> 2 x 2 x 2 x 5 x 5 x 5

Here we have common factors as 2 and 5

So, they are not co-prime numbers

3. Write any one co-prime number of 123 other than 122 and 124

Solution: here 123 -> 3 x 41 x 1

Given any one co-prime number of 123

So, 125 -> 5 x 5 x 5 x 1

Here 123 and 125 does not highest common factor other than 1.

So, 123 and 125 are co-prime numbers

4. 143 and 146 are co-prime numbers. True or False?

Solution:

143 -> 11 x 13 x 1

146 -> 2 x 73 x 1

No, highest common factor other than 1

True, they are co-prime numbers

5. 11, 12 are co-prime numbers, check if sum of the co-prime numbers is co-prime with the product of the co-prime numbers.

Solution: sum = 11 + 12 = 23, product = 11 x 12 = 132

Here sum 23 is a prime number -> 23 x 1

Product 132 -> 2 x 2 x 3 x 11 x 1

23 and 132 does not have any common factor other than 1.

So, sum of the co-prime numbers is co-prime with the product of the co-prime numbers

 

---

Statistics is a branch of mathematics that deals with numbers and analysis of the data. Statistics is the study of the collection, analysis, interpretation, presentation, and organization of data.

In short, Statistics deals with collecting, classifying, arranging, and presenting collected numerical data in simple comprehensible ways.

With the help of statistics, we are able to find various measures of central tendencies and the deviation of data values from the center.

Basic Formulae:

• Mean is defined as the sum of all the elements of a set divided by the number of elements.

• Median is the middle value of a dataset.
• If a set consists of an odd number of values, then the middle value will be the median of the set.
•  If the set consists of an even number of sets, then the median will be the average of the two middle values.

Median(M) = If n is odd, then 

If n is even, then 

• The mode in a dataset is the value that is most frequent in the dataset.

Mode = The value which occurs most frequently

• 
• The standard deviation is defined as the square rooting of the variance of the data.

Standard Deviation(S) = 

Where, x = observations given

 = Mean

 = Total number of observations

 

1. In a group of 10, 4 students were selected at random and their total marks in the final assessments are recorded, which are 81, 83, 98, 76. Find the standard deviation of their marks.

Solution: Here N = 4

 2. Weight of girls = {40, 45, 50, 45, 55, 45, 60, 45}. Find the mode?

Solution: Here we have 45 as repeating value

Since only on value is repeating it is a unimodal list.

S0, mode = 45

 3. Find the median of the data: 24, 36, 45, 18, 20, 26, 38

Solution: Arrange them in ascending order 18, 20, 24, 26, 36, 38, 45

Median = middle most observation or  term when n is odd

So, median = 26

 4. All the students in a mathematics class took a 100-point test. Eight students scored 100, each student scored at least 55, and the mean score was 75.

What is the smallest possible number of students in the class?

Solution:

• Let the number of students be 
• Then the sum of their scores is at least 
• we need to achieve the mean 75, which is equivalent to achieving the sum 75n.

• we must have 
• The smallest integer n for which this is true is n = 18.
• To finish our solution, we now need to find one way how 18 students could have scored on the test.
• We have 18 x 75 = 1350 points to divide among them.
• The eight 100s make 800, hence we must divide the remaining 550 points among the other 10 students.
• This can be done by giving 55 points to each of them.
• Hence the smallest possible number of students is 18.

 5. A manager has given a test to his team in which 20% are women and 80% are men. The average score on the test was 70. Women all received the same score, and the average score of the men was 60. What score did each of the woman receive on the test?

• Solution:

  • Let Total students = 100, Men = 80, Women = 20.
  • Sum of all the scores = 100 x 70 = 7000.
  • Sum of all the scores of men = 60 * 90 = 5400.
  • Difference in scores = 7000 - 5400= 1600.
  • 1600 is the scores obtained by women.
  • It's stated in the question that all Girls got the same score
  • so, score each of the woman received on the test 1600/20 = 80.

---

1. It is a COMINATION if the order of selection DOES NOT matter

Combinations have the formula of ⁿC_r

Where:

               n = number of things to be chosen from (the population)

               r = number in group/team/category

 The numerator is just the factorial n! taken “r” times, and the denominator is just the factorial r! taken “r” times

Ex: ⁵C₂   

  A larger factorial can be simplified down by simply subtracting (n-r) for r

      Ex: ¹⁹C₁₇ = ¹⁹C₂ where r = (19 - 17) = 2

 2. It is a PERMUTATION if the order of selection DOES matter

Permutations have the formula of ⁿP_r = ⁿC_r x r! 

  Permutations can be simplified to just the numerator portion of the combination 

EXAMPLE 1: If there are 4 tennis players and you need to make teams of 2 consisting of a captain and vice-captain, how many different teams can you make?

COMBINATION & PERMUTATION RULES EXPLAINED WITH EXAMPLES:

1. If you have 10 children, how many ways can they stand in a row? 

Ans-> 10!

2. You have 4 physics books, 3 math books, and 2 chemistry books. How many ways can they be arranged on a shelf?

Ans-> 9! -> There are 9 totally different books

3. You have the same set of books as above, but all physics books must stay together, all math books must stay together, and all chemistry books must stay together on the shelf. How many ways can they be arranged?

Ans-> 3! x 4! x 3! x 2!  = 1,728

Think of each set of books going into a “box” or a “set” on the shelf. This creates 3 different “sets” – one for physics, one for chemistry, and one for math. Then within each “box” or “set”, the different books can be arranged as many times as there are books.

So, there are 3 different book types, giving 3!

Then there are 4 physics books, 3 math, and 2 chem books, giving 4!, 3!, and 2! Respectively, totalling 3! x (4! x 3! x 2!) = 1,728

4. Same set of books as above, however all of the books are identical for each type (all physics books are the same, math is the same, chem are the same). How many ways can they be arranged on the shelf? 

Ans-> 3!  There is no differentiation between the books, except the type of book they are

5. How many ways can the word “at” be arranged? (Or any 2-character combination) 

Ans-> 2!

6. How many ways can the word “top” be arranged? (Or any 3-character combination) 

Ans -> 3! 

7. How many ways can the word “too” be arranged? (Or any 3-character word with 2 identical characters)

Any X character combination with Y identical characters has  number of arrangements where X is the total number of characters and Y is the number of identical characters. If there are more than 1 set of identical characters, put them all in the denominator.

 8. How many ways can the word “mathematics” be arranged?

  because there are 2 instances of “m”, “a” and “t” each

 9. A person is standing downtown at point A and wishes to get to the other side of downtown to point B. There are 5 streets and 4 crossroads. How many ways can he get from A to B?

There are 9 total streets, and no matter what, he must go 4 ways right and 5 ways up.

 10. There are 6 people sitting at a circular table. How many ways can they be seated? 

Ans -> (6 -1)!

For a “circular problem” you have to subtract 1 from the possibilities – any arrangement will always start and end with the same person.

 11. A father has the following bills in his pocket - $5, $10, and $20. His son asks for some spending money for the weekend. How many ways can the father give his son some money? 

Ans -> 2³

For each bill, the father has the option to either give it to his son or not. Then the father could also give a combination of any of the bills or not 

 12. The same scenario exists, but the father must give his son at least something to spend

Ans -> 2³ – 1   you have to subtract the scenario of giving him neither of any of the bills

 13. At Walmart there is a box of 100 different $0.99 items in it at the register. How many ways can a shopper grab some of the items?

Ans: 2¹⁰⁰            she has the option to grab or not grab each item

         2¹⁰⁰ – 1     if she must choose at least 1 item

 15. A teacher has a pen, an eraser, and tape. She wants to distribute these among 2 students. How many ways can she distribute these items where all 3 must be distributed among the 2 students? 

Ans -> 2³ = 8

Rⁿ is the general equation used for these question types, where n is the number of objects to be distributed and R is the number of people (or groups) among which the n objects are to be distributed.

If you want to include the option of not distributing anything, add 1  Rⁿ +1

 15. There are now 3 students in the class and the teacher has a pen, eraser, tape, and stapler. How many ways can she distribute the items if all must be distributed? If none can be distributed?

Ans -> 3⁴; 3⁴ + 1

 16. A teacher has 5 identical chocolates and wants to give them to her 3 students. How many ways can she give the chocolates to the students?

Ans-> ^(5+3-1) C_{3 – 1} = ⁷C2 

For N identical items being distributed among R people (or groups) the following formula should be used: ^N+(R-1) C _(R-1) 

If all items must be distributed, then the use the following formula: ^(N-1) C _(R-1)

 17. A teacher has 5 identical chocolates to give to 3 students and she must give each student something. How many ways can she distribute the chocolates?

(5 – 1)C_{3 – 1} = 4C₂

 18. How many ways can you pick fruit from a “For Sale” basket at the grocery store that has 5 oranges, 6 apples, and 7 bananas in it?

(5 + 1) (6 + 1) (7 + 1) = 6 x 7 x 8 = 336

The “ + 1” is to account for the option of not picking that particular item

 19. If you must pick at least one fruit from the basket, how many ways can you pick fruit?

(5 + 1)(6 + 1)(7 + 1) – 1 = (6 x 7 x 8) – 1 = 336 – 1 = 335

 20. How many ways can you pick fruit from a basket with 10 apples, 15 oranges, and 25 other different types of fruit?

(10 + 1)(15 + 1)(2²⁵) = (11)(16)(2²⁵) = (11)(2²⁹)

The oranges and apples are identical; the 25 other types are all different, and for each one you can either chose one or not

 21. A man, his wife, and their child go to a movie theatre with 5 seats and all three must sit together. How many ways can they sit at the theatre?

[5 – (3+1)] x 3!

3! is for the different combinations the father, mother, and child can sit together (similar to the “boxes” or “sets” of the similar textbooks)

[n – (r+1)] gives you the number of seating arrangements where n is the number of seats and r is number of people

 22. A man, wife, daughter, and son go to a movie theatre with 10 seats and they all want to sit together. How many ways can they sit?

(10 – 4 + 1) x 4! = 7 x 4!

 23. In how many ways can 8 tennis players be divided into 2 distinct teams of 4 each?

(4 x 2)! / 4!²

Use the formula (m x n)! / n!^m

Or (m x n)! / (n!^m x m!) for non-distinct teams

 24. How many ways can 8 tennis players be divided into 2 non distinct teams of 4 each?

(4 x 2)! / (4!² x 2!) 

 25. You have 10 pants, 20 shirts, and 5 shoes in your closet. You’re packing for a trip and want to take two of each. How many ways can you pack a suitcase? 

10C₂ x 15C₂ x 5C₂ = 5 x 9 x 10 x 19 x 5 x 2

 26. There are 6 total horses in a race, two of which are ridden by Bob and John. How many ways can John be ahead of Bob?

 27.  How many ways can you rearrange the word “courage” with the vowels staying in alphabetical order?

7! Represents the total number of letters in “courage” and 4! Represents the vowels that must stay in order 

 28. You want to create a 5-character password, and the first character must be a consonant, the second must be a vowel, and the rest can be digits. How many 5 passwords can be created? 

21 x 5 x 10 x 10 x 10      21 consonants, 5 vowels, and 10 different digits

 29. There are 5 men and 3 women in a department.  They need to form a 3-member committee with at least one woman in the committee?

 30. 

3 member committee out of 8 staff = 8c3 = (8 * 7 * 6)/(1 * 2 * 3) = 56

All men committees = 5c3 = (5 * 4)/1 * 2 = 10

Required Committees = Total possible committees - All men committees) = 56 – 10 = 46

 31.  A coin is tossed 5 times (or 5 coins are tossed one time).  What are the different outcomes?

First let us do it for 3 tosses. 

T T T

 

H T T

T H T

T T H

 

H H T

H T H

T H H

 

H H H

Total Sample Space = = 8

Outcomes = 2 ( Head or Tail)

Experiment = Number of tosses = 3 

If it is 5 tosses = = 32 is the total sample space

   

Total = 8/8 = 1

For five tosses:

If it is 5 tosses = = 32 is the total sample space

 32. There are 5 Black cars and 3 White cars in a car dealership.  How many ways one can pick two cars in the following cases:

Black             White                   Pick

5                    3                            2

B                    B                            5c2/8c2 = 10/28

W                   W                         3c2/8c2 = 3/28

B                    W                          5c1 * 3c1/8c2 = 5 * 3/{(8 * 7)/(1 * 2)} = 15/28

 

32.

There are 5 Black cars, 4 Red cars and 3 White cars. 

Pick any two cars:

1. Both Black 5c2/12c2
2. Both Red  4c2/12c2
3. Both White 3c2/12c2
4. Different Color BR + BW + RW {(5c1 * 4c1) + (5c1 * 3c1) + (4c1 * 3c1)}/12c2
5. Same Color (5c2 + 4c2 + 3c2)/12c2
6. Any two Colors BR + BW + RW {(5c1 * 4c1) + (5c1 * 3c1) + (4c1 * 3c1)}/12c2   

Pick any 3 cars

1. All three same color (5c3 + 4c3 + 3c3)/12c3
2. All three different color  (5c1 * 4c1 * 3c1)/12c3

33.

7 married couples-Mixed double teams without married couples

The number of ways a lawn tennis mixed double can be made up from seven married couple if no husband and wife play in same set is.

Answer: 36

Total = 14

7 husbands * 7 wives = 49 ways

Out of above 49, 7 are married to each other

Mixed double teams without married couple = 49 – 7 = 36

34.

Arrangements

There are 5 married couples and a group of three is to be formed out of them; how many arrangements are there if a husband and wife may not be in the same group?

Answer: 80

First member can be chosen from one of the couples in 5c1 ways

Four couples left. 

The remaining two members can be chosen in 2^4 ways from 4 couples = 5 * 2^4 = 80 ways

or

10c3 = 10.9.8/3.2 = 120

1 couple can be selected in 5c1 ways = 5

This can couple can be with any other 8 people in 8 ways

1 couple in 3 = 5 * 8 = 40

Answer = 120-40 = 80

---

Sample Space:

The set of all possible outcomes of an experiment is called the sample space, denoted by S. An element of S is called a sample point.

An Event:

Any subset of a sample space is an event.

Tossing a Coin

On tossing a coin certainty of occurrence of each of a head and a tail are the same.

Hence amount certainty of occurrence of each of a head and a tail is 50% i.e., 50/100 = 2

Therefore, is the amount of certainty of occurrence of a head (or a tail) on tossing a coin

So, we say that the probability of getting H is 1/2 or the probability of getting T is 1/2.

In the experiment of tossing a coin, the sample space has two points corresponding to head (H) and Tail (T) i.e., S {H, T}.

Here Let A be event of occurrence a head (or Tail) and S be the sample space

• P(A) 

Throwing a Die

On throwing a dice certainty of occurrence of each of the numbers 1, 2, 3, 4, 5 and 6 on its top face are the same

Dice: Dice is a cuboid having one of the numbers 1, 2, 3, 4, 5 and 6 on each of its six faces

When a single die is thrown, there are six possible outcomes 1, 2, 3, 4, 5 and 6.

The probability of getting any one of these numbers is 

When we throw a dice then any one of the numbers 1, 2, 3, 4, 5 and 6 will come up.

So, the sample space, S = {1, 2, 3, 4, 5, 6}

Here Let A be event of occurrence any number from 1 to 6 and S be the sample space.

• P(A) 

CONDITIONAL PROBABILITY:

Let A and B be two events associated with a random experiment.

Then, the probability of occurrence of A under the condition that B has already occurred and P (B) ≠ 0, is called the conditional probability of occurrence of A when B has already occurred and it is denoted by P (A/B).

Thus, P (A/B) = Probability of occurrence of A, if B has already occurred and P (B) ≠ 0

Similarly, P(B/A) = Probability of occurrence of B, if A has already occurred and P(B) ≠ 0

Examples:

1. Two dice are thrown simultaneously. The probability of obtaining a total score of seven is

Solution:

Two dice are thrown then we have 6 × 6 exhaustive cases

So, n = 36.

Let A be the event of “total score of 7”

When 2 dice are thrown then A = [(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)].

Total number of favourable cases = 6

Therefore, P(A) 

 2. The probability of getting head and tail alternately in three throws of a coin (or a throw of three coins), is

Solution:

Total probable ways = 8

Favourable number of ways = HTH, THT

 Required probability 

 3. Suppose six coins are tossed simultaneously. Then the probability of getting at least one head is:

Solution: Given six coins are tossed, then the total no. of outcomes = (2)⁶ = 64

Now, probability of getting no head 

Probability of getting at least one head 

 4. A dice is thrown twice. The probability of getting 4,5 or 6 in the first throw and 1, 2, 3 or 4 in the second throw is

Solution:

Let P (A) be the probability of the event of getting 4, 5 or 6 in the first throw

Let P (B) be the probability of the event of getting 1, 2, 3 or 4 in the second throw,

Then P (A and B) = P(A). P(B) 

 5. A coin is tossed and a dice is rolled. The probability that the coin shows the tail and the dice shows 5 is

Solution:

 Probability of getting a tail on tossing a coin (P₁) 

 Probability of getting a five on rolling a dice (P₂) 

These two events are independent.

Required Probability 

---

A Venn diagram is a diagram that helps us visualize the logical relationship between sets and their elements.

It shows logical relations between two or more sets

Venn diagrams are also called logic or set diagrams

They are widely used in set theory, logic, math, teaching, business data science and statistics.

 A Venn diagram typically uses circles other closed figures can also be used to denote the relationship between sets.

In general, Venn diagrams shows how the given items are similar and different

In Venn diagram 2 or 3 circles are most used one, there are many Venn diagrams with larger number of circles (5, 6, 7, 8, 10….).

Union: When two or more sets intersect, all different elements present in sets are collectively called as union.

It is represented by U

Union includes all the elements which are either present in Set A or set B or in both A and B

i.e., A ∪ B = {x: x ∈ A or x ∈ B}.

The union of set corresponds to logical OR

For example: If we have A = {1, 2, 3, 4, 5} and B = {3, 5, 7}

A U B = {1, 2, 3, 4, 5, 7}

Intersection: When two or more sets intersect, overlap in the middle of the Venn diagram is called intersection.

This intersection contains the common elements in all the sets that overlap.

It is denoted by ∩

All those elements that are present in both A and B sets denotes the intersection of A and B. So, we can write as A ∩ B = {x: x ∈ A and x ∈ B}.

The intersection of set corresponds to the logical AND

For example: If we have A = {1, 2, 3, 4, 5} and B = {4, 5, 6, 7}

A ∩ B = {4, 5}

Cardinal Number of Set:

The number of different elements in a finite set is called its cardinal number of a set

It is denoted as n(A)

A = {1, 2, 3, 4, 5, 7}

n(A) = 6

Formula:

• n (A ∪ B) = n(A) + n(B) – n (A ∩ B)
• n (A ∪ B ∪ C) = n(A) + n(B) + n(C) – n (A ∩ B) – n (B ∩ C) – n (C ∩ A) + n (A ∩ B ∩ C)

Examples:

1. Out of 20 boys, 5 boys have ice-cream only and 10 boys have chocolate only, 3 boys have both chocolate and ice-cream, how many boys has only one of ice-cream or chocolate.

Solution: Given total boys= 20

Number of boys having ice-cream = 5

number of boys having chocolate = 10

number of boys who has only one of ice-cream or chocolate = 5 + 10 = 15

2. In a class of 60 students, 21 play Tennis, 13 play Cricket and 14 play Basketball. 6 plays both Tennis and Cricket, 5 play Cricket and Basketball and 7 play Tennis and Basketball. If 22 students do not play any of these given sports, how many students play exactly two of these sports?

Solution: Given Total = 60;

 T = 21, C=13, and B=14; 

T ∩ C=6, C ∩ B = 5, and T ∩ B = 7.

Neither=19.

[Total] = Tennis + Cricket + Basket Ball – (TC+CB+TB) + (All three) + (Neither)

55 = 21 + 13 + 14 - (6+5+7) + (All three) + 22

(All three) = 3;

Students play only Tennis and Cricket are 6-3=3;

Students play only Cricket and Basketball are 5-3=2;

 Students play only Tennis and Basketball are 7-3 = 4;

 Hence, 3 + 2 + 4 = 9 students play exactly two of these sports.

 3. Last month 30 students of a certain college travelled to Egypt, 30 students travelled to India, and 36 students travelled to Italy. Last month no students of the college travelled to both Egypt and India, 10 students travelled to both Egypt and Italy, and 17 students travelled to both India and Italy. How many students of the college travelled to at least one of these three countries last month?

Solution: Given

Students travelled to Egypt n(A) = 30

Students travelled to India n(B) = 30

Students travelled to Italy n(C) = 36

Egypt and India travellers n (A∩ B) = 0

Egypt and Italy travellers n (A ∩ C) = 10

India and Italy travellers n (B ∩ C) = 17

From all the information we can determine that 0 people travelled to all 3 countries because 0 people travelled to both Egypt and India.

To know how many students travelled to at least one country,

Total travellers = Egypt + India + Italy - sum of (travelled exactly two countries) - 2 times (travelled all three countries)

Total travellers = 30 + 30 + 36 - (10 + 17 + 0) - 2(0)

Total travellers = 96 - 17 - 0 = 69

Thus, 69 people travelled to at least one country.

 4. Each person who attended a conference was either a client of the company, or an employee of the company or both. If 56 percent of these who attended the conference were clients and 49 percent were employees. What percent were clients, who were not employees?

Solution: Total = Stockholders + Employees - Both;

100 = 56 + 49 – Both

 Both = 5;

Percent of clients, who were not employees is: Clients - Both = 56 - 5 = 51.

 5. There are 45 students in PQR College. Of these, 20 have taken an accounting course, 20 have taken a course in finance and 12 have taken a marketing course. 7 of the students have taken exactly two of the courses and 1 student has taken all three of the courses. How many of the 40 students have taken none of the courses?

Solution:  Given Total= 45; Let P = 20, Q = 20, and R = 12; sum of EXACTLY 2 - group overlaps = 7;

P ∩ Q ∩ R =1;

Total = P + Q + R – (sum of exactly 2 – group overlaps) – 2 * P ∩ Q ∩ R + None

45 = 20 + 20 + 12 – 7 – (2 * 1) + none

None = 2

---