1 Problem Based on Ages
N/A
Age is defined as a period of time that a person has lived or a thing has existed. Age is measured in months, years, decades and so on.
Problem based on ages generally consists of information of ages of two or more persons and a relation between their ages in present/future/past.
Using the information, it is asked to calculate the ages of one 01 more persons in present/future/ past.
Important Rules for Problem Based on Ages:
Rule1:

Rule2:
If ratio of present ages of A and B is x: y and after n yr, the ratio of their ages will be p: q,

Note:
Mostly questions on ages can be solved with the use of linear equations.
Examples:
- Present age of Kevin is 5 times the age of Steve. After 10 yr, Kevin will be 3 times as old as Steve. What are the present ages of Kevin and Steve?
Solution: Let the present age of Steve be x yr. Then, present age of Kevin = 5x yr
After 10 yr, the ratio of ages will be 3: 1.
According to the question,
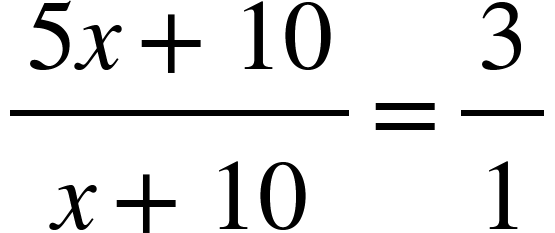
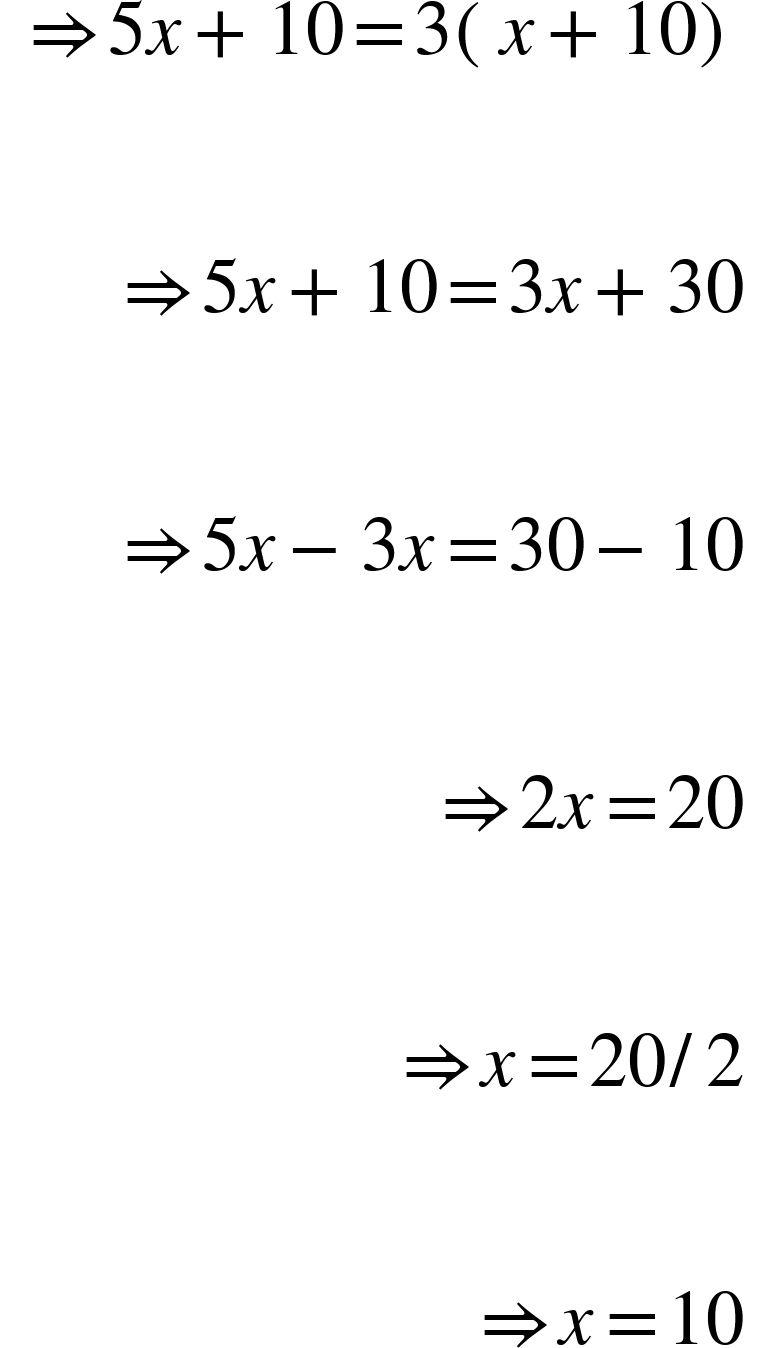
Therefore, Kevin’s present age = 5 x 10 = 50 yr and Steve’s present age = 10 yr
- The average age of a family of five members is 24. If the present age of the youngest member is 8 yr, what was the average age of the family at the time of the birth of the youngest member?
Solution: Total age of five members of a family = 24 x 5 = 120
Therefore, total age of four members at the time of birth of youngest = 120 – (8 x 5)
= 120 – 40 = 80 yr

- Before 7 yr, the ratio of ages of A and B was 3: After 9 yr, ratio of their ages will be 7: 8. The present age of B will be
Solution: Let the ages of A and B before 7 yr were 3x yr and 4x yr, respectively.
Therefore, present age of A = 3x + 7 and present age of B = 4x + 7

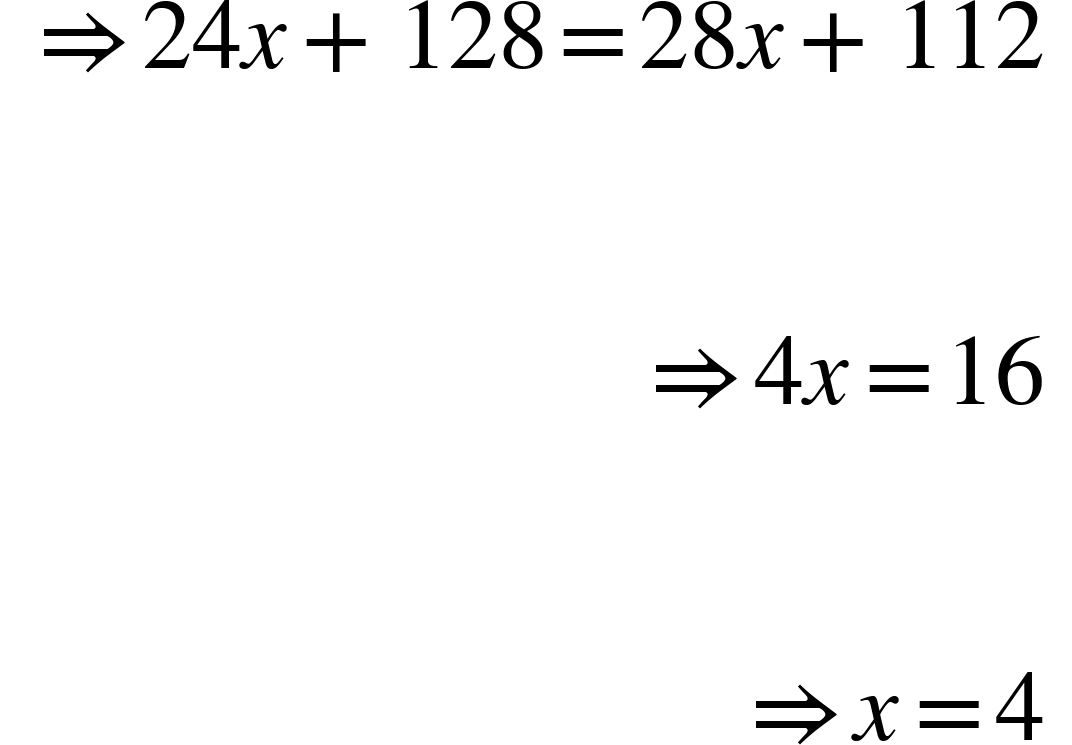
Hence, present age of B = 4 x 4 + 7 = 16 + 7 = 23 yr
4. The present ages of two persons are 36 and 50 yr, respectively. If after n yr the ratio of their ages will be 3: 4, then the value of n is
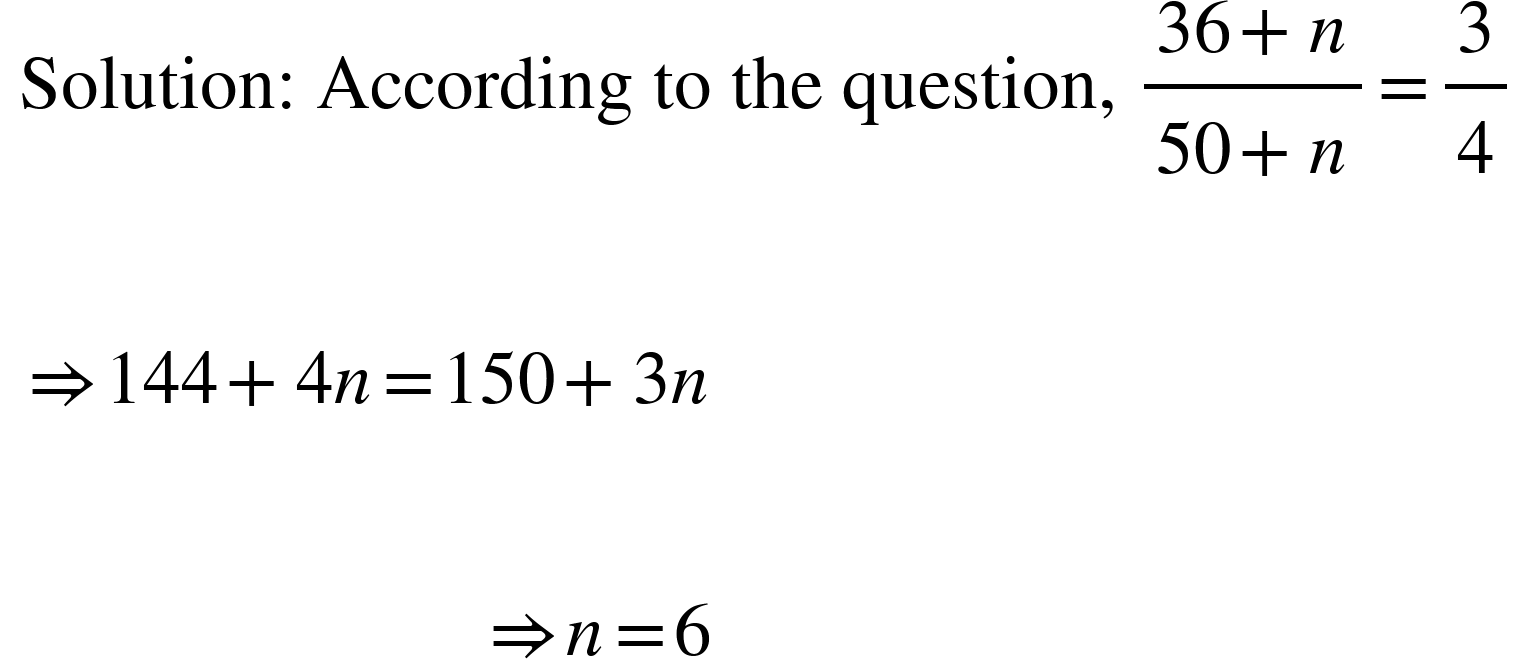
5. The present age of Peter's father is four times Peter's present age. Five years back, Peter's father was seven times as old as Peter was at that time. What is the present age of Peter's father?
Solution: Let present age of Peter be x.
Then, present age of Peter’s father = 4x
Now, 5 yr ago, Peter's father's age = 7x
Peter's age => 4x - 5 = 7(x - 5)
=> 4x - 5 = 7x - 35
=> 3x = 30
=> x = 10
Peter's present age = x = 10 yr
Peter's father's present age 4x = 4 * 10 = 40 yr
Unitary method is a fundamental tool to solve arithmetic problems based on variation in quantities.
The method endorses a simple technique to find the amount related to unit quantity.
This method can be applied in questions based on time and work, speed and distance, work and wages etc.
Direct proportion:
Two quantities are said to be in direct proportion to each other, if on increasing (decreasing) a quantity, the other quantity also increases (decreases) to the same extent
i.e., (Quantity 1) ∞ (Quantity 2)
For example: Number of men ∞ Volume of work done (time constant)
i.e., if number of men increases, then the volume of work done also increases.
Similarly, if volume of work increases, then number of men required to finish the work also increases.
Indirect Proportion:
Two quantities are said to be in indirect proportion to each other, if on increasing (or decreasing) a quantity, the other quantity decreases (or increases) to the same extent

For example:
The time taken by a vehicle in covering a certain distance is inversely proportional to the speed of the vehicle.
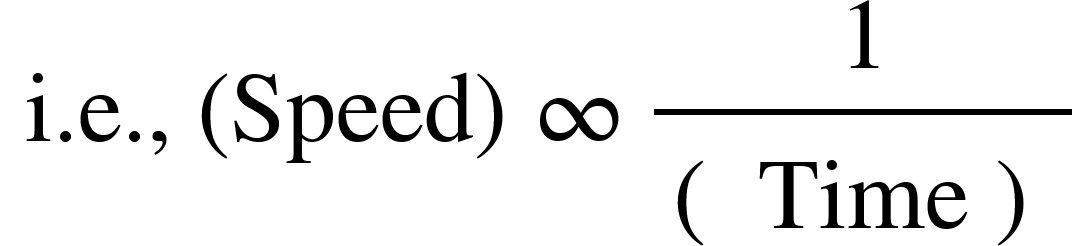
Note: If M1 persons can do W1 work in D1 days and M2 persons can do W2 work in D2 days, then we have a general formula, M1 W2 D1 = M2 W1 D2
- If 30 men working 18 h per day can reap a field in 32 days, in how many days can 36 men reap the field working 16 h per day?
Solution: Let the required number of days be ‘d’.
More men, less days (Indirect proportion)
Less hours, more days (Indirect proportion)


Therefore, Required number of days = 30
- Steve completes 5/8 of a job in 20 days. At this rate, how many more days will he take to finish the job?
Solution: Let the required number of days be ‘d’.
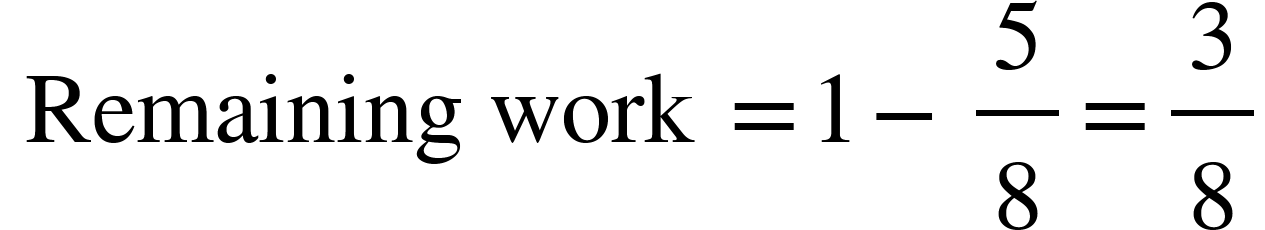
Less work, Less days (Direct proportion)
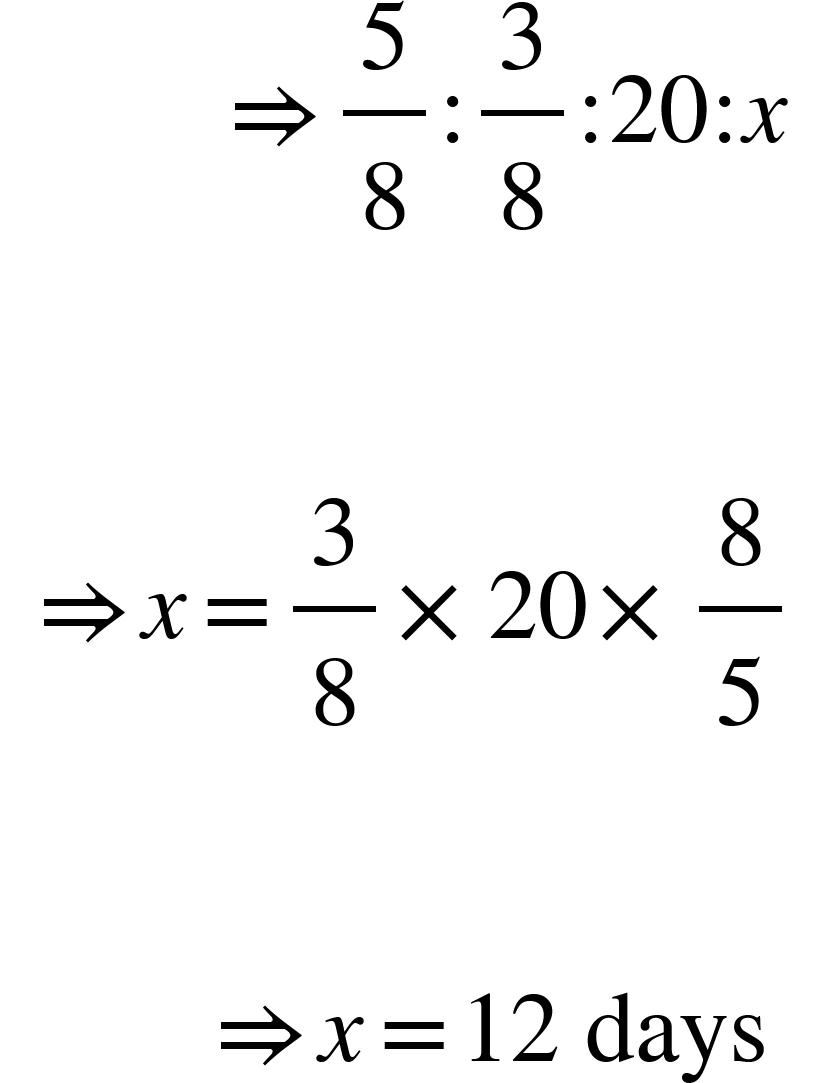
- If in a hostel, food is available for 45 days for 50 students. For how many days will this food be sufficient for 75 students?
Solution: For 50, food is sufficient for 45 days.
Therefore, for 1 student food is sufficient for 45 x 50 days

4. If 12 engines consume 30 metric tonnes of coal when each is running 18 h per day, how much coal will be required for 16 engines, each running 24 h per day, it being given that 6 engines of former type consume as much as 8 engines of latter type?
Solution:
Let the required quantity of coal consumed be x.
More engines, More coal consumption (Direct proportion)
More hours, More coal consumption (Direct proportion)
Less rate of consumption, Less coal consumption (Direct proportion)
Engines 12: 16
Working hours 18: 24

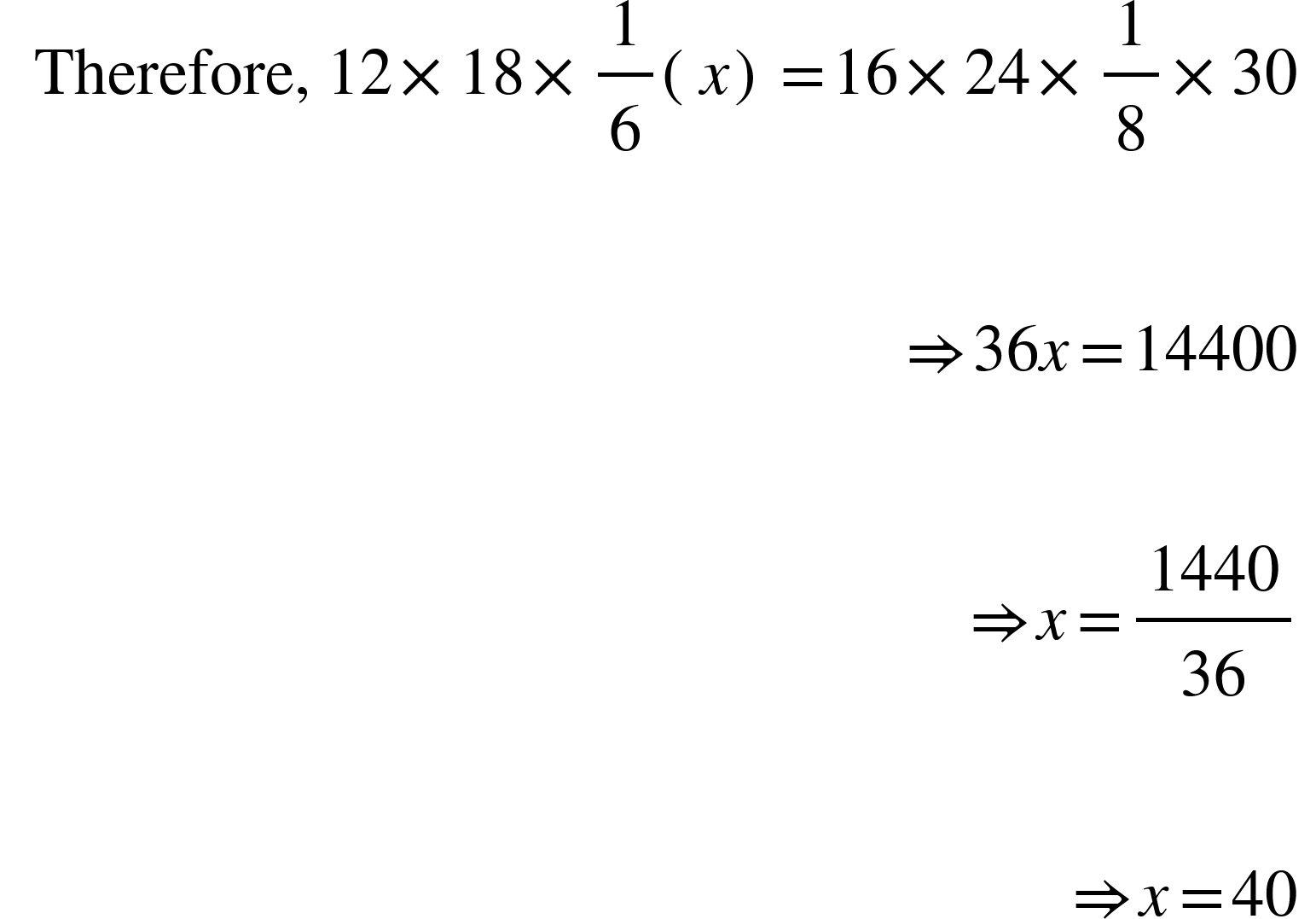
- A worker makes a toy in every 2 h. If he works for 80 h, then how many toys will he make?
Solution: Let number of toys be x.
More hours, more toys (Direct proportion)
2: 80:: 1: x
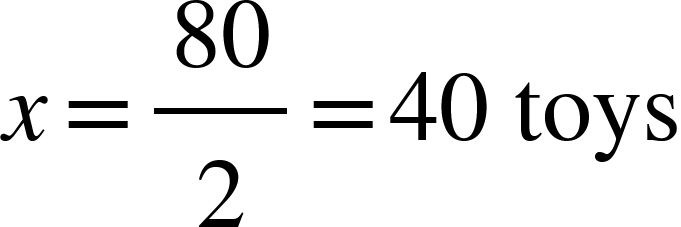
In this, we will study techniques to solve problems based on work and its completion time as well as number of persons required to finish the given work in stipulated time.
Suppose that you are a contractor and you got a contract to construct a flyover in a certain time. For this, you need to calculate the number of men required to finish the work according to their work efficiency.
Important Relations:
1. Work and Person Directly proportional (more work, more men and conversely more men, more work).
2. Time and Person Inversely proportional (more men, less time and conversely more time, less men).
3. Work and Time Directly proportional (more work, more time and conversely more time, more work).
Basic Rules Related to Work and Time:
Rule1: If a person can do a piece of work in n days, then that person’s 1 day’s (hour’s) work = (1/n)
Rule2: If a person’s 1 day’s(hour’s) work = (1/n), then the person will complete the work in n days(hours).
Rule3: If a person is n times efficient than the second person, then work done by
First person: Second person = n: 1 and time taken to complete a work by
First person: Second person = 1: n
Rule4: If ratio of numbers of men required to complete a work is m: n, then the ratio of time taken by them will be n: m
Examples:
- A and B together can do a piece of work in 12 days, while B alone can finish it in 30 days. A alone can finish the work in
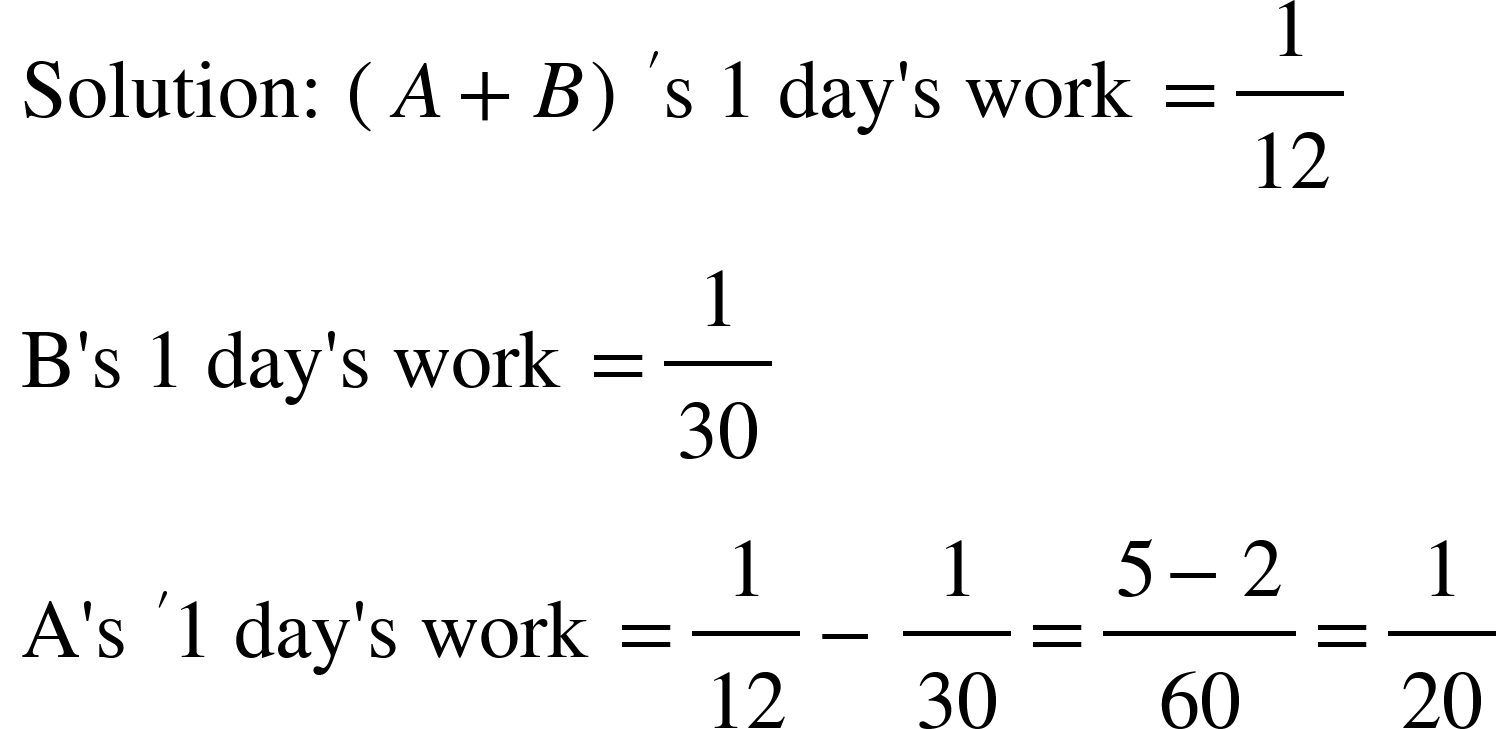
2. A can do a piece of work in 10 days and B in 20 days. They begin together but A leaves 2 days before the completion of the work. The whole work will be done in
Solution: Let the required days be x.
A works for (x-2) days, while B works for x days.
According to the question,
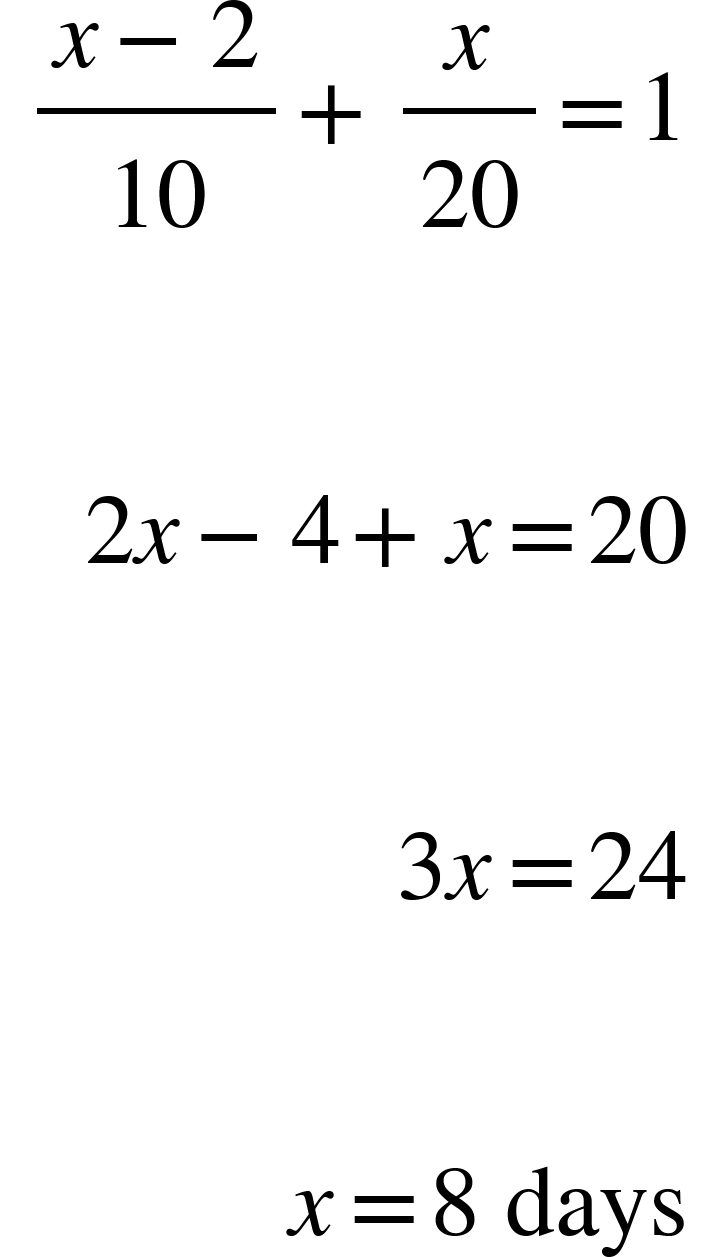
3. 6 boys can complete a piece of work in 16 h. In how many hours will 8 boys complete the same work?
Solution: Given, M1 = 120, D1 = 45, M2 = 120 + 30 = 150 and D2 = x
Then, using M1 D1 = M2 D2
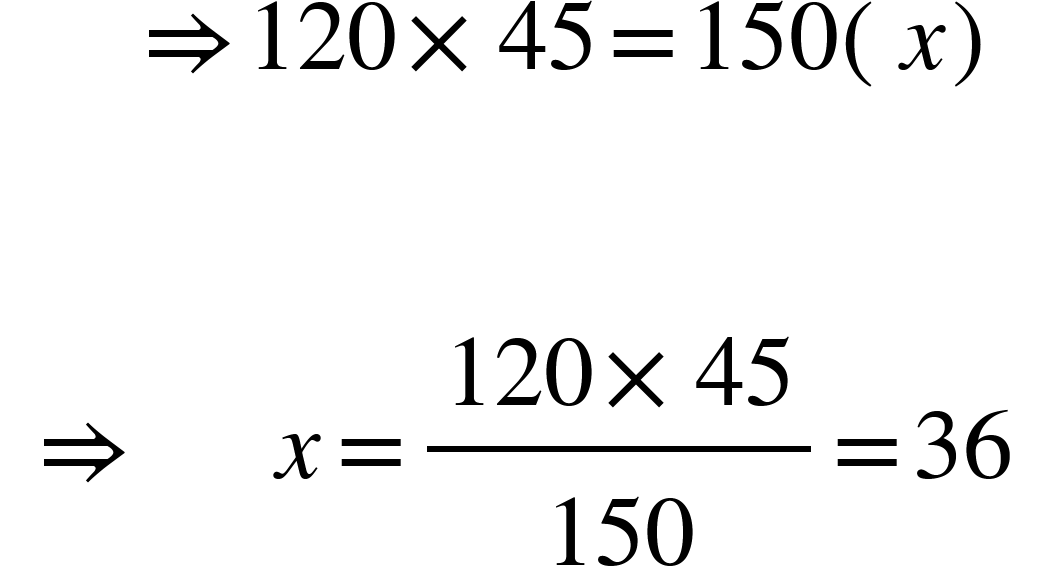
4. If 3 men or 4 women can build a wall in 43 days, in how many days can 7 men and 5 women build this wall?
Solution: 3 men = 4 women
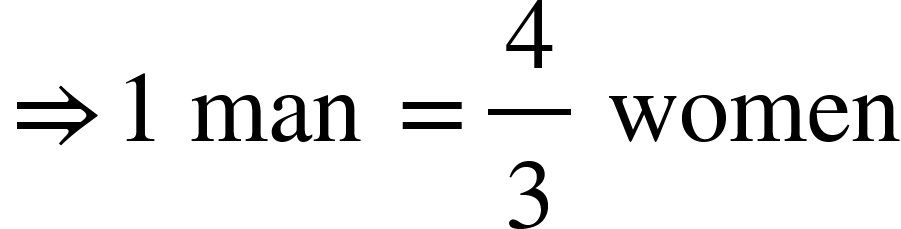

According to the formula, M1 D1 W2 = M2 D2 W1

Therefore, D2 = 3 x 4 = 12 days
5. A, B and C can do a piece of work individually in 8, 12 and 15 days, respectively. A and B start working but A quits after working for 2 days. After this, C joins B till the completion of work. In how many days will the work be completed?
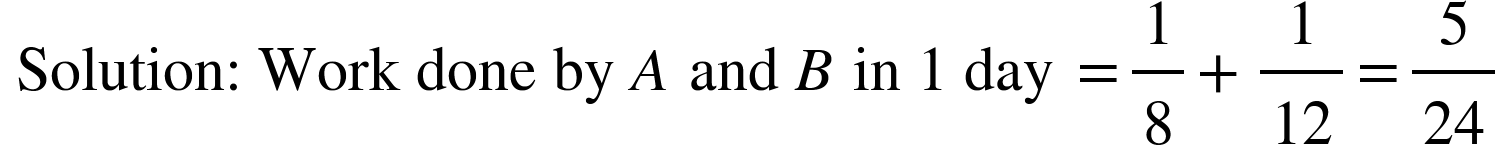
After 2 day’s A left the work
Activity involving physical efforts, done in order to achieve a result is known as work.
Money received by a person for a certain work is called the wages of the person for that particular work,
In other words, we can find the entire wages of any person by the following formula
Entire wages = Total number of days x Wages of 1 day of any person
For example:
If Arjun's monthly wages$ 4200 and he worked for all 30 days, then his daily wages will be calculated as Total wages = Number of days x Daily wages 4200 = 30 x Daily wages
Important Points:
- Wages is directly proportional to the work done. It means, more money will be received for more work and less money will be received for less work.
- Wages is indirectly proportional to the time taken by the individual.
- Wages is directly proportional to 1 day work of each individual.
Examples:
- Alex can do a piece of work in 6 days, while Kevin can do the same work in 5 days. If the total amount to be given for this work is $ 660, then what will be the share of Kevin, if both work together
Solution: Time taken by Alex = 6 days
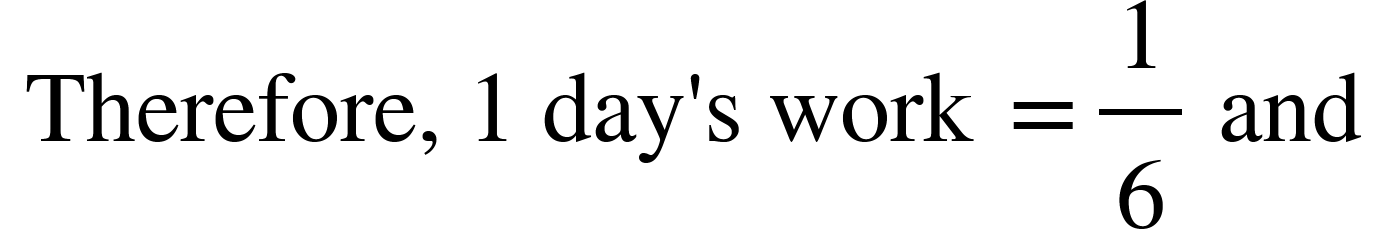
time taken by Kevin = 5 days

Total amount earned = $660
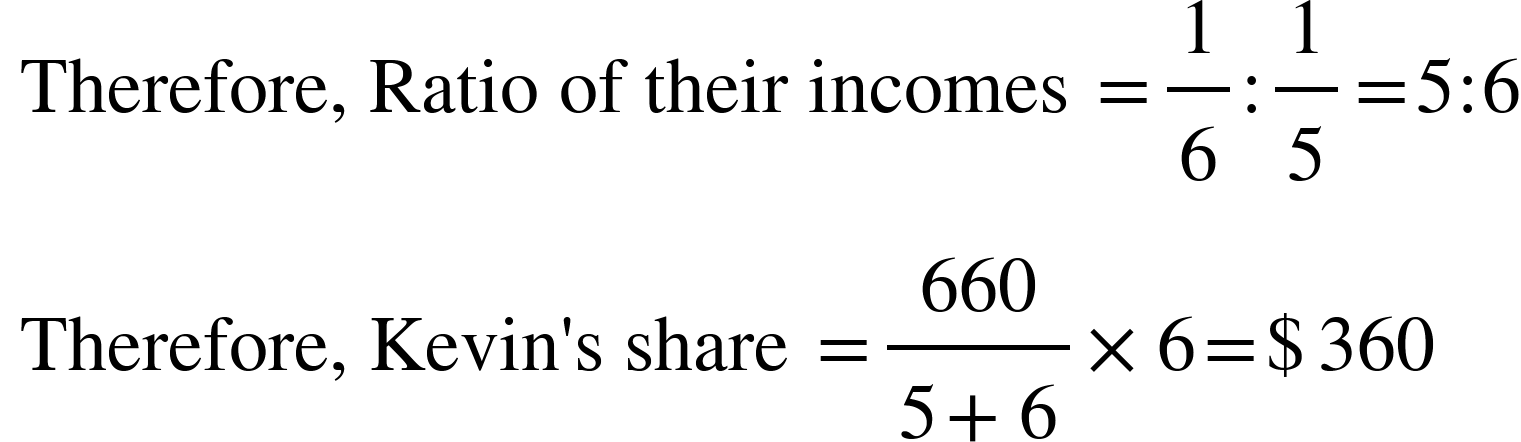
2. Wages of 45 women for 48 days amount to $ 31050. How many men must work for 16 days to receive $ 11500, if the daily wages of a man being double those of a woman?

3. Men, women and children are employed to do a work in the proportion of 3: 2: 1 and their wages as 5:3:2. When 90 men are employed, total daily wages of all amounts to $ 10350. Find the daily wages of a man.
Solution:
Let the numbers of men, women and children are 3y, 2y and y, respectively.
Given, 3y = 90 => y = 30
Number of women = 60 and number of children = 30
Let the men's, women's and children's wages be $ 5x, $ 3x and $ 2x, respectively.
According to the question,
Total daily wages = $ 10350
=> 90 x (5x) + 60 x (3x) + 30 x (2x) = 10350
=> x (450 + 180 + 60) = 10350
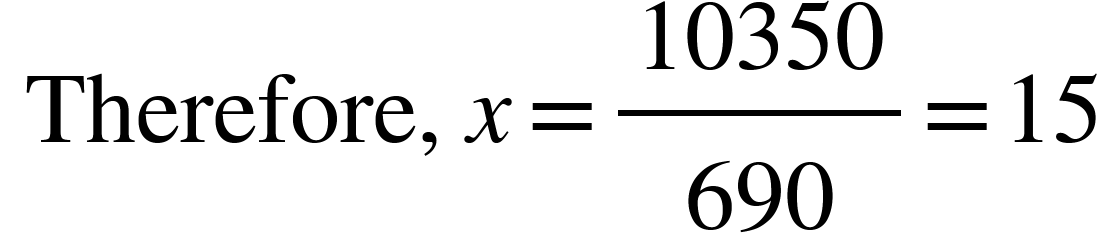
Therefore, Daily wages of a man = 15 x 5 = $ 75
4. A alone can finish a work in 2 days, while B alone can finish it in 3 days. If they work together to finish it, then out of total wages of $ 6000, what will be the 20% of A's share?

5. A man and a boy received $ 1400 as wages for 10 days for the work they did together. The man's efficiency in the work was six times that of the boy. What is the daily wages of the boy?
Solution: The ratio of efficiency of man to boy = 6: 1
Efficiency ∞ Wages
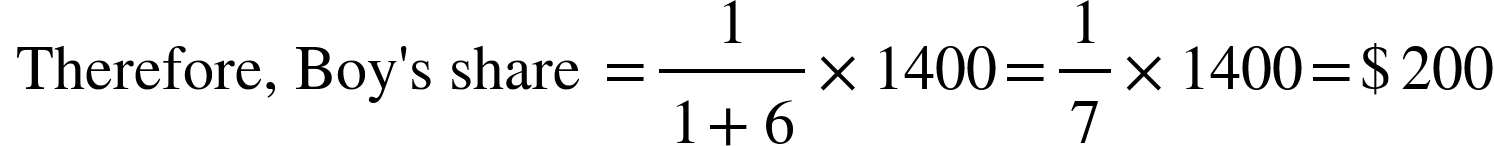
Now, they worked for 10 days.

Problems on Pipes and Cisterns are based on the basic concept of time and work
Pipes are connected to a tank or cistern and are used to fill or empty the tank or cistern.
In pipe and cistern, the work is done in form of filling or emptying a cistern/tank
Inlet pipe It fills a tank/cistern/reservoir. Outlet pipe It empties a tank/cistern/reservoir
Important Points:
- If a pipe can fill/empty a tank in m h, then the pat of tank filled/emptied in 1 hr =
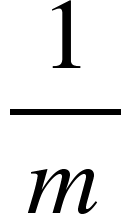
- If a pipe can fill/empty
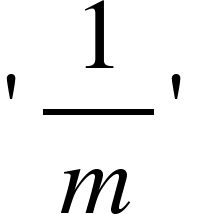 part of a tank in 1 h, then it can fill/empty the whole tank in ‘m’ h
part of a tank in 1 h, then it can fill/empty the whole tank in ‘m’ h
- Generally, time taken to fill a tank is taken(+ve) and time taken to empty a tank is taken negative(-ve).
- If a pipe fills a tank in m h and another pipe fills in n h. Then, part filled by both pipes in
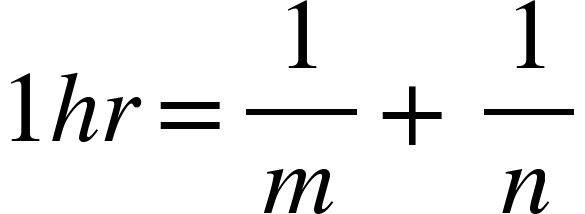
Examples:
- If a pipe can fill a tank in 2 h and another pipe can fill the same tank in 6 h, then what part of a tank will be filled by both the pipes in 1 h, if they are opened simultaneously?
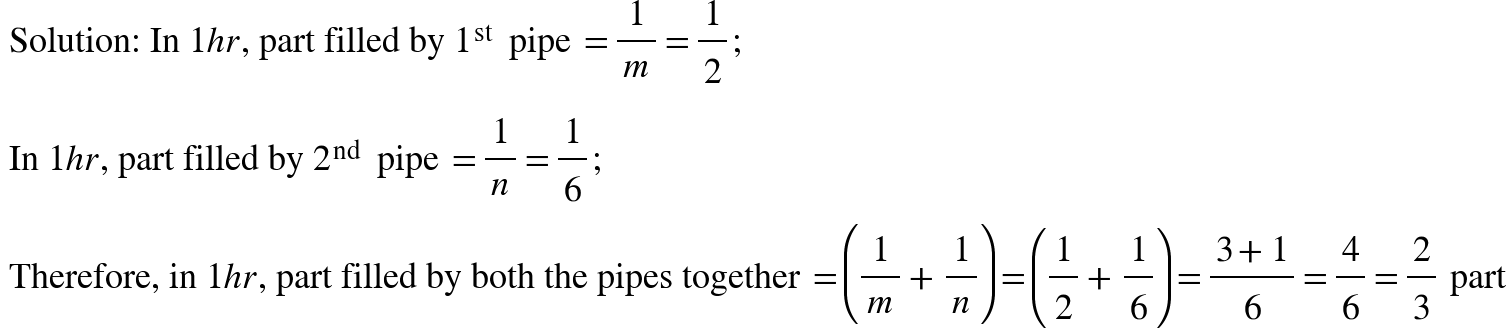
- A pipe can fill a tank in 10 h. Due to a leak in the bottom, it fills the tank in 20 h. If the tank is full, how much time will the leak take to empty it?
Solution: Let the leak empties full tank in x h, then part emptied in 1 h by leak = 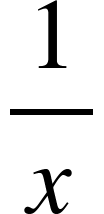
![text Also, part filled by u=inlet pipe in end text 1 h r equals 1 over 10
text According to the question, end text 1 over 10 plus 1 over x equals 1 over 20
text Therefore, end text 1 over x equals 1 over 20 minus 1 over 10 equals fraction numerator 1 minus 2 over denominator 20 end fraction equals negative 1 over 20 left square bracket text -ve sign means leak empties tank] end text <math xmlns="http://www.w3.org/1998/Math/MathML"><mtext> Also, part filled by u=inlet pipe in </mtext><mn>1</mn><mi>h</mi><mi>r</mi><mo>=</mo><mfrac><mn>1</mn><mn>10</mn></mfrac><mspace linebreak="newline"/><mtext> According to the question, </mtext><mfrac><mn>1</mn><mn>10</mn></mfrac><mo>+</mo><mfrac><mn>1</mn><mi>x</mi></mfrac><mo>=</mo><mfrac><mn>1</mn><mn>20</mn></mfrac><mspace linebreak="newline"/><mtext> Therefore, </mtext><mfrac><mn>1</mn><mi>x</mi></mfrac><mo>=</mo><mfrac><mn>1</mn><mn>20</mn></mfrac><mo>−</mo><mfrac><mn>1</mn><mn>10</mn></mfrac><mo>=</mo><mfrac><mrow><mn>1</mn><mo>−</mo><mn>2</mn></mrow><mn>20</mn></mfrac><mo>=</mo><mo>−</mo><mfrac><mn>1</mn><mn>20</mn></mfrac><mo>[</mo><mtext>-ve sign means leak empties tank]</mtext></math>](https://lh6.googleusercontent.com/vDL-5LQul_Fin1nrfJjMnn8WN19cJpnv0aGUAgMG-n-Q5GT6HmeAB0807PVBlZtqHc2atzMhtc4YeFtWx-gz4cI6iuynfsQ3bgSy9cdIoTua4fpVaCer-NDowl0FTMBbjPHnLTRRUZPhPQFbKA)
Therefore, leak will empty the full tank in 20 h.
- There are two tanks A and B to fill up a water tank. The tank can be filled in 40 min, if both taps are on. The same tank can be filled in 60 min, if tap A alone is on. How much time will tap B alone take, to fill up the same tank?
Solution: Part filled by tap A in 1 min = 1/60
Let tap B fills the tank in x min
Then, part filled by tap, B in 1 min = 1/x
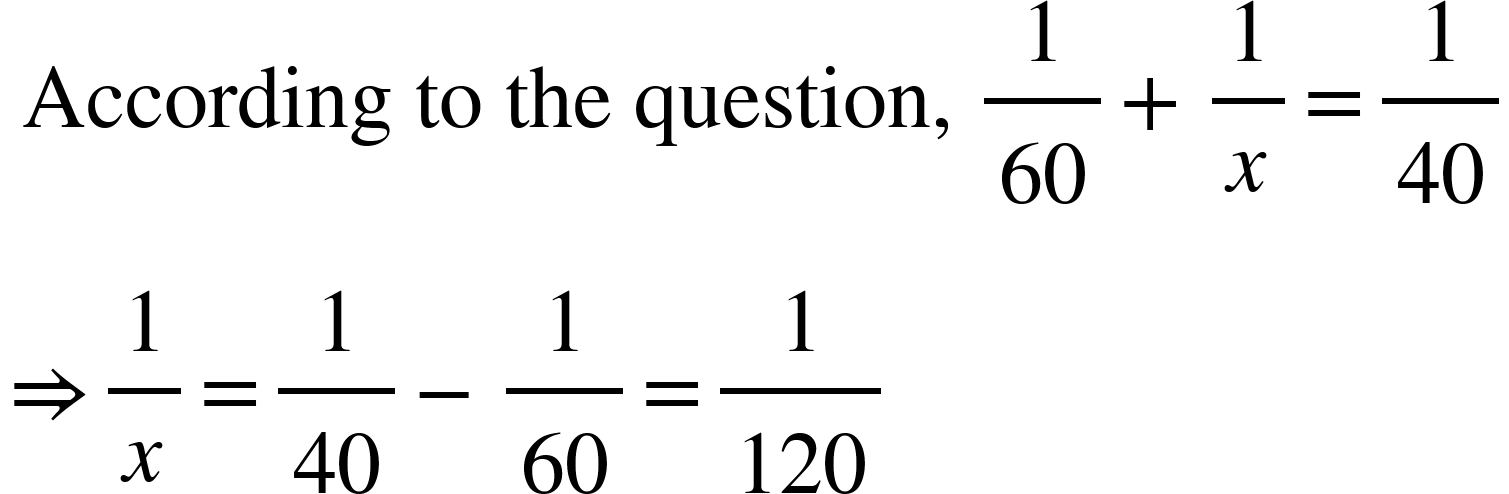
Therefore, Tap B can fill the tank in 120 min.
- Inlet A is four times faster than inlet B to fill a tank. If A alone can fill it in 15 min, how long will it take if both the pipes are opened together?
Solution: Time taken by A to fill the tank, m = 15 min
Therefore, time taken by B to fill the tank, n = 15 x 4 = 60 min
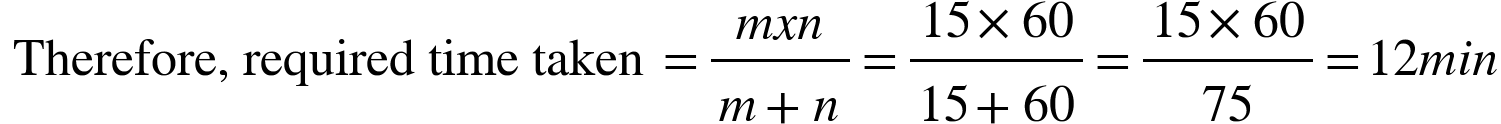
5. A tap having diameter 'd' can empty a tank in 40 min. How long another tap having diameter '2d' take to empty the same tank?
Solution: Area of tap ∞ work done by pipe
When diameter is doubled, area will be four times. So, it will work four times faster.
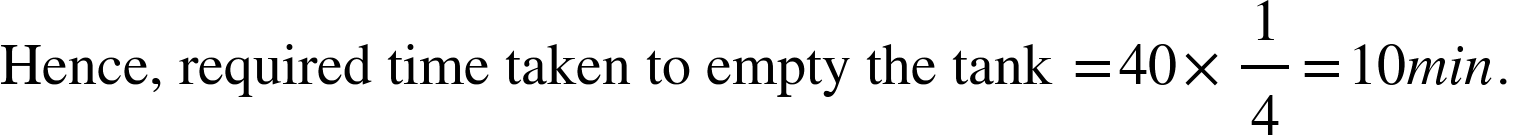
Clock
A clock is an instrument which displays time divided into hours, minutes and seconds.
A clock mainly consists of four components.
Dial
A clock is a circular dial. The periphery of the dial is numbered 1 through 12 indicating the hours in a 12 h cycle. The circumference of a dial is divided into 60 equal spaces.
Every clock has mainly two hands, one is smaller and other is bigger. The smaller hand is slower the and the bigger hand is faster.
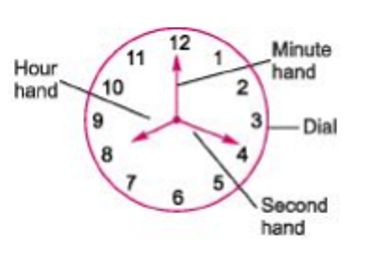
Hour Hand
The smaller or slower hand of a clock is called the hour hand. It makes two revolutions in a day. Minute Hand
The bigger or faster hand of a clock is called the minute hand. It makes one revolution in every hour.
Second Hand
Second hand indicates seconds on a circular dial. It makes one revolution per minute.
Note:
In 1 h minute hand covers 60 min spaces whereas the hour hand covers 5 min spaces Therefore, minute hand gains (60 - 5) = 55 min in 1 h
Important Points Related to Clock
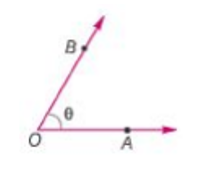
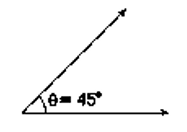
- In 1 h, both hands coincide once (i.e., 0° apart)
For example: Between 3 and 4'o clock, hands are together as shown in adjacent figure

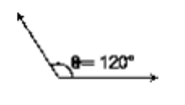
2. In 12 h, both hands coincide 11 times (between 11 and 1'o clock they coincide once) and in a day both hands coincide 22 times.
For example, between 11 and 1'o clock, hands are together as shown in adjacent figure.

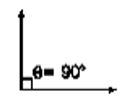
3. If two hands are at 90 ° they are 15 min spaces apart. This happens twice in 1 h. In a period of 12 h, the hands are at right angle 22 times (2 common positions) and in a day both hands are at right angle 44 times.
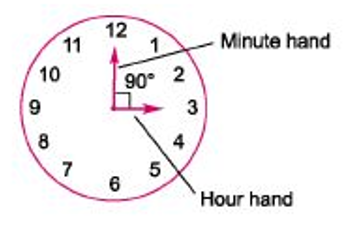
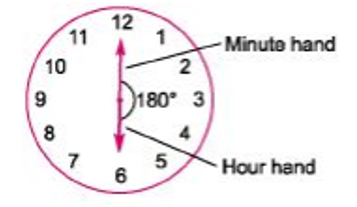
4. If two hands are in opposite direction. (i.e., 180°apart), then they are 30 min spaces apart. This happens once in 1 h. In a period of 12 h both hands are in opposite direction 11 times and in a day both hands are in opposite direction 22 times.
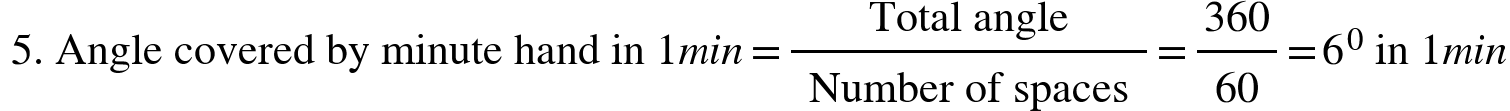
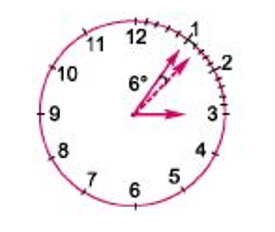
6. Angle covered by hour hand in 1 min.


7. From point 5 and 6, we can say that the minute hand goes ahead by 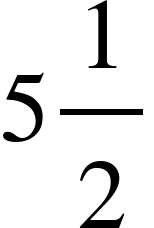 in comparison to hour band.
in comparison to hour band.
Concept of Slow or Fast Clocks
If a watch/clock indicates 9: 15, when the correct time is 9, then it is said to be 15 min too fast.
On the other hand, if the watch/clock indicates 6: 45, when the correct time is 7, then it is said to be 15 min too slow.
Examples:
- A clock gains 10 s in every 3 h. If the clock was set right at 4:00 am on Monday morning, then the time it will indicate on Tuesday evening at 7:00 pm.
Solution: Difference of time between 4.00 am on Monday to 7.00 pm Tuesday
24 + 12 + 3 = 39 h
- At what time between 4 o'clock and 5 o'clock, will the hands of a clock be together?
Solution: At 4 o'clock, the hour hand is at 4 and the minute hand is at 12.
It means that they are 20 min spaces apart.
To be together, the minute hand must gain 20 min over the hour hand.
As we know, 55 min is gained by minute hand in 60 min


3. At what time between 3 o'clock and 4 o'clock, will the hands of a clock be in opposite directions?
Solution: At 3 o'clock, the hour hand is at 3 and the minute hand is at 12.
It means that the two hands are 15 min spaces apart. But to be in opposite directions, the hands must be 30 min spaces apart.
Therefore, the minute hand will have to gain (30 + 15) = 45 min spaces over the hour hand.
Therefore 55 min spaces are gained in 60 min
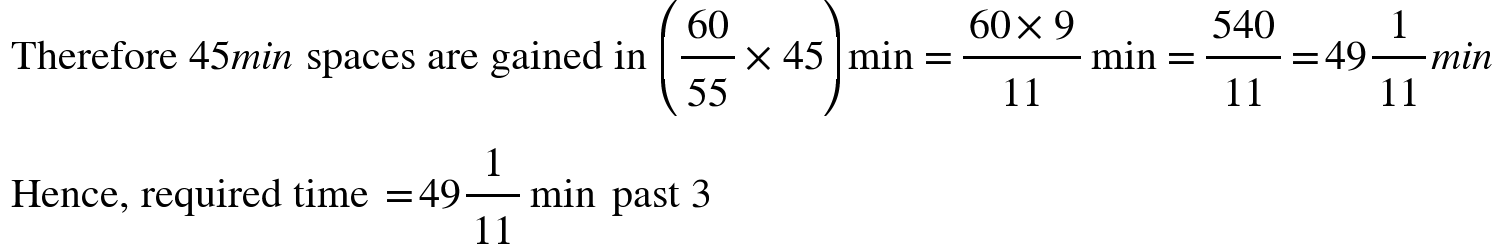
4. At what point of time after 3 O' clock, hour hand and the minute hand are at right angles for the first time?

Given that, n = 3
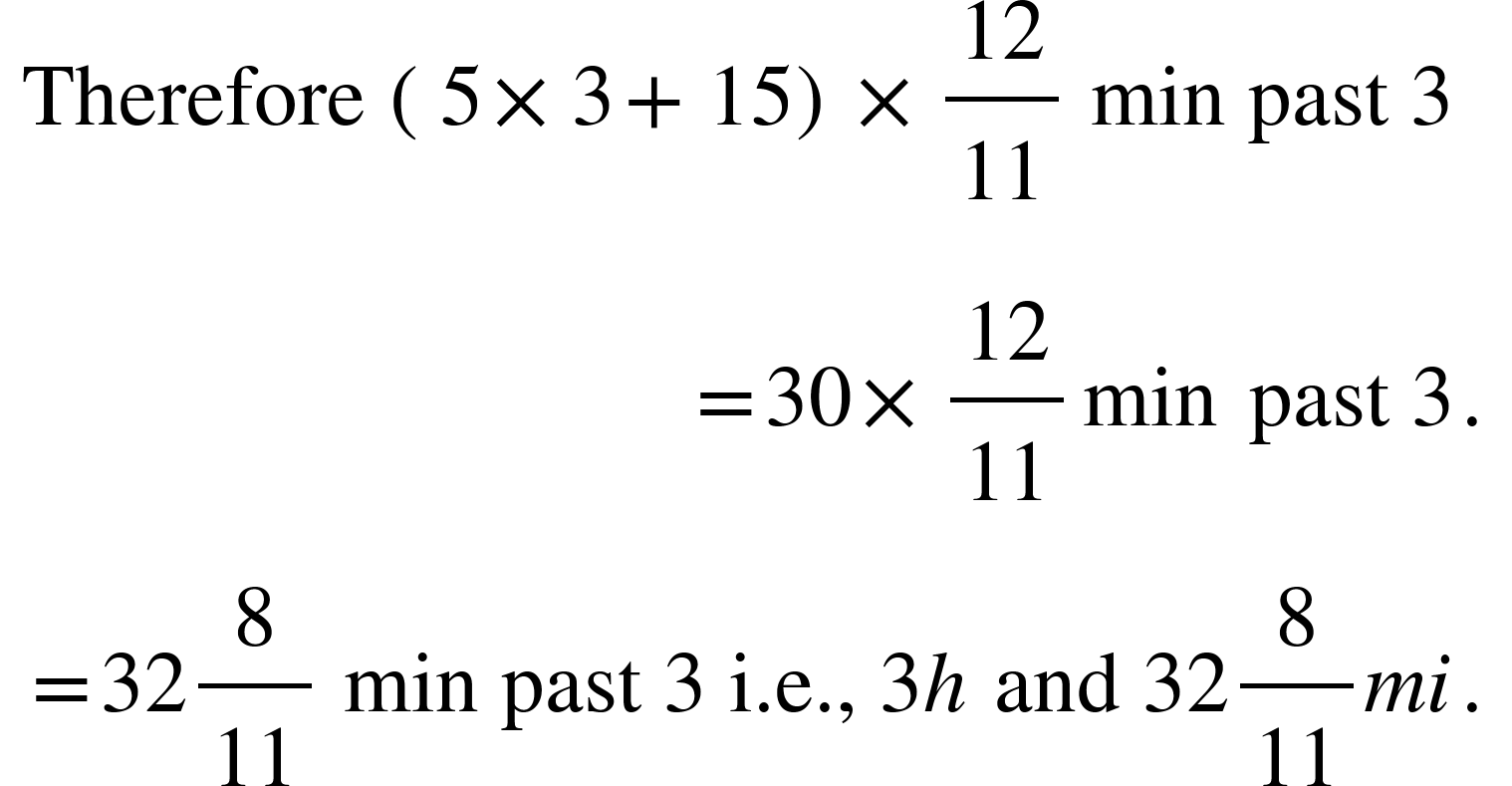
5. At what time between 9 o'clock and 10 o'clock, will the hands of a clock be in the same straight line but not together?
Solution: At 9 o' clock, the hour hand is at 9 and the minute hand is at 12.
It means that the two hands are 15 min spaces apart.
To be in the same straight line (but not together), they will be 30 min space apart.
... The minute hand will have to gain (30-15) = 15 min spaces over the hour hand.
As we know, 55 min spaces are gained in 60 min.
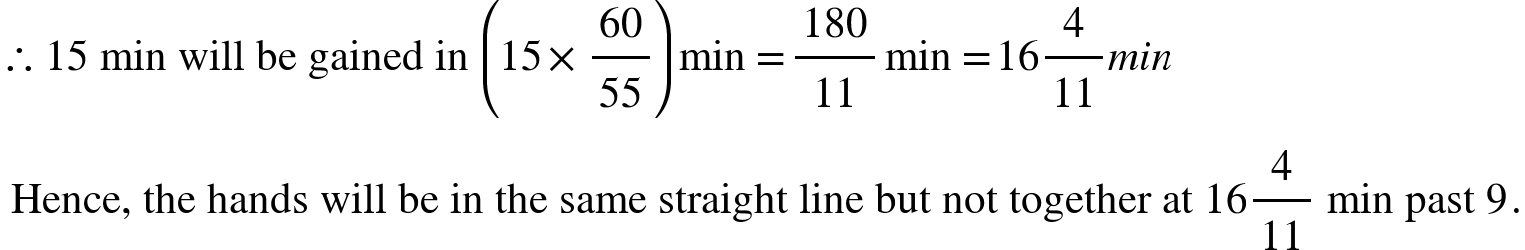
Calendar
A calendar is chart or series of pages showing the days, weeks and months of a particular year. A calendar consists of 365 or 366 days divided into 12 months.
Ordinary Year
A year having 365 days is called an ordinary year (52 complete weeks + 1 extra day = 365 days)
Leap Year
A leap year has 366 days (the extra day is 29th of February) (52 complete weeks + 2 extra days =366 days.)
A leap year is divisible by 4 except for a century. For a century to be a leap year it must be divisible by 400. e.g.,
- Years like 1988, 2008 are leap year (divisible by 4).
- Centuries like 2000, 2400 are leap year (divisible by 400).
- Years like 1999, 2003 are not leap year (not divisible by 4).
- Centuries like 1700, 1800 are not leap year (not divisible by 400).
- In a century, there is 76 ordinary year and 24 leap years.
Odd Days
- Extra days, apart from the complete weeks in a given period are called odd days.
- Number of days in an ordinary year = 365 = (52 x 7) + 1 = 52 weeks + 1 odd day
- An ordinary year has 1 odd day
- Number of days in a leap year = 366 = (52 x 7) + 2 = 52 weeks + 2 days
- while a leap year has 2 odd days.
- Number of days in a century (100 yr) = 76 ordinary years + 24 leap years = 76x1+ 24x2) =124 =17x7+5 =17 week+ 5 odd days
- Therefore, 100yrs has 5 odd days.
- Number of odd days in 200 yr = 5x2=10 days = 1 week + 3 days = 3 odd days
- Number of odd days in 300 yr = 5 x 3 = 15 days = 2 weeks + 1 day = 1 odd day
- Number of odd days in 400 yr = (5 x 4 +1) days =21 days = 3 weeks = 0 odd days
- As 400th is a leap year, therefore 1 more day has been taken
- Similarly, each one of 800 yr, 1200 yr, 1600 yr, 2000 yr, 2400 yr etc., has no odd days.
- Remember the adjacent table for the number of odd days in different months of an year.
- In an ordinary year, February has no odd days, but in a leap year, February has one odd day.
- The 1 st day of a century must be Tuesday, Thursday or Saturday.
- The last day of a century cannot be Tuesday, Thursday or Saturday.
Day Gain/Loss
Ordinary Year (± 1 day)
- When we proceed forward by 1 yr, then 1 day is gained.
For example: 9th August 2013 is Friday, then 9th August 2014 has to be Friday +1 = Saturday.
- When we move backward by 1 yr, then 1 day is lost.
- For example: 24th December 2013 is Tuesday, then 24th December 2012 has to be Tuesday -1 = Monday.
Leap Year (+ 2 days)
- When we proceed forward by 1 leap year, then 2 days are gained.
For example: If it is Wednesday on 25th December 2011, then it would be Friday on 25th December 2012 [Wednesday + 2] because 2012 is a leap year.
- When we move backward by 1 leap year, then 2 days are lost.
For example: If it is Wednesday on 18th December 2012, then it would be Monday on 18th December 2011. [Wednesday -2] because 2012 is a leap year.
Exception
• The day must have crossed 29th February for adding 2 days otherwise 1 day.
For example: If 26th January 2011 is Wednesday, 26th January 2012 would be Wednesday + 1 = Thursday (even if 2012 is leap year, we have added + 1 day because 29 February is not crossed).
If 23rd March 2011 is Wednesday, then 23rd March 2012 would be Wednesday + 2 = Friday (+ 2 days 29th February of leap year is crossed)
To Find a Particular Day on the Basis of Given Day and Date
Following steps are taken into consideration to solve such questions
Step I: Firstly, you have to find the number of odd days between the given date and the date for which the day is to be determined.
Step II: The day (for a particular date) to be determined, will be that day of the week which is equal to the total number of odd days and this number is counted forward from the given day, in case the given day comes before the day to be determined.
But, if the given day comes after the day to be determined, then the same counting is done backward from the given day.
To Find a Particular Day without Given Date and Day
Following steps are taken into consideration to solve such questions
Step I: Firstly, you have to find the number of odd days up to the date for which the day is to be determined.
Step II: Your required day will be according to the following conditions
(a) If the number of odd days = 0, then required day is Sunday.
(b) If the number of odd days = 1, then required day is Monday.
(c) If the number of odd days = 2, then required day is Tuesday.
(d) If the number of odd days = 3, then required day is Wednesday.
(e) If the number of odd days = 4, then required day is Thursday.
(f) If the number of odd days = 5, then required day is Friday. (g) If the number of odd days = 6, then required day is Saturday.
Examples:
- 14 How many days are there in x weeks x days?
Solution: Number of days in x weeks = 7x + x
... Total number of days is x week x days = 7x + x = 8x days
- Find the day of the week on 26th January 1950.
Solution: Number of odd days up to 26th January, 1950
= Odd days for 1600 yr + Odd days for 300 yr + Odd days for 49 yr + Odd days of 26 days of January 1950 = 0 + 1 + (12 X2 +37) + 5 = 0 + 1 + 61 + 5 = 67 days = 9 weeks + 4 days = 4 odd days
Therefore, It was Thursday on 26th January 1950.
- January 3, 2007 was Wednesday. What day of the week fell on January 3, 2008?
Solution: The year 2007 is an ordinary year, so it has 1 odd day.
3rd day of the year 2007 was Wednesday.
... 3rd day of the year 2008 will be one day beyond the Wednesday.
Hence, it will be Thursday.
- What was the day of the week on 17th August, 2010?
Solution: Period up to 17th August, 2010 = (2009yr + Period from 1.1.2010 to 17.8.2010)
Counting of odd days odd days in 1600 yr = 0 Odd days in 400 yr = 0
9 yr = (2 leap years + 7 ordinary years) = (2x2+7xl) = l week + 4 days = 4 odd days
Number of days between 1.1.2010 to 17.8.2010
January + February + March + April + May + June + July + August
= (31 +28 + 31+30 + 31 + 30 + 31 + 17) days
= 229 days = 32 weeks + 5 odd days
Total number of odd days = (0 + 0 + 4 + 5) days = 9 days = 1 week + 2 odd days
Hence, the required day is Tuesday
- If 5th March, 1999 was Friday, what day of the week was it on 9th March 2000?
Solution: 5th March, 1999 is Friday.
Then, 5th March 2000 = Friday + 2 = Sunday.
{2000 is leap year and it crosses 29th Feb 2000, so 2 is taken as odd day}
... 5th March 2000 = Sunday. Then, 9th March 2000 = Thursday.
Boats and streams
It is an application of concepts of speed, time and distance. Speed of river flowing either aides a swimmer (boat), while travelling with the direction of river or it opposes when travelling against the direction of river.
Still Water:
If the speed of water of a river is zero, then water is considered to be still water.
Stream Water
If the water of a river is moving at a certain speed, then it is called as stream water.
Speed of Boat:
Speed of boat means speed of boat (swimmer) in still water. In other words, if the speed of a boat (swimmer) is given, then that particular speed is the speed in still water.
Downstream Motion:
If the motion of a boat (swimmer) is along the direction of stream, then such motion is called downstream motion.
Upstream Motion:
If the motion of a boat (swimmer) is against the direction of stream, then such motion is called upstream motion.
Formulae related to Boats and Strems:
- If the speed of a boat in still water is a miles/h and speed of the stream is b miles/h, then
- Speed downstream = (a + b) miles/h
- Speed upstream = (a – b) miles/h
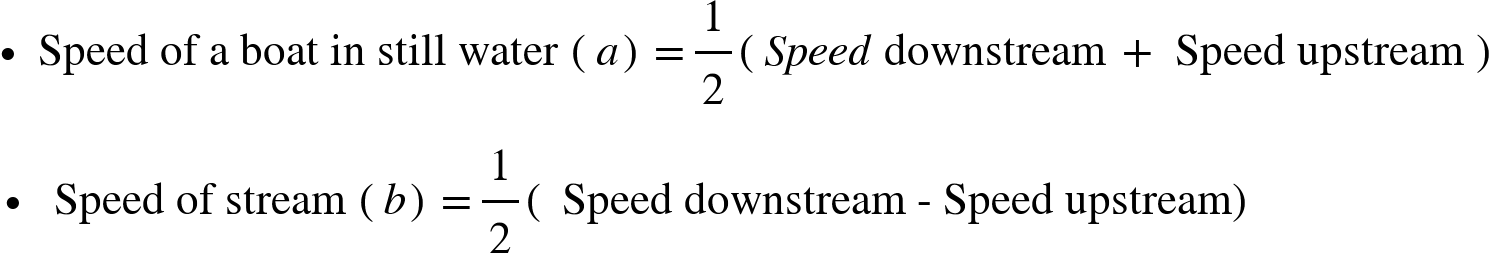
Examples:
- If the speed of a boat in still water is 10 miles/h and the rate of stream is 5 miles/h, then find upstream speed of the boat.
Sol. Given,
speed of a boat = a = 10 miles/h Speed of stream = b = 5 miles/h
Hence, Speed upstream = a – b = 10 - 5 = 5 miles/h.
- Kevin can row a certain distance downstream in 24 h and can return the same distance in 36 h. If the stream flows at the rate of 12 miles/h, then find the speed of Kevin in still water.
Solution:
- Let the Kevin’s speed in still water = a
- Then, Kevin's speed downstream = (a + 12)
- Kevin's speed upstream = (a - 12)
Given that,
- Distance travelled downstream = Distance travelled upstream
- 24 (a + 12) = 36 (a - 12)
- 2 (a + 12) = 3 (a – 12)
- 2a + 24 = 3a – 36
- 3a – 2a = 36 + 24
- a = 60 miles/h
- A boat's speed in still water is 12 miles/h, while river is flowing with a speed of 4 miles/h and time taken to cover a certain distance upstream is 6 h more than time taken to river the same distance downstream. Find the distance.
Solution: Let the distance = d
Boat’s rate downstream = 12 + 4 = 16 miles/h
Boat’s rate upstream = 12 – 4 = 8 miles/h
Difference between the time = Time taken by boat to travel upstream - Time taken by boat to travel downstream
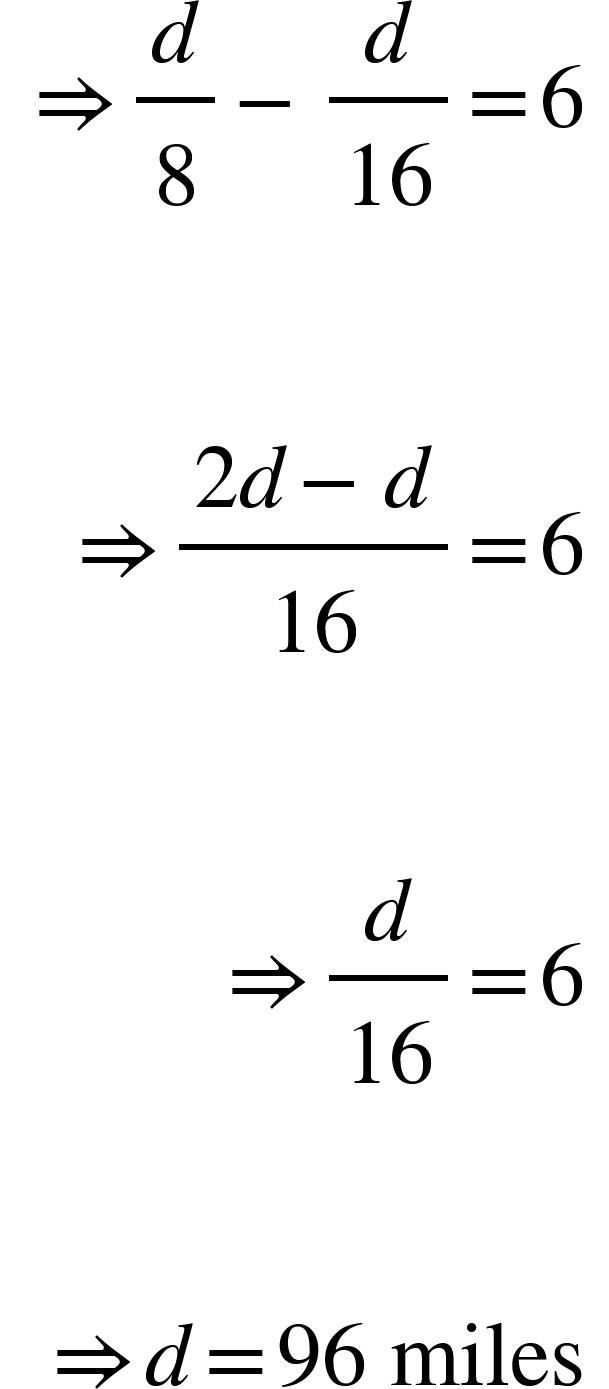
4. Andrew can row 36 miles/h in still water. It takes him twice as long to row up as to row down the river. Find the rate of stream.
Solution:
- Let rate of stream be a miles/h.
According to the question,
- 36 + a = 2(36 - a)
- 36 + a = 72 - 2a
- 3a = 72 - 36 = 36
- a = 36/3 = 12 miles/h
5. A boatman takes twice as long to row a distance against the stream as to row the same distance with the stream. Find the ratio of speeds of the boat in still water and the stream.
Solution:
- Let boatman's speed upstream p
- His speed downstream = 2p
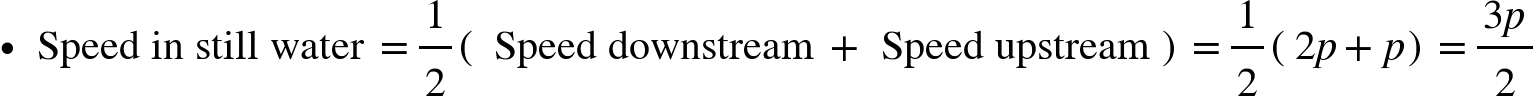

When two or more persons make an association and invest money for running a certain business and after certain time receive profit in the ratio of their invested money and time period of investment, then such an association is called partnership and the persons involved in the partnership are called partners.
Partnership is of Two Types
Simple Partnership
If all partners invest their different capitals (money) for the same time period or same capital for different time period then their profit or loss is in the ratio of their investments or time period of investment then such a partnership is called simple partnership
Compound Partnership
If all partners invest their different capitals (money) for different time period, then their profit not only depends on their investments but also on the time period of their investment, then such a partnership is called compound partnership
Partners are of Two Types
Active or Working Partner
A partner who not only invests money, but also take part in the business activities for which he draws a defined salary or gets some share from profit before its division is called an active partner.
Sleeping Partner
A partner who only invests money and does not take part in business activities is called sleeping partner.
Ratio of division of gains:
- When the investments made by all the partners are for the same time period, then gain or loss is distributed amongst them in the ratio of their investments,
Suppose A and B invest $ x and $ y respectively for a year in a business, then at the end of the year: (A’s share of profit): (B’s share of profit) = x: y
- When investments are of different time periods, then equivalent capitals are calculated for a unit of time by taking (capital x number of units of time). Now, gain or loss is divided in the ratio of these capitals.
Suppose A invests $ x for p months and B invests $ y for q months, then (A’s share of profit): (B’s share of profit) = xp: yq.
Examples:
- P and Q entered a partnership for 3 yr. At the start of the business, they invested $ 13000 and $ 25000, respectively. At the end of 3 yr their total profit was $ 76000. What will be share of Q out of this profit?
Solution: P’s share: Q’s share = Ratio of their investments
= 13000: 25000
= 13: 25
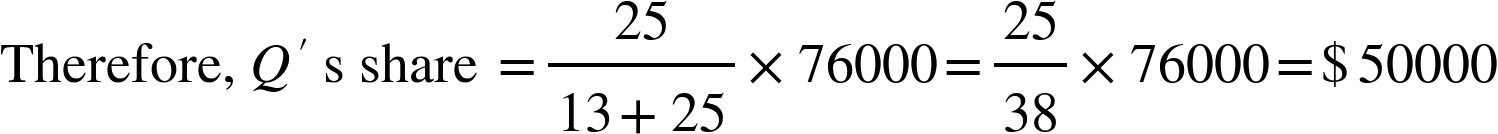
2. A, B and C invested their capitals in the ratio of 5: 6: 8. At the end of the business, they received the profits in the ratio of 5: 3: 1. Find the ratio of time for which they contributed their capitals.
Solution: Here P1: P2: P3 = 5: 3: 1 and x1: x2: x3 = 5: 6: 8

3. A and B together start a business by investing in the ratio of 4: 3. If 9% of the total profit goes to charity and A's share is $ 1196, find the total profit.
Solution: Let total profit = x


4. A and B started a business with $ 20000 and $ 35000 respectively. They agreed to share the profit in the ratio of their capital. C joins the partnership with the condition that A, B and C will share profit equally and pays $ 220000 as premium for this, to be shared between A and B. This is to be divided between A and B in the ratio of
Solution: Ratio of total capital of A and B = 20000 x 12: 35000 x 12
= 240000: 420000
Now, C gives $220000 to both to make the capital equal.

If A takes $ 200000 and B takes $ 20000 from C, then both have the equal capital
Therefore, required ratio of divided amount = 200000: 20000 = 20: 2 =10: 1
4. P, Q and R hire a meadow for $ 2920. P puts 10 cows for 20 days; Q puts 30 cows for 8 days and R puts 16 cows for 9 days. Find the rent paid by R.
Solution: Ratio of rents to be paid by P, Q and R
Ratio of monthly equivalent = (10 x 20): (30 x 8): (16 x 9)
= 200: 240: 144
= 25: 30: 18