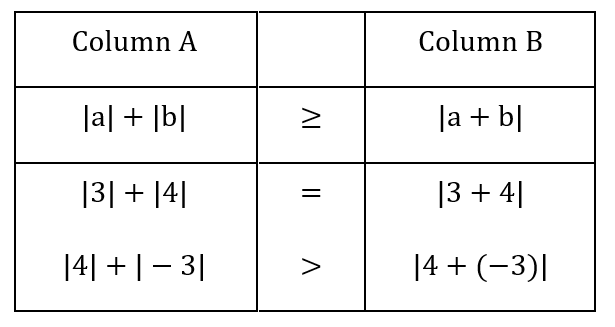
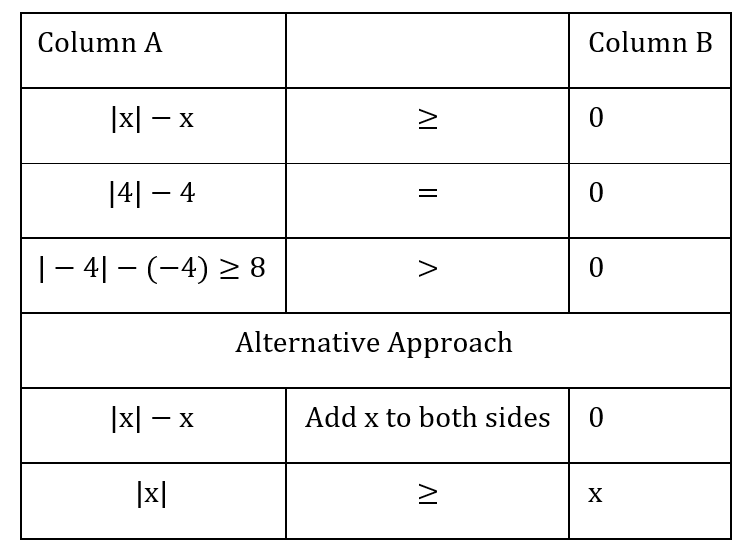
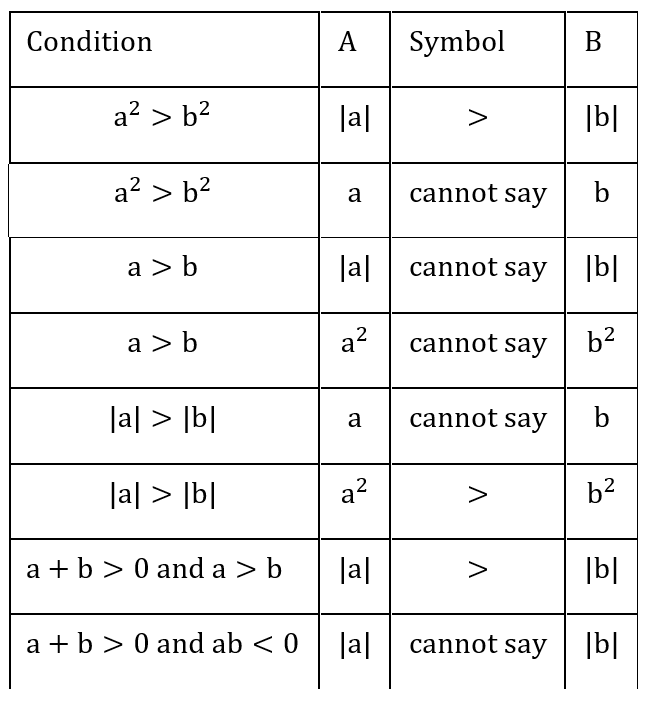
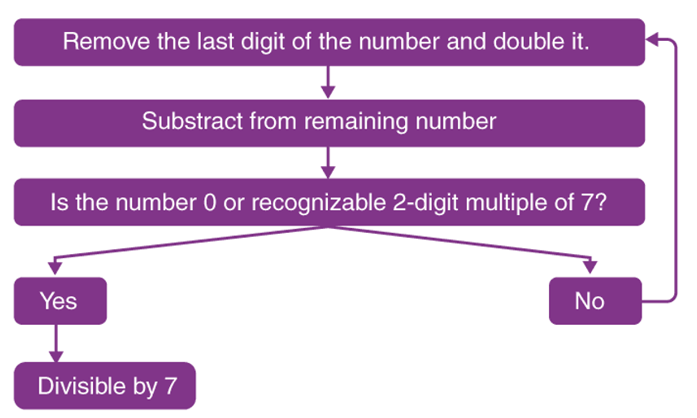
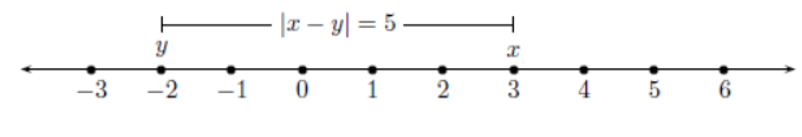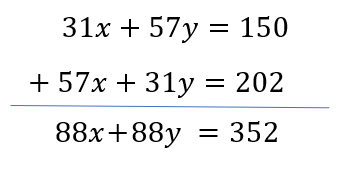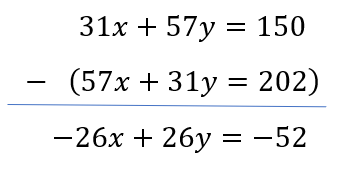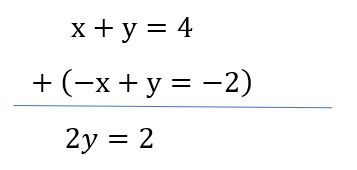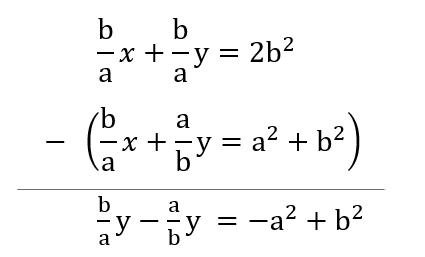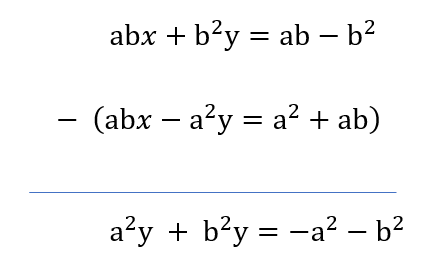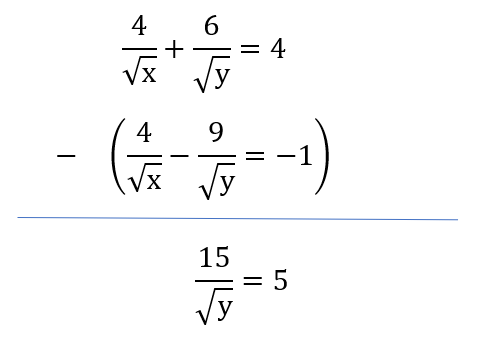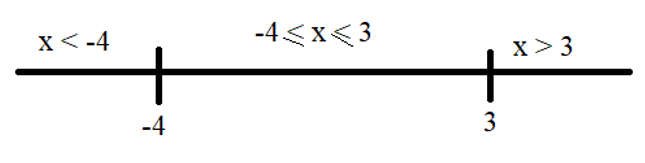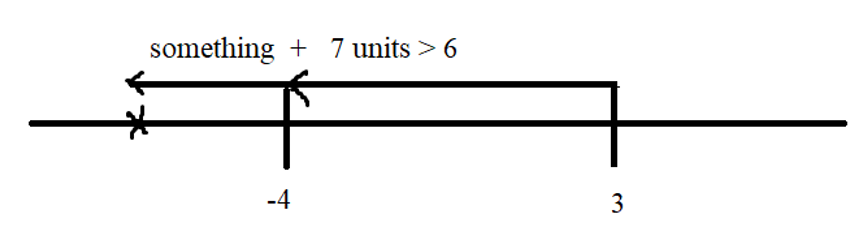1 Averages - Trick #13
N/A
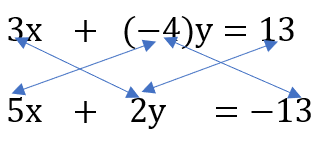
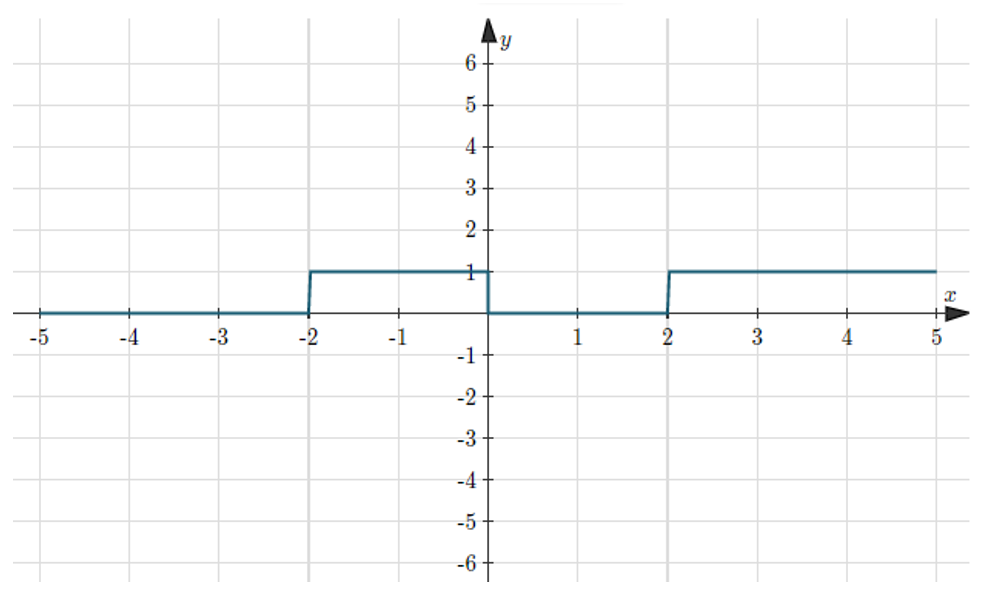
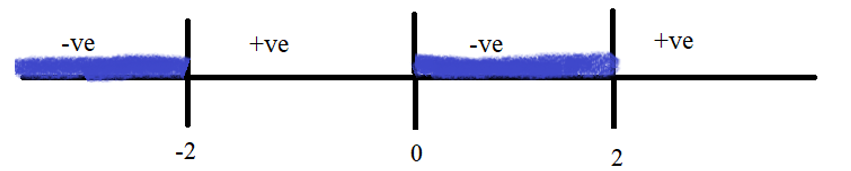
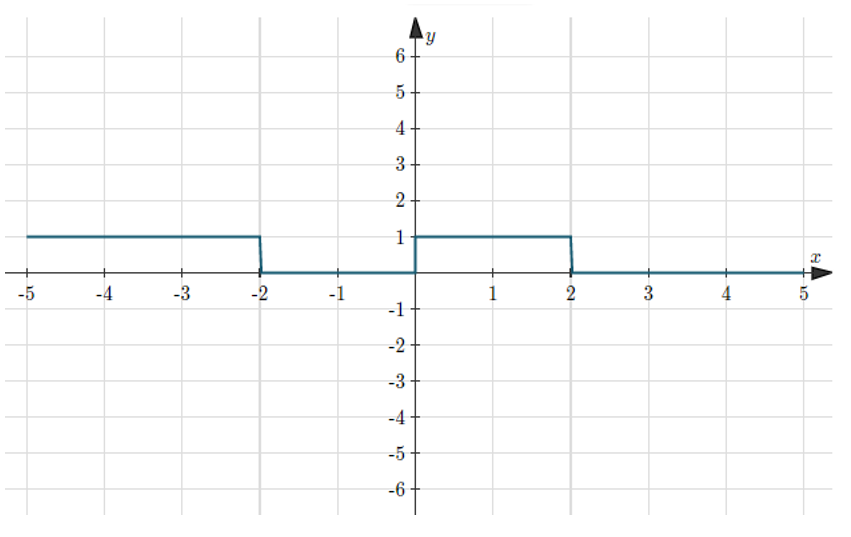
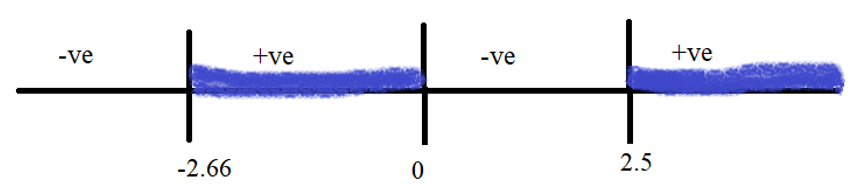
\&space;numbers,\&space;the\&space;average\&space;of\&space;first\&space;n\&space;numbers\&space;is\&space;'F'&space;and\&space;the)
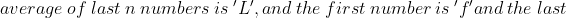
)
Example:
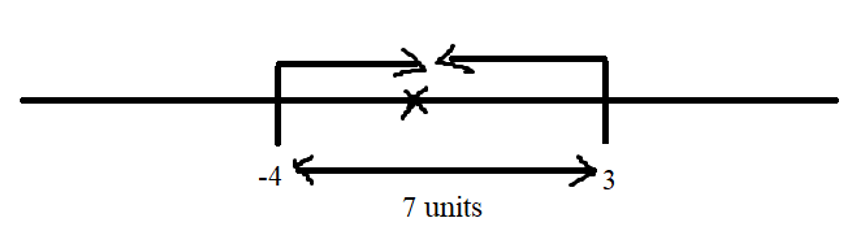
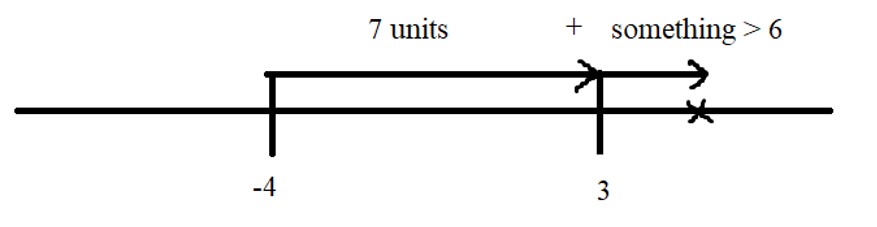
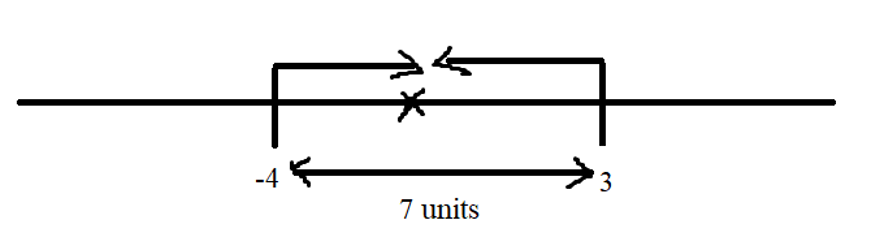
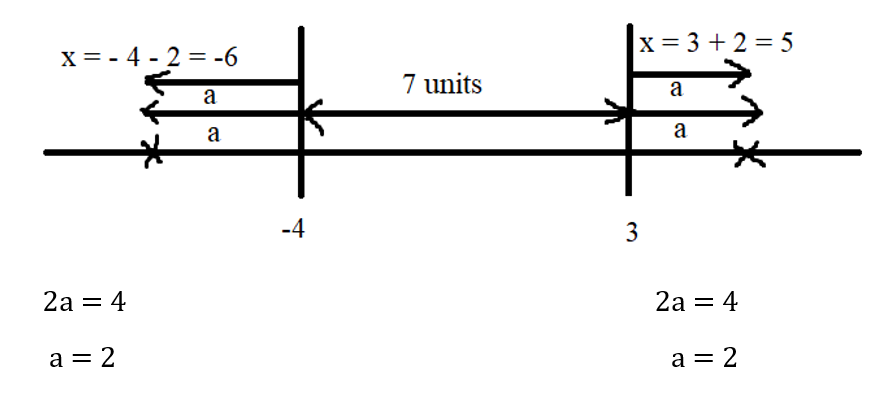
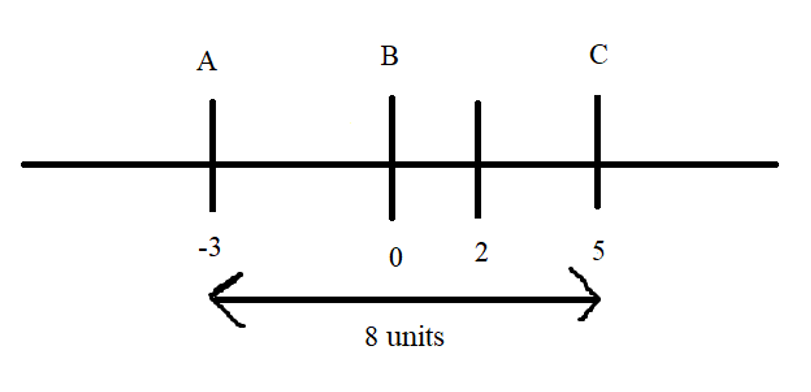
Out of four numbers the average of the first three is 16 and that of the last three is 15. If the last number is 20 then the first number is?
Solution:
Normal Method:
\&space;Let\&space;three\&space;numbers\&space;be\&space;a,b\&space;and\&space;c\&space;respectively.\)
\)
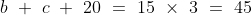
)
\&space;-\&space;(ii),\)
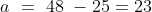
Shortcut Method:
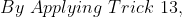
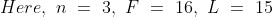
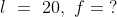
)
)
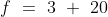
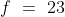
2 Averages - Trick #14
N/A
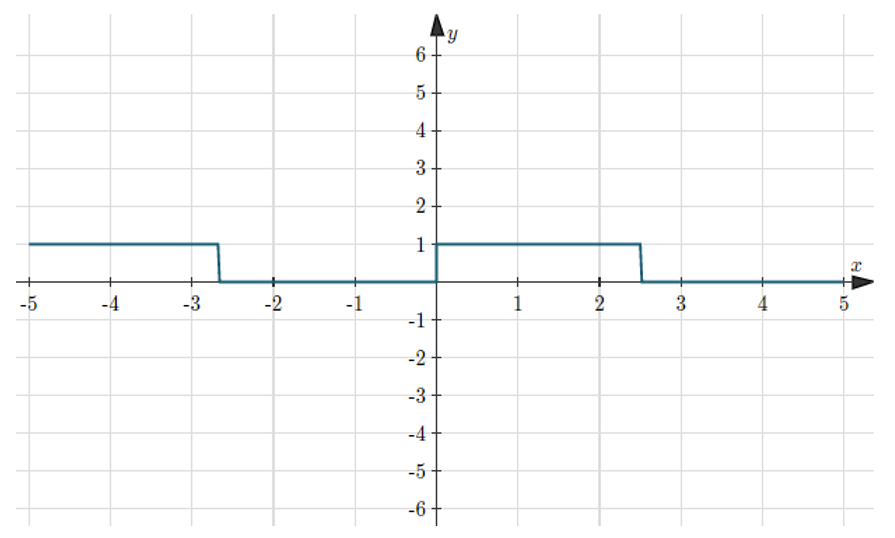
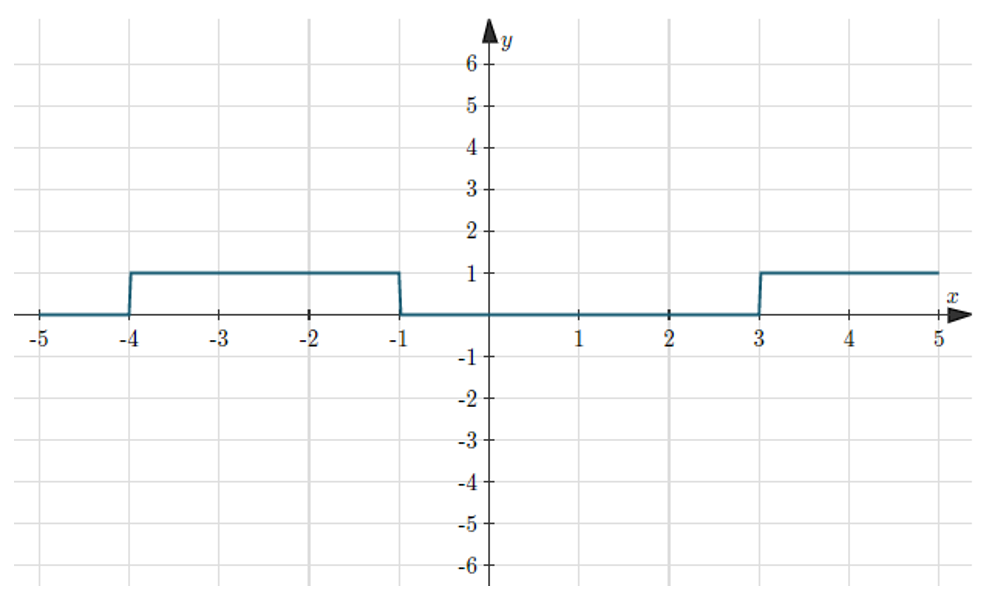
If in the group of N persons, a new person comes at the place of a person of ‘T’ years, so that average age, increases by ‘t’ years
Then, the age of the new person = T + N.t
If the average age decreases by ‘t’ years after entry of new person, then the age of the new person = T – N.t
Example:
3 years ago, the average age of a family of 5 members was 17 years. A baby having been born, the average age of the family is the same today. The present age of the baby is?
Solution:
Normal Method:
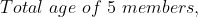
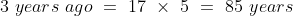
=100\&space;years\)

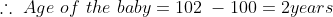
Shortcut Method:
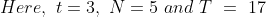
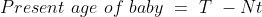
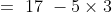
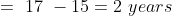
3 Averages - Trick #15
N/A
The average age of a group of N students is ‘T’ years. If ‘n’ students join, the average age of the group increases by ‘t’ years, then average age of new students
t)
If the average age of the group decreases by ‘t’ years, then average age of new students
t)
Example-1:
The mean of 9 observations is 16. One more observation is included and
the new mean becomes 17. The 10th observation is?
Solution:
Normal Method:
Sum of Ten observations – Sum of nine observations = Tenth observation
 Tenth observation = 10 × 17 – 16 × 9 = 170 – 144 = 26
Tenth observation = 10 × 17 – 16 × 9 = 170 – 144 = 26
Shortcut Method:
By Applying Trick 15,
Here, N = 9, T = 16 n = 1, t = 1
t)
\times1)

Example-2:
The average of 100 numbers is 44. The average of these 100 numbers and 4
other new numbers are 50. The average of the four new numbers will be?
Solution:
By Applying Trick 15,
Here, N = 100, T = 44, n = 4, t = 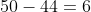
t)
\times6)
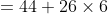

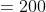

4 Averages - Trick #16
N/A
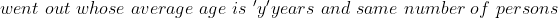
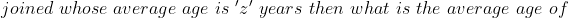
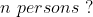
}{n}\right\}\mathrm{\&space;years})
Example:
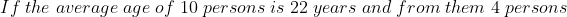
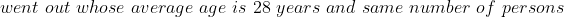
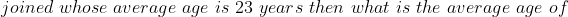
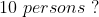
Solution:
By Applying Trick 16,
Here, n = 10, m = 4, x = 22, y= 28 and z = 23
}{n})
}{10}\right))
}{10}\right))
)
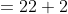
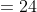
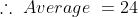
5 Averages - Trick #17
N/A
If in a group, one member is replaced by a new member, then, \&space;\pm\&space;xn)
\&space;or\&space;decrease\&space;(-)&space;in&space;average)
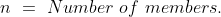
Example-1:
The average weight of 8 persons increases by 2.5 kg when a new person
comes in place of one of them weighing 65 kg. The weight of the new
person is?
Solution:
By Applying 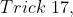
Here, x = 2.5, n = 8
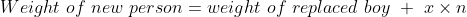
)
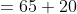
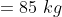
Example-2:
In a class, there are 40 boys and their average age is 16 years. One boy, aged 17 years, leaving the class and another joining, the average age becomes 15.875 years. The age of the new boy is?
Solution:

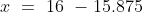
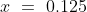
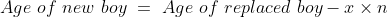
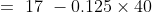
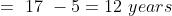
Example-3:
In a class there are 30 boys and their average age is 17 years. On one boy aged 18 years leaving the class and another joining, the average age becomes 16.9 years. The age of new boy is?
Solution:
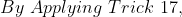
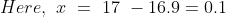
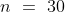
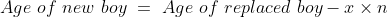

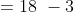
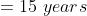
6 Averages - Trick #18
N/A
\&space;of\&space;added\)
\pm\&space;x\&space;(n\&space;+\&space;1))
\&space;or\&space;decrease\&space;(-)&space;in\&space;average\&space;age\&space;(or\&space;income))
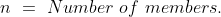
Example-1:
Average weight of 25 students of a class is 50 kg. If the weight of the class teacher is included, the average is increased by 1 kg. The weight of the teacher is?
Solution:
By Applying Trick 18,
Here, Average = 50,
n = 25,
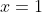
\)
= 50 + 1 (25 + 1)
= 50 + 26
= 76 kg
Example-2:
The mean weight of 34 students of a school is 42 kg. If the weight of the teacher be included, the mean rises by 400 grams. Find the weight of the teacher (in kg)?
Solution:
By Applying Trick 18,
Here, Average = 42,
n = 34,
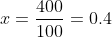
\)
= 42 + 0.4 (34 + 1)
= 42+ 14
= 56 kg
The average age of four brothers is 12 years. If the age of their mother is also included, the average is increased by 5 years. The age of the mother (in years) is?
Solution:
By Applying Trick 18,
Here, Average = 12,
x = 5, n = 4
Age of mother = Average + x (n+1)
= 12 + 5 (4 + 1)
= 12 + 25
= 37 years
7 Averages - Trick #19
N/A
If a member leaves the group, then income (or age) of left member = \&space;\pm\&space;x\&space;(n\&space;-&space;1))
where, x = increase (+) or decrease (–) in average income (or age) n = Number of members.
Example:
The average of five numbers is 140. If one number is excluded, the average of the remaining four numbers is 130. The excluded number is?
Solution:
By Applying Trick 19,
Here, Average = 140,
x = (140 – 130) = 10
n = 5
Excluded number = Average + x (n – 1)
= 140 + 10 × 4
= 180
8 Averages - Trick #20
N/A
If average of n numbers is m later on it was found that a number ‘a’ was misread as ‘b’.
}{n})
Example-1:
The average of a collection of 20 measurements was calculated to be 56 cm.
But later it was found that a mistake had occurred in one of the measurements which was recorded as 64 cm., but should have been 61 cm.
The correct average must be
Solution:
By Applying Trick 20,
Here, n = 20, m = 56
a = 61, b = 64
}{n})
)
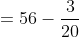
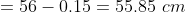
Example-2:
The average marks of 100 students were found to be 40. Later on, it was discovered that a score of 53 was misread as 83. Find the correct average corresponding to the correct score.
Solution:
By Applying Trick 20,
Here, n = 100, m = 40
a = 53, b = 83
}{n})
)
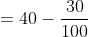
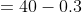
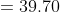
Example-3:
The average weight of a group of 20 boys was calculated to be 89.4 kg and it was later discovered that one weight was misread as 78 kg instead of 87kg. The correct average weight is?
Solution:
By Applying Trick 20,
Here, n = 20, m = 89.4
a = 87, b = 78
}{n})
)
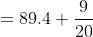
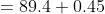
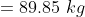
9 Averages - Trick #21
N/A
If the average of n numbers is m later on it was found that two numbers a and b misread as p and q.
}{n})
Example-1:
The mean of 50 numbers is 30. Later it was discovered that two entries were wrongly entered as 82 and 13 instead of 28 and 31. Find the correct mean.
Solution:
By Applying Trick 21,
Here, n = 50, m = 30
a = 28, b = 31
p = 82, q = 13
}{n})
}{50})
)
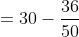
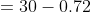
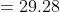
Example-2:
The average of marks of 14 student was calculated as 71. But it was later found that the marks of one student had been wrongly entered as 42 instead of 56 and of another as 74 instead of 32. The correct average is?
Solution:
By Applying Trick 21,
Here, n = 14, m = 71
a = 56, b = 42
p = 32, q = 74
}{n})
}{50})
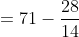
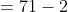

Example-3:
Mean of 10 numbers is 30. Later on, it was observed that numbers 15, 23 are wrongly taken as 51, 32. The correct mean is?
Solution:
By Applying Trick 21,
Here, n = 10, m = 30
a = 15, b = 23
p = 51, q = 32
}{n})
}{10})
)
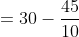
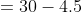
10 LCM and HCF - Trick #22
N/A
Least common Multiple (L.C.M):
The least number which is divisible by two or more given numbers, that least number is called L.C.M. of the numbers.
Ex: L.C.M. of 3,5,6 is 30, because all 3 numbers divide 30, 60, 90, ...... and soon perfectly and 30 is minimum of them.
Highest Common Factor (H.C.F):
It is also called Greatest common Divisor (G.C.D). When a greatest number divides perfectly the two or more given numbers then that number is called the H.C.F. of two or more given numbers.
Ex: The H.C.F of 10, 20, 30 is 10 as they are perfectly divided by 10,5 and 2 and 10 is highest or greatest of them.
Factor and Multiple:
If a number m, divides perfectly second number n, then m is called the factor of n and n is called the multiple of m.
Trick #22
Finding LCM by Large Number method:
Case - 1:
LCM of 6, 12, 24, 48
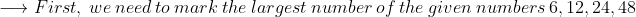
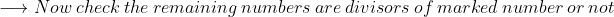
In this case remaining numbers 6, 12, 24 are divisors of 48 then the LCM of the numbers is 48.
Case - 2:
LCM of 5, 10, 20, 50
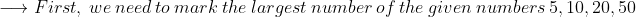
In this case only 5, 10 are divisors of 50 then eliminate 5, 10 from the list. 20, 50

Note: If there is no common factor between two numbers, then L.C.M. will be the product of both numbers.
100 is the common multiple. Then the LCM of the numbers is 100.
Case - 3:
LCM of 8, 16, 19, 32

In this case only 8, 16 are divisors of 32 then eliminate 8, 16 from the list.19, 32
But 19 is prime then the LCM becomes
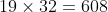
Then the LCM of the numbers is 608.
Example-1:
Find the LCM of the numbers 7, 14, 35, 70
Solution:
By Applying our case – 1 we can directly say the LCM is 70 as all the remaining numbers are divisors of highest number 70.
Example-2:
Find the LCM of the numbers 3, 9, 27, 63
Solution:
By Applying our case – 2 we can directly say the LCM is 189 as 9, 18 are divisors of highest number 72 and 189 is common least multiple of remaining numbers 27 and 63.
Therefore LCM = 189.
Example-3:
Find the LCM of the numbers 8, 11, 32, 64
Solution:
By Applying our case – 3 we can directly say the LCM is 704 as 8, 32 are divisors of highest number 64 and 11 is the prime number.
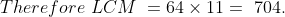
11 LCM and HCF - Trick #23
N/A
Finding HCF By Applying minimum difference method:
Case - 1:
HCF of 6, 12, 18
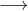 If the difference between the numbers are same then we need to consider the common difference.
If the difference between the numbers are same then we need to consider the common difference.
In this case the common difference is 6.
Note: If the common difference is a prime number then the HCF will be the prime number if that prime number is divisible by all of the given numbers else HCF will be ‘1’.
Else
 we need to prime factorize the difference.
we need to prime factorize the difference.
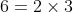
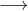 Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Divide 6, 12, 18 by 2 we get 3, 6, 9
Now divide 3, 6, 9 by 3 we get 1 2, 3
Therefore, qualified factors are 2, 3
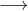 Now multiply the factors
Now multiply the factors
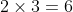
Therefore HCF = 6
Case - 2:
HCF of 12, 42, 66
 If the difference between the numbers are not same then we need to consider the minimum difference among them.
If the difference between the numbers are not same then we need to consider the minimum difference among them.
In this case
Difference from 12 to 42 = 30
Difference from 42 to 66 = 24
Difference from 12 to 66 = 54
Therefore, the minimum(least) difference is 24
Note: If the minimum difference is a prime number then the HCF will be the prime number if that prime number is divisible by all of the given numbers else HCF will be ‘1’.
Else
 Now we need to prime factorize the minimum difference.
Now we need to prime factorize the minimum difference.
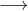 Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Divide 30, 24, 54 by 2 we get 15, 12, 18
Clearly remaining 2’s will not divide 15.
So now we need to check 3
Now divide 15, 12, 18 by 3 we get 5, 4, 6
Therefore, qualified factors are 2, 3
 Now multiply the factors
Now multiply the factors
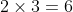
Therefore HCF = 6
Example-1:
Find the HCF of the numbers 7, 14, 21, 28
Solution:
By Applying our case – 1
The common difference is 7 and it is the prime number and divisible by all of the given numbers
Therefore HCF = 7
Example-2:
Find the HCF of the numbers 12, 30, 84, 102
Solution:
By Applying our case – 2
The minimum difference is 18 and it is not the prime number
Then prime factorization of 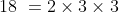
Divide 12, 30, 84, 102 by 2 we get 6, 15, 42, 51
Now divide 6, 15, 42, 51 by 3 we get 2, 5, 14, 17
But remaining 3 will not divide 2, 5, 14, 17
Then factors which are divisible by all of the given numbers are 2, 3
Example-3:
Find the HCF of the numbers 27, 32, 37, 42
Solution:
By Applying our case – 1
The common difference is 5 and it is the prime number but it is not divisible by all of the given numbers
Therefore HCF = 1
12 LCM and HCF - Trick #24
N/A
If we have LCM and HCF of two numbers then
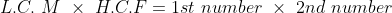
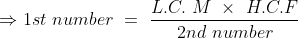
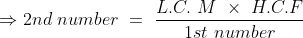
Example-1:
The LCM of two numbers is 864 and their HCF is 144. If one of the numbers are 288, the other number is?
Solution:
By Applying Trick 23,
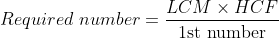


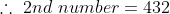
Example-2:
The product of two numbers is 1280 and their H.C.F. is 8. The L.C.M. of the numbers will be?
Solution:
By Applying Trick 23,
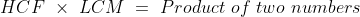
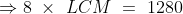
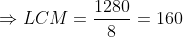
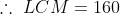
Example-3:
The product of two numbers is 4107 and their L.C.M. is 111. The H.C.F. of the numbers will be?
Solution:
By Applying Trick 23,
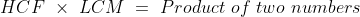

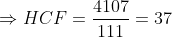
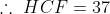
13 LCM and HCF - Trick #24
N/A
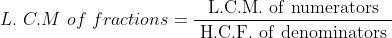
Example-1:
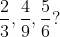
Solution:
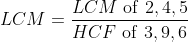
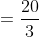
Example-2:
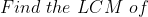
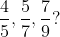
Solution:
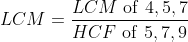

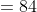
Example-3:
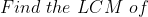
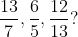
Solution:
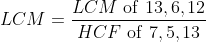
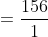
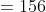
14 LCM and HCF - Trick #25
N/A
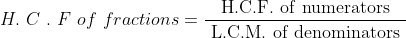
Example-1:
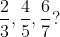
Solution:
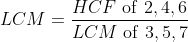
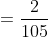
Example-2:
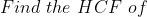
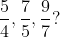
Solution:
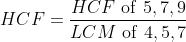

Example-3:
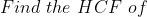
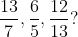
Solution:

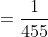
15 LCM and HCF - Trick #26
N/A
When a number is divided by a, b or c leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b and c.
Example-1:
The least number which when divided by 4, 6, 8, 12 and 16 leaves a remainder of 2 in each case is?
Solution:
By Applying Trick 26,
L.C.M. of 4, 6, 8, 12 and 16 = 48
 Required number = 48 + 2 = 50
Required number = 48 + 2 = 50
Example-2:
Find the least number which when divided separately by 15, 20, 36 and 48 leaves 3 as remainder in each case?
Solution:
By Applying Trick 26,
Required number = (LCM of 15, 20, 36 and 48) + 3
 LCM = 2 × 2 × 3 × 5 × 3 × 4 = 720
LCM = 2 × 2 × 3 × 5 × 3 × 4 = 720
 Required number = 720 + 3 = 723
Required number = 720 + 3 = 723
Example-3:
The least number, which when divided by 12, 15, 20 or 54 leaves a remainder of 4 in each case, is?
Solution:
By Applying Trick 26,
LCM of 15, 12, 20, 54 = 540
 Required number = 540 + 4 = 544
Required number = 540 + 4 = 544
16 LCM and HCF - Trick #27
N/A
When a number is divided by a, b or c leaving remainders p, q or r respectively such that the difference between divisor and remainder in each case is same i.e., (a – p) = (b – q) = (c – r) = t (say) then that (least) number must be in the form of (k – t), where k is LCM of a, b and c.
Example-1:
The least number, which when divided by 4, 5 and 6 leaves remainder 1, 2 and 3 respectively, is?
Solution:
By Applying Trick 27,
Here 4 – 1 = 3,
5 – 2 = 3,
6 – 3 = 3
 The required number = LCM of (4, 5, 6) – 3 = 60 – 3 = 57
The required number = LCM of (4, 5, 6) – 3 = 60 – 3 = 57
Example-2:
The smallest number, which when divided by 12 and 16 leaves remainder 5 and 9 respectively, is?
Solution:
By Applying Trick 27,
Here, 12 – 5 = 7,
16 – 9 = 7
 Required number = (L.C.M. of 12 and 16) – 7 = 48 – 7 = 41
Required number = (L.C.M. of 12 and 16) – 7 = 48 – 7 = 41
Example-3:
When a number is divided by 15, 20 or 35, each time the remainder is 8.
Then the smallest number is?
Solution:
LCM of 15, 20 and 35 = 420
 Required least number = 420 + 8 = 428
Required least number = 420 + 8 = 428
17 LCM and HCF - Trick #28
N/A
The largest number which when divide the numbers a, b and c the remainders are same then that largest number is given by H.C.F. of (a – b), (b – c) and (c – a).
Example:
The greatest number, which when divide 24, 30 and 48 leave same remainder is?
Solution:
,(30-48)&space;and&space;(48&space;-24))
= HCF of 6, 18 and 24
 HCF = 2
HCF = 2
18 LCM and HCF - Trick #29
N/A
The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by H.C.F. of (a – p), (b – q) and (c – r).
Example-1:
The greatest number, which when divide 989 and 1327 leave remainders 5 and 7 respectively, is?
Solution:
Required number = HCF of (989 – 5) and (1327 – 7)
= HCF of 984 and 1320 = 24
 HCF = 24
HCF = 24
Example-2:
What is the greatest number that will divide 307 and 330 leaving remainders 3 and 7 respectively?
Solution:
Required number = HCF of (307 – 3) and (330 – 7)
= HCF of 304 and 323 = 19
 HCF = 19
HCF = 19
Example-3:
Which greatest number will divide 3026 and 5053 leaving remainders 11 and 13 respectively?
Solution:
Required number = HCF of (3026 – 11) and (5053 – 13)
= HCF of 3015 and 5040 = 45
 HCF = 45
HCF = 45
19 LCM and HCF - Trick #30
N/A
Greatest n digit number which when divided by three numbers p, q, r leaves no remainder will be
Required Number = (n – digit greatest number) – R
R is the remainder obtained on dividing greatest n digit number by L.C.M of p, q, r.
Example-1:
The largest 4-digit number exactly divisible by each of 12, 15, 18 and 27 is?
Solution:
The largest number of 4-digits is 9999.
L.C.M. of divisors 12, 15, 18 and 27
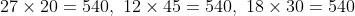
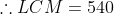
Divide 9999 by 540, now we get 279 as remainder. 9999 – 279 = 9720
Hence, 9720 is the largest 4-digit number exactly divisible by each of 12,
15, 18 and 27.
Example-2:
The greatest 4-digit number exactly divisible by 10, 15, 20 is?
Solution:
LCM of 10, 15 and 20 = 60
Largest 4-digit number = 9999
Divide 9999 by 60, now we get 39 as remainder. 9999 – 39 = 9960
Hence, 9960 is the largest 4-digit number exactly divisible by each of 10, 15 and 20.
20 LCM and HCF - Trick #31
N/A
The n digit largest number which when divided by p, q, r leaves remainder ‘a’ will be
Required number = [n – digit largest number – R] + a
where, R is the remainder obtained when n – digit largest number is divided by the L.C.M of p, q, r.
Example:
The largest number of five digits which, when divided by 16, 24, 30, or 36 leaves the same remainder 10 in each case, is?
Solution:
We will find the LCM of 16, 24, 30 and 36.
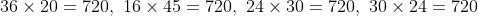
The largest number of five digits = 99999
On dividing 99999 by 720, the remainder = 639
 The largest five-digit number divisible by 720 = 99999 – 639 = 99360
The largest five-digit number divisible by 720 = 99999 – 639 = 99360
 Required number = 99360 + 10 = 99370
Required number = 99360 + 10 = 99370
21 Time and Distance - Trick #32
N/A
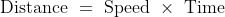
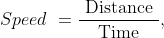
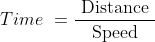
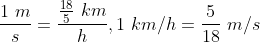
Example-1:
A train is travelling at the rate of 45km/hr. How many seconds it will take to cover a distance of 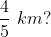
Solution:
By Applying Trick 32,
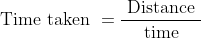
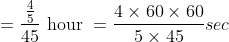

Example-2:
An aeroplane covers a certain distance at a speed of 240 km hour in 5 hours. To cover the same distance in 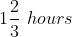 it must travel at a speed of?
it must travel at a speed of?
Solution:
By Applying Trick 32,
Let the required speed is x km/ hr
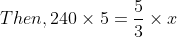
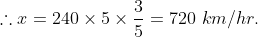
Example-3:
A man walking at the rate of 5 km/hr. crosses a bridge in 15 minutes. The length of the bridge (in metres) is?
Solution:
By Applying Trick 32,
Speed of the man = 5km/hr
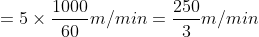
Time taken to cross the bridge
= 15 minutes Length of the bridge
= speed × time
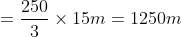
22 Time and Distance - Trick #33
N/A
If a man travels different distances 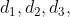 ....... and so on in different time
....... and so on in different time 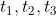 respectively then,
respectively then,
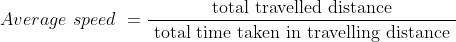
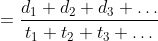
Example-1:
A man travels a distance of 24 km at 6 kmph. Another distance of 24 km at 8 kmph and a third distance of 24 km at 12 kmph. His average speed for the whole journey (in kmph) is?
Solution:
By Applying Trick 33,
Total distance = 24 + 24 + 24 = 72 km.
\mathrm{\&space;hours\&space;}=\&space;\left(4+3+2\right)\&space;hours=9\&space;hours\)
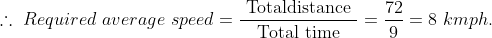
Example-2:
P travels for 6 hours at the rate of 5 km/hour and for 3 hours at the rate of 6 km/hour. The average speed of the journey in km/hour is?
Solution:
By Applying Trick 33,
Total distance = 5 × 6 + 3 × 6 = 30 + 18 = 48 km
Total time = 9 hours
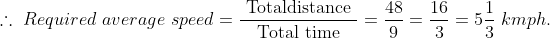
Example-3:
A train travelled at a speed of 35 km/hr for the first 10 minutes and at a speed of 20 km/hr for the next 5 minutes. The average speed of the train for the total 15 minutes is?
Solution:
By Applying Trick 33,
km\)
=\frac{45}{6}\mathrm{\&space;}km\)
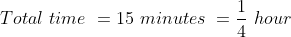
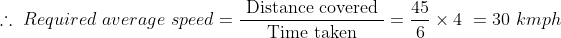
23 Time and Distance - Trick #34
N/A
If a man travels different distances 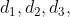 and so on with different speeds
and so on with different speeds 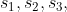 respectively then,
respectively then,
+\left(\frac{d_2}{s_2}\right)+\left(\frac{d_3}{s_3}\right)+\ldots})
Example:
A man travels a distance of 24 km at 6 kmph. Another distance of 24 km at 8 kmph and a third distance of 24 km at 12 kmph. His average speed for the whole journey (in kmph) is?
Solution:
By Applying Trick 34,
Total distance = 24 + 24 + 24 = 72 km.
\mathrm{\&space;hours\&space;}=\&space;\left(4+3+2\right)\&space;hours=9\&space;hours\)
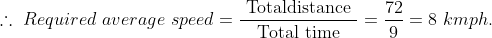
24 Time and Distance - Trick #35
N/A
If a distance is divided into “n” equal parts each travelled with different speeds, then,
})
where n = number of equal parts
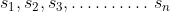 are speeds
are speeds
Example:
Four men travelled a distance which is divided into 4 equal parts with
speeds 5 kmph, 10 kmph, 15 kmph and 20 kmph then average speed?
Solution:
By Applying Trick 35,
Given that 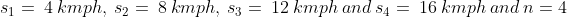
}\&space;=\frac{4}{\left(\frac{1}{5}+\frac{1}{10}+\frac{1}{15}+\frac{1}{20}\right)})
})
})
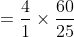
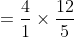
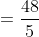
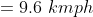
25 Time and Distance - Trick #36
N/A
If a bus travels from A to B with the speed x km/h and returns from B to A with the speed y km/h, then,
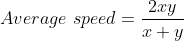
Example-1:
Jackson with his family travelled from Texas to New York by car at a speed of 40 km/hr and returned to Texas at a speed of 50 km/hr. The average speed for the whole journey is?
Solution:
By Applying Trick 36,
\&space;kmph)
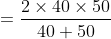
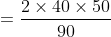
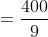
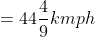
Example-2:
A boy goes to his school from his house at a speed of 3 km/hr and returns at a speed of 2 km/hr. If he takes 5 hours in going and coming, the distance between his house and school is?
Solution:
By Applying Trick 36,
Here, x = 3, y = 2
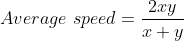
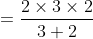
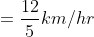
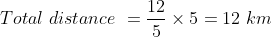

Example-3:
A boy goes to his school from his house at a speed of 3 km/hr and returns at a speed of 2 km/hr. If he takes 5 hours in going and coming, the distance between his house and school is?
Solution:
By Applying Trick 36,
Here, x = 25, y = 4
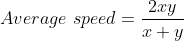
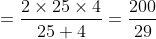

26 Time and Distance - Trick #37
N/A
If 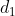 distance is travelled in
distance is travelled in 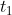 time and
time and 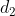 distance is travelled in
distance is travelled in 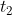 time then,
time then,

![\Rightarrow Distance\ \propto\ time\ [provided\ speed\ is\ constant]](https://latex.codecogs.com/gif.latex?\Rightarrow&space;Distance\&space;\propto\&space;time\&space;[provided\&space;speed\&space;is\&space;constant])
Example:
A man travelled 10 km in 2hrs and x km in 4hrs then find the value of x ?
Solution:
By Applying Trick 37,

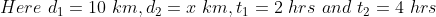
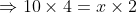
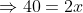
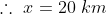
27 Time and Distance - Trick #38
N/A
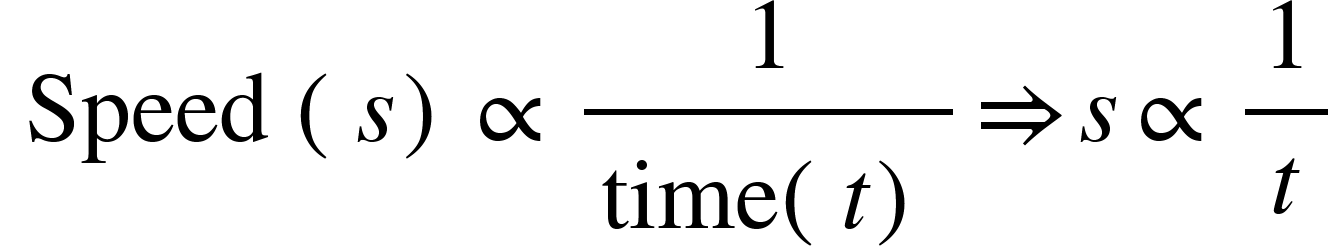
![\therefore{\ }s_1t_1=s_2t_2\ [provided\ distance\ is\ constant]](https://latex.codecogs.com/gif.latex?\therefore{\&space;}s_1t_1=s_2t_2\&space;[provided\&space;distance\&space;is\&space;constant])
Example:
A man travelled a distance of 24 km in 2hrs at what speed he needs to travel the same distance in 1.5 hrs?
Solution:
By Applying Trick 38,
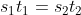
Here
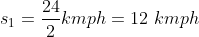
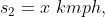
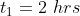
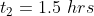
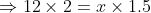
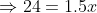
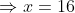
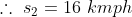
28 Time and Distance - Trick #39
N/A
If an object increases/decreases its speed from x km / hr to y km / hr to cover a distance in 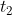 hours in place of
hours in place of 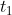 hours then
hours then
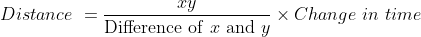
Or
\times&space;Change\&space;in\&space;time)
Example:
A Truck increases its speed from 45 kmph to 60 kmph in order to cover the distance in 6 hrs to deliver the goods 2 hrs earlier than expected time. Find the distance of the journey?
Solution:
By Applying Trick 39,
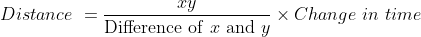
Or
)
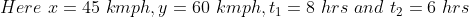
)


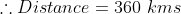
29 Time and Distance - Trick #40
N/A
If an object travels certain distance with the speed of A/B of its original speed and reaches its destination ‘t’ hours before or after, then the taken time by object travelling at original speed is
}\times\mathrm{\&space;time\&space;}(\mathrm{\&space;in\&space;hour\&space;}))
Example:
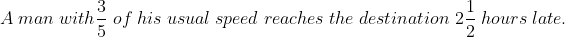
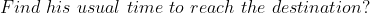
Solution:
By Applying Trick 40,
}\times\mathrm{\&space;time\&space;}(\mathrm{\&space;in\&space;hour\&space;}))
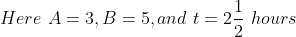
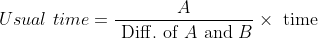
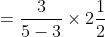
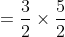
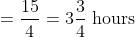
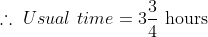
30 Time and Distance - Trick #41
N/A
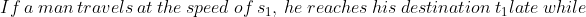
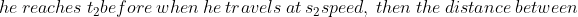
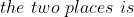
\times\left(t_1+t_2\right)}{s_2-s_1})
Example-1:
You arrive at your school 5 minutes late if you walk with a speed of 4 kmph,but you arrive 10 minutes before the scheduled time if you walk with a speed of 5 kmph. The distance of your school from your house (in km) is?
Solution:
By Applying Trick 41,
\left(t_1+t_2\right)}{s_2-s_1})
Here
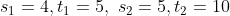
(5+10)}{5-4})
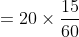
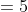

Example-2:
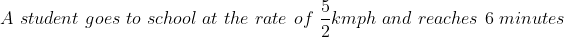
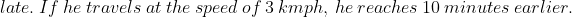

Solution:
By Applying Trick 41,
\left(t_1+t_2\right)}{s_2-s_1})
Here,
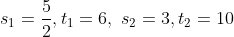
(6+10)}{3-\frac{5}{2}})
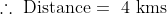
Example-3:

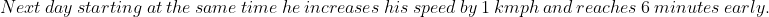
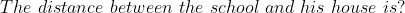
Solution:
By Applying Trick 41,
\left(t_1+t_2\right)}{s_2-s_1})
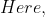
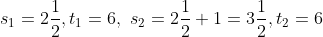
(6+6)}{\frac{7}{2}-\frac{5}{2}})

31 Time and Distance - Trick #42
N/A
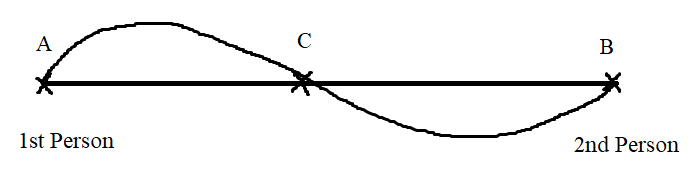
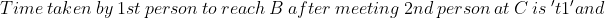

}{\mathrm{\&space;Speed\&space;of\&space;}2nd\&space;person\left(s_2\right)}=\sqrt{\frac{t_2}{t_1}})
Example-1:
Two trains X and Y start from City 1 to City 2 and from City 2 to City 1 respectively. After passing each other they take 4 hours 48 minutes and 3 hours 20 minutes to reach City 2 and City 1 respectively. If X is moving at 45 kmph, the speed of Y is?
Solution:
By Applying Trick 42,
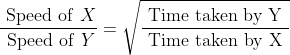
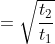
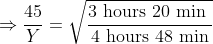

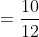
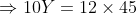
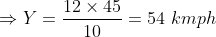
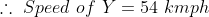
Example-2:
Two trains started at the same time, one from A to B and the other from B to A. If they arrived at B and A respectively 4 hours and 9 hours after they passed each other, the ratio of the speed of the two trains was?
Solution:
By Applying Trick 42,
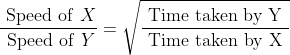
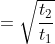

Example-3:
The distance between 2 places R and S is 42 km. Mike starts from R with a uniform speed of 4 kmph towards S and at the same time Jenny starts from S towards R also with some uniform speed. They meet each other after 6 hours. The speed of Jenny is?
Solution:
By Applying Trick 42,
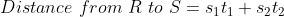
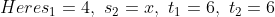


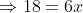
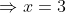
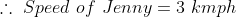
32 Time and Distance - Trick #43
N/A
If both objects run in opposite direction then,
Relative speed = Sum of speeds.
If both objects run in the same direction then,
Relative speed = Difference of Speeds.
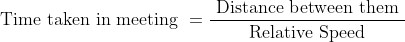
Example-1:

Solution:
By Applying Trick 43,
kmph=\frac{9}{2}\&space;kmph)
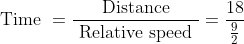
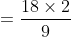

Example-2:
Motor-cyclist M started his journey at a speed of 30 kmph. After 30 minutes, motor-cyclist N started from the same place but with a speed of 40 kmph. How much time (in hours) will N take to overtake M?
Solution:
By Applying Trick 43,
Distance covered by motor cyclist M in 30 minutes
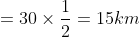
Relative speed = 40 – 30 = 10 kmph
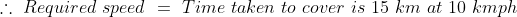
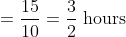
Example-3:
A thief is noticed by a policeman from a distance of 200m. The thief starts running and the policeman chases him. The thief and the policeman run at the rate of 10 kmph and 11 kmph respectively. What is the distance between them after 6 minutes?
Solution:
By Applying Trick 43,
Relative speed of police = 11 – 10 = 1 kmph
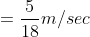
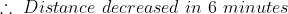
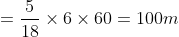
 Distance remained between them = 200–100 = 100 m
Distance remained between them = 200–100 = 100 m
33 Time and Distance - Trick #44
N/A
Let a man take ‘t’ hours to travel ‘x’ km. If he travels some distance on foot with the speed u km/h and remaining distance by cycle with the speed v km/h, then time taken to travel on foot.
}{(v-u)})
Distance travelled on foot = Time × u
Example-1:
A man travelled a distance of 80 km in 7 hrs partly on foot at the rate of 8 km per hour and partly on bicycle at 16km per hour. The distance travelled on the foot is
Solution:
By Applying Trick 44,
Here, x = 80, t = 7 u = 8, v = 16
)
)
)
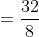
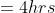
Distance travelled = 4 × 8 = 32 kms
Example-2:
A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot at the rate 4 kmph and partly on bicycle at the rate 9 kmph. The distance travelled on foot is?
Solution:
By Applying Trick 44,
Here, t = 9, x= 61, u = 4, v = 9
)
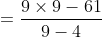

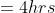
Distance travelled = 4 × 4 = 16 km
34 Time and Distance - Trick #45
N/A
If anyone overtakes or follows another, then
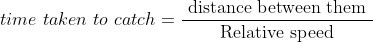
\times\mathrm{\&space;time\&space;}}{\mathrm{\&space;(Difference\&space;of\&space;speeds)\&space;}})
Total travelled distance to catch the thief
\times\mathrm{\&space;time\&space;}}{\mathrm{\&space;(Difference\&space;of\&space;speeds\&space;})})
Example:
A thief is noticed by a policeman from a distance of 500m. The thief starts running and the policeman chases him. The thief and the policeman run at the rate of 10 kmph and 11 kmph respectively. How many minutes will it take to policeman to catch the thief?
Solution:
By Applying Trick 45,
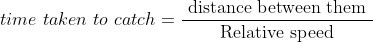
Relative speed = 11 – 10 = 1 kmph
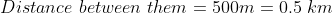
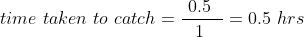
Therefore, time taken to catch the thief = 30 minutes
35 Time and Distance - Trick #46
N/A
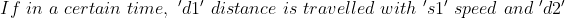
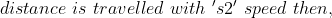
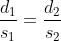
Example:
In a certain time, a man travelled 20 km at a speed of 2kmph. At what speed he needs to travel the distance of 25 km in the same time?
Solution:
By Applying Trick 46,
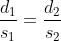
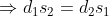
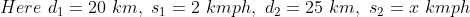
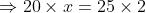
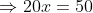

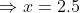
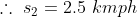
36 Time and Distance - Trick #47
N/A
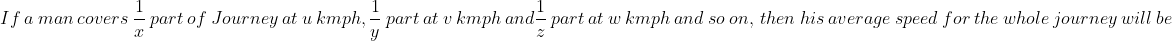

Example:
One third of a certain journey is covered at the rate of 25 kmph, one- fourth at the rate of 30 kmph and the rest at 50 kmph. The average speed for the whole journey is?
Solution:
By Applying Trick 47,
Here, x = 3, u = 25
y = 4, v = 30
z = 12/5, w = 50

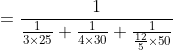
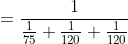
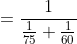
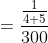
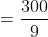
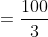
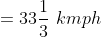
 Time taken in crossing ‘b’ metre length (i.e. platform, bridge, tunnel,standing train etc) by ‘a’ metre length train = total time taken in travelling(a + b) metre by the train.
Time taken in crossing ‘b’ metre length (i.e. platform, bridge, tunnel,standing train etc) by ‘a’ metre length train = total time taken in travelling(a + b) metre by the train.
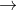 Let a train is travelling with the speed x kmph and in the same direction, another train is travelling on parallel path with the speed y kmph, then, Relative speed of the faster train = (x – y) kmph.
Let a train is travelling with the speed x kmph and in the same direction, another train is travelling on parallel path with the speed y kmph, then, Relative speed of the faster train = (x – y) kmph.
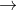 Suppose that a train is travelling with the speed ‘x’ kmph and from the opposite direction another train is coming on parallel path with the speed ‘y’ kmph, then Relative speed of the train = (x + y) kmph.
Suppose that a train is travelling with the speed ‘x’ kmph and from the opposite direction another train is coming on parallel path with the speed ‘y’ kmph, then Relative speed of the train = (x + y) kmph.
38 Trains - Trick #48
N/A
If a train crosses an electric pole, a sitting/ standing man, km or mile stone etc. then,
Distance = Length of train
Length of train = Speed × Time
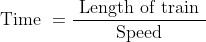
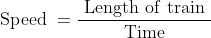
The length of a train and that of a platform are equal. If with a speed of 90 kmph the train crosses the platform in one minute, then the length of the train (in metres) is?
Solution:
By Applying Trick 48,
Let the length of train be x metre Speed = 90 kmph
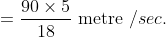
= 25 metre/sec
 Distance covered in 60 sec.
Distance covered in 60 sec.
= 25 × 60 = 1500 metres
Now, according to question,
2x = 1500
 x 750 metre
x 750 metre
39 Trains - Trick #49
N/A
Let ‘a’ metre long train is going with the speed ‘x’ m/s and ‘b’ metre long train is also going with the speed ‘y’ m/s in the same direction on parallel path, then total time taken by the faster train to cross the slower train
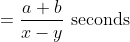
Here, a = 1800, b = 1600
x = = 15 m/s, y = 10 m/s
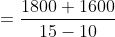
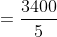
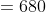
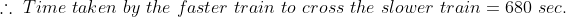
40 Trains - Trick #50
N/A
Let ‘a’ metre long train is going with the speed ‘x’ m/s and ‘b’ metre long train is also going with the speed ‘y’ m/s in the opposite direction on parallel path, then total time taken by the trains to cross each other

Example:
A 1200-metre-long train is going with the speed 22 m/s and 1500 metre long train is also going with the speed 28 m/s in the opposite direction on parallel path, then total time taken by the trains to cross each other?
Solution:
By Applying Trick 50,
Time taken by the trains to cross each other

Here, a = 1200, b = 1500
x = = 22 m/s, y = 28 m/s
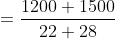
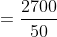
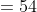
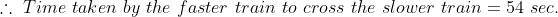
41 Trains - Trick #51
N/A
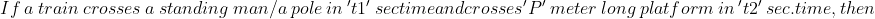
})
Example:
If a train crosses a standing pole in 15 sec time and crosses 120 meter long platform in 25 sec. time, then length of the train is?
Solution:
By Applying Trick 51,
})
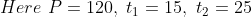
})

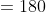
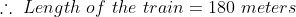
42 Trains - Trick #52
N/A
Let ‘a’ metre long train is running with the speed ‘x’ m/s. A man is running in same direction and with the speed ‘y’ m/s, then
}\&space;seconds)
Example:
A train 180 m long moving at the speed of 20 m/sec. over-takes a man moving at a speed of 10m/ sec in the same direction. The train passes the man in?
Solution:
By Applying Trick 52,
})
Here a = 180, x = 20, y = 10
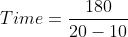
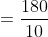
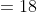
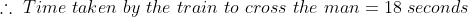
43 Trains - Trick #53
N/A
Let ‘a’ metre long train is running with the speed ‘x’ m/s. A man is running in opposite direction and with the speed ‘y’ m/s, then
}\&space;seconds)
Example:
A train, 240 m long crosses a man walking along the line in opposite direction at the rate of 3 kmph in 10 seconds. The speed of the train is?
Solution:
If the speed of train be x kmph then,
\&space;kmph)
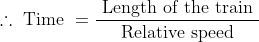
}=\frac{240}{1000(x+3)})
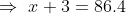

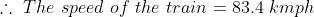
44 Trains - Trick #54
N/A
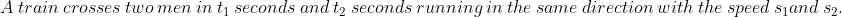

=\left(s_1-s_2\right)\left(\frac{t_1-t_2}{t_1-t_2}\right))
Example:
A train passes two persons walking in the same direction at a speed of 3 kmph and 5 kmph respectively in 10 seconds and 11 seconds respectively.
The speed of the train is?
Solution:
By Applying Trick 54,
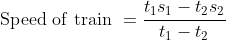
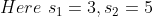
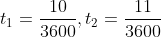

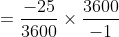

45 Trains - Trick #55
N/A
If two trains of (same lengths) are coming from same direction and cross a man in  seconds, then
seconds, then
Example:
If two trains A and B of same lengths are coming from same direction and cross a standing pole in 10 and 15 seconds, then time taken by both the trains to cross each other?
Solution:
By Applying Trick 55,
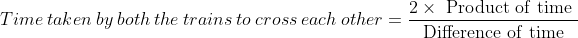
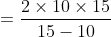
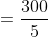
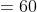
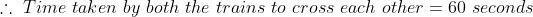
46 Trains - Trick #56
N/A
If two trains of (same lengths) are coming from opposite directions and cross a man in  seconds, then
seconds, then
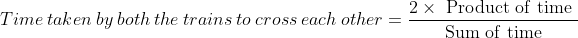
Example:
If two trains A and B of same lengths are coming from opposite directions and cross a standing pole in 20 and 30 seconds, then time taken by both the trains to cross each other?
Solution:
By Applying Trick 56,
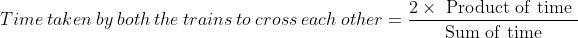
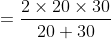
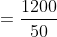
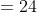
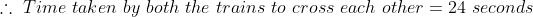
47 Trains - Trick #57
N/A
If a train of length x meters crosses a platform/ tunnel/bridge of length y meters with the speed u m/s in t seconds, then,
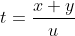
Example:
A train 300 metres long is running at a speed of 25 metres per second. It will cross a bridge of 200 metres in?
Solution:
By Applying Trick 57,

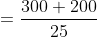
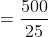
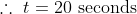
48 Trains - Trick #58
N/A
Two trains A and B, run from stations X to Y and from Y to X with the speed 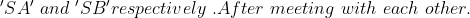
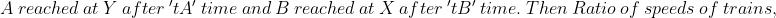
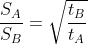
Example:
Two trains started at the same time, one from A to B and the other from B to A. If they arrived at B and A respectively 4 hours and 9 hours after they passed each other, the ratio of the speed of the two trains was?
Solution:
By Applying Trick 58,
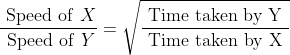
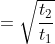

49 Trains - Trick #59
N/A
If a train of length l meters passes a bridge/ platform of 'x' meters in 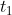 sec, then the time taken by the same train to cross another bridge/platform of length ‘y’ meters is,
sec, then the time taken by the same train to cross another bridge/platform of length ‘y’ meters is,
t_1)
Example:
If a train of length 800 meters passes a bridge of 200 meters in 8 sec, then the time taken by the same train to cross another bridge of length 250 meters is?
Solution:
By Applying Trick 59,
t_1)

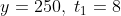
\times8)
\times8)
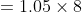

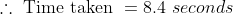
50 Trains - Trick #60
N/A
From stations A and B, two trains start travelling towards each other at speeds a and b, respectively. When they meet each other, it was found that one train covers distance d more than that of another train. The distance between stations A and B is given as
\times&space;d)
Example:
Two trains start from station A and B and travel towards each other at speed of 16 miles/ hour and 21 miles/ hour respectively. At the time of their meeting, the second train has travelled 60 miles more than the first.
The distance between A and B (in miles) is?
Solution:
By Applying Trick 60,
Here, a = 21, b = 16, d = 60
Distance between A and B
\times&space;d)
\times60)

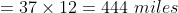
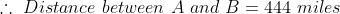
51 Trains - Trick #61
N/A
The distance between two places A and B is x km. A train starts from A towards B at a speed of ‘a’ km/ hr and after a gap of ‘t’ hours another train with speed ‘b’ km/hr starts from B towards A, then both the trains will meet at a certain point after time T. Then, we have.
)
t is taken as positive if second train starts after first train and t is taken as
negative if second train starts before the first train.
Example:
A train starts from City 1 towards City 2 at a speed of 40 kmph and after a
gap of 2 hours another train with speed 50 kmph starts from City 2
towards City 1, then after how many hours both the trains will meet if
the distance between two cities is 170 km?
Solution:
By Applying Trick 61,
)
Here second train starts after first train.
Here, x = 170, a = 40, b = 50, t = 2
}{40+50}\right))
)
= 3 hours.
52 Trains - Trick #62
N/A
A train covers a distance between stations A and B in time 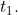 If the speed is changed by S. then the time taken to cover the same distance is
If the speed is changed by S. then the time taken to cover the same distance is  Then the distance (D) between A and B is given by
Then the distance (D) between A and B is given by
\mathrm{\&space;or\&space;}\left(\frac{S^\prime}{t^\prime}\right)t_1t_2)
Where t' : change in the time taken
Example:
A train covers a certain distance between stations P and Q in 4 hours. If the
speed is changed by 10 kmph, then the time taken to cover the same
distance is 3 hours. Then find the distance between P and Q?
Solution:
By Applying Trick 62,
)
Here, S = 10 kmph, 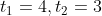
)
)
= 120
Therefore, distance between P and Q is 120 kms.
53 Ratio and Proportion - Formula
N/A
Ratio:
The comparative relation between two amounts/ quantities of same type is called ratio. The ratio of two amounts is equal to a fraction. It shows how much less or more time an amount is in comparison to another.
Ratio always occurs between same units, as –Dollars: Dollars, kg: kg, Hour: Hour, Second: Second etc.
Proportion:
When two ratios are equal to each other, then they are called proportional as 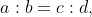 then, a, b, c and d are in proportion
then, a, b, c and d are in proportion
54 Ratio and Proportion - Trick #63
N/A
It does not change the ratio, when we multiply or divide antecedent and consequent of the ratio by a same non–zero number as
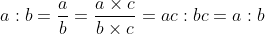
Where c is the non–zero number.
Example:
The ratio of two quantities is 2 to 3. If each of the two quantities is
tripled, what is the ratio of these two new quantities?
Solution:
By Applying Trick 63,
Tripling both quantities in a ratio (or multiplying each by any term, as a
matter of fact) doesn' t change the ratio. If you triple both terms
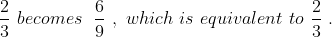
55 Ratio and Proportion - Trick #64
N/A
Mixed ratio:
Let x: y and P: Q be two ratios, then Px : Qy is called mixed ratio.
Example:
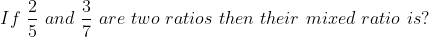
Solution:
By Applying Trick 64,
=\frac{6}{35})
56 Ratio and Proportion - Trick #65
N/A
Duplicate Ratio:
The mixed ratio of two equal ratios is called the duplicate Ratio as
duplicate ratio of a:b is 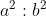
57 Ratio and Proportion - Trick #66
N/A
Sub-duplicate Ratio:
The square root of a certain ratio is called its sub-duplicate.
The sub-duplicate ratio of 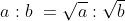
58 Ratio and Proportion - Trick #67
N/A
Triplicate Ratio:
The cube of a certain ratio is called triplicate ratio.
The triplicate ratio of 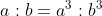
59 Ratio and Proportion - Trick #68
N/A
Sub-triplicate Ratio:
The cube root of a certain ratio is called sub-triplicate ratio as
The Sub-triplicate Ratio of ![a:b=\sqrt[3]{a}:\sqrt[3]{b}](https://latex.codecogs.com/gif.latex?a:b=\sqrt[3]{a}:\sqrt[3]{b})
60 Ratio and Proportion - Trick #69
N/A
Inverse Ratio:
The Reciprocal of quantities of ratio is called its inverse. Reciprocal or inverse ratio of a:b
\times\mathrm{\&space;(L.C.M.\&space;of\&space;}&space;a\mathrm{\&space;and\&space;}&space;b\right))
61 Ratio and Proportion - Trick #70
N/A
Invertendo:
The proportion in which antecedent and consequent quantities change their places, is called invertendo, as
Invertendo of 
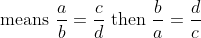
62 Ratio and Proportion - Trick #71
N/A
Alternendo:
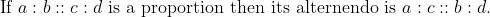
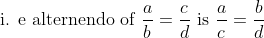
63 Ratio and Proportion - Trick #72
N/A
Componendo:
:&space;b::(c+d):&space;d)
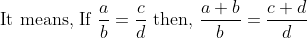
![\text { or, }\left[\frac{a}{b}+1=\frac{c}{d}+1 \Rightarrow \frac{a+b}{b}=\frac{c+d}{d}\right]](https://latex.codecogs.com/gif.latex?\text&space;{&space;or,&space;}\left[\frac{a}{b}+1=\frac{c}{d}+1&space;\Rightarrow&space;\frac{a+b}{b}=\frac{c+d}{d}\right])
64 Ratio and Proportion - Trick #73
N/A
:&space;b::(c-d):&space;d)
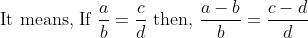
![\text { or, }\left[\frac{ a }{ b }-1=\frac{ c }{ d }-1 \Rightarrow \frac{ a - b }{ b }=\frac{ c - d }{ d }\right]](https://latex.codecogs.com/gif.latex?\text&space;{&space;or,&space;}\left[\frac{&space;a&space;}{&space;b&space;}-1=\frac{&space;c&space;}{&space;d&space;}-1&space;\Rightarrow&space;\frac{&space;a&space;-&space;b&space;}{&space;b&space;}=\frac{&space;c&space;-&space;d&space;}{&space;d&space;}\right])
65 Ratio and Proportion - Trick #74
N/A
Componendo and dividendo:
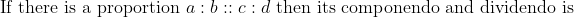
:(a-b)::(c+d):(c-d)&space;\text&space;{&space;or&space;}&space;\frac{a+b}{a-b}=\frac{c+d}{c-d})
To simplify the proportion any one method of componendo, dividendo, componendo and Dividendo can directly be used.
Example:
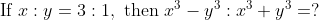
Solution:
By Applying Trick 74,

![\Rightarrow \frac{x^{3}-y^{3}}{x^{3}+y^{3}}=\frac{27-1}{27+1}\text { [By componendo and dividendo] }](https://latex.codecogs.com/gif.latex?\Rightarrow&space;\frac{x^{3}-y^{3}}{x^{3}+y^{3}}=\frac{27-1}{27+1}\text&space;{&space;[By&space;componendo&space;and&space;dividendo]&space;})
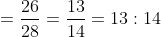
66 Ratio and Proportion - Trick #75
N/A
Mean Proportion:
Let x be the mean proportion between a and b, then 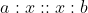 (Real condition)
(Real condition)
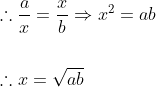
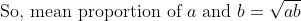
Example:
The mean proportional between &space;\text&space;{&space;and&space;}(12-\sqrt{32})&space;\text&space;{&space;is?&space;})
Solution:
By Applying Trick 75,
(12-\sqrt{32})}&space;\\&space;\\&space;&=\sqrt{(3+\sqrt{2})&space;4(3-\sqrt{2})}&space;\\&space;\\&space;&=2&space;\sqrt{9-2}&space;\\&space;\\&space;&=2&space;\sqrt{7}&space;\end{aligned})
67 Ratio and Proportion - Trick #76
N/A
Third proportional:
Let ‘x’ be the third proportional of a and b then,
)
)
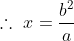
Example:
The third proportional of 12 and 18 is?
Solution:
By Applying Trick 76,

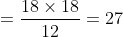
68 Ratio and Proportion - Trick #77
N/A
Fourth proportional:
Let ‘x’ be the fourth proportional of a, b and c then, )
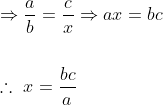
Example:
The fourth proportional to 0.12, 0.21, 8 is?
Solution:
By Applying Trick 77,
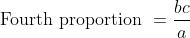
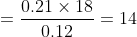
69 Ratio and Proportion - Trick #78
N/A
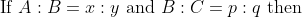
&space;}&space;A:&space;C=x&space;p:&space;y&space;q)
&space;}&space;A:&space;B:&space;C=(x:&space;y)&space;\times&space;p:&space;q&space;y=x&space;p:&space;y&space;p:&space;q&space;y)
It is done as follows:
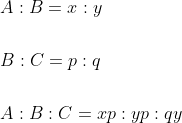
Example-1:
If a, b, c are three numbers such that a : b = 3 : 4 and b : c = 8 : 9, then a : c is equal to?
Solution:
By Applying Trick 78,
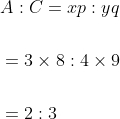
Example-2:
If A : B = 3 : 4 and B : C = 8 : 9, then A : B : C is?
Solution:
By Applying Trick 78,
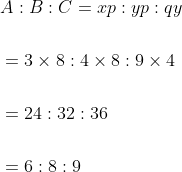
70 Ratio and Proportion - Trick #79
N/A
If A:B = x:y, B:C = p:q and C:D = m:n then,
&space;}&space;A:&space;D=x&space;p&space;m:&space;y&space;q&space;n)
&space;A:&space;B:&space;C:&space;D&space;}=(x&space;p:&space;y&space;p:&space;y&space;q)&space;\times&space;m:&space;y&space;q&space;n=x&space;p&space;m:&space;y&space;p&space;m:&space;y&space;q&space;m:&space;y&space;q&space;n)
Example-1:
If A : B = 3 : 4, B : C = 5 : 7 and C : D = 8 : 9 then A : D is equal to?
Solution:
By Applying Trick 79,

Example-2:
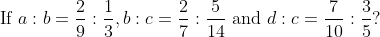
Solution:
By Applying Trick 79,
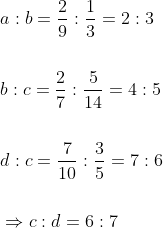
Thus,
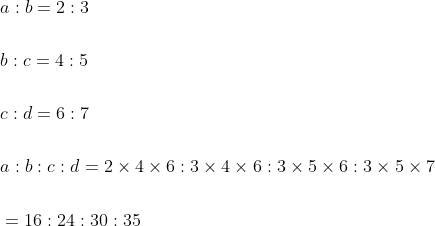
71 Ratio and Proportion - Trick #80
N/A
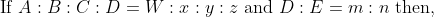
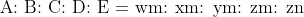
Example:
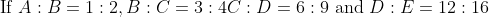
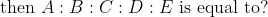
Solution:
By Applying Trick 80,
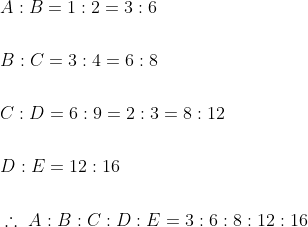
72 Ratio and Proportion - Trick #81
N/A
If an amount R is to be divided between A and B in the ratio m:n then
&space;Part&space;of&space;\(A=\frac{m}{m+n}&space;\times&space;R\))
&space;Part&space;of&space;\(B=\frac{n}{m+n}&space;\times&space;R\))
&space;Difference&space;of&space;part&space;of&space;}&space;A&space;\text&space;{&space;and&space;}&space;B=\frac{m&space;n}{m+n}&space;\times&space;R&space;\text&space;{,&space;})
where m > n
Example-1:
If an amount $250 is to be divided between P and Q in the ratio 3:2 then
how much will Q get on his part?
Solution:
By Applying Trick 81,

Therefore, Part of Q = 100
Example-2:
If $1000 is divided between A and B in the ratio 3 : 2, then A will receive?
Solution:
By Applying Trick 82,
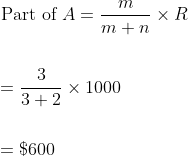
73 Ratio and Proportion - Trick #82
N/A
If the ratio of A and B is m:n and the difference in their share is ‘R’ units then,
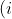&space;Part&space;of&space;\(A=\frac{m}{m-n}&space;\times&space;R\))
&space;Part&space;of&space;\(B&space;=\frac{&space;n&space;}{&space;m&space;-&space;n&space;}&space;\times&space;R\))
&space;The&space;sum&space;of&space;parts&space;of&space;\(A\)&space;and&space;\(B=\frac{m+n}{m-n}&space;\times&space;R\))
where m > n
Example:
If the ratio of A and B is 5:2 and the difference in their share is $75
then how much will A get?
Solution:
By Applying Trick 82,
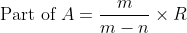
Here, m:n = 5:2 and R = 75,
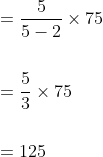
74 Ratio and Proportion - Trick #83
N/A
If the ratio of A and B is m:n and the part of A is ‘R’, then
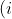\&space;Share&space;of&space;\(B=\frac{n}{m}&space;\times&space;R\))
\&space;Total&space;share&space;of&space;\(A\)&space;and&space;\(B=\frac{m+n}{m}&space;\times&space;R\))
&space;Difference&space;in&space;share&space;of&space;}&space;A&space;\text&space;{&space;and&space;}&space;B=\frac{m-n}{m}&space;\times&space;R)
where m > n
Example:
Marks of two candidates P and Q are in the ratio of 2 : 5. If the marks of P is
120, marks of Q will be?
Solution:
By Applying Trick 83,
&space;\\&space;\\&space;&=\frac{5}{2}&space;\times&space;120&space;\\&space;\\&space;&=300&space;\end{aligned})
75 Ratio and Proportion - Trick #84
N/A
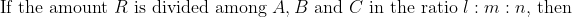
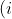\&space;The&space;share&space;of&space;\(A&space;=\frac{l}{l+&space;m&space;+&space;n&space;}&space;\times&space;R\))
\&space;The&space;share&space;of&space;\(B=\frac{m}{l+m+n}&space;\times&space;R\))
\&space;The&space;share&space;of&space;\(C=\frac{n}{l+m+n}&space;\times&space;R\))
\&space;Difference&space;in&space;share&space;of&space;\(A\)&space;and&space;\(B=\frac{l-m}{l+m+n}&space;\times&space;R\),)
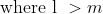
\&space;Difference&space;in&space;share&space;of&space;}&space;B&space;\text&space;{&space;and&space;}&space;C=\frac{l-n}{l+m+n}&space;\times&space;R)
where m>n
Example:
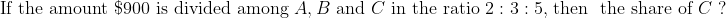
Solution:
By Applying Trick 84,
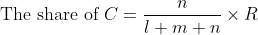
&space;})
76 Ratio and Proportion - Trick #85
N/A

\&space;Part&space;of&space;\(B=\frac{m}{l}&space;\times&space;R\))
\&space;Part&space;of&space;\(C=\frac{n}{l}&space;\times&space;R\))
\&space;Difference&space;in&space;parts&space;of&space;\(B\)&space;and&space;\(C=\frac{m-n}{l}&space;\times&space;R\))
\&space;where&space;\(m>n)\))
\&space;Total&space;share&space;of&space;\(A&space;,&space;B\)&space;and&space;\(C&space;=\frac{(l+&space;m&space;+&space;n&space;)}{l}&space;\times&space;R\))
77 Ratio and Proportion - Trick #86
N/A
If an amount is to be divided among A, B and C in the ratio l : m : n and the difference between A and B is ‘R’, then
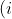\&space;Part&space;of&space;\(C=\frac{n}{l-m}&space;\times&space;R\),&space;where&space;\(l>&space;m\))
\&space;Total&space;share&space;of&space;\(A,&space;B\)&space;and&space;\(C=\frac{l+m+n}{l-m}&space;\times&space;R\)&space;where&space;\(l>m\))
&space;Difference&space;in&space;share&space;of&space;}&space;B&space;\text&space;{&space;and&space;}&space;C=\frac{m-n}{l-m}&space;\times&space;R,)
78 Ratio and Proportion - Trick #87
N/A
If there are notes of ‘x’ dollars, ‘y’ dollars and ‘z’ dollars in a box in the ratio m:n:r and the total value of notes is ‘R’, then
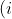\&space;Number&space;of&space;notes&space;of&space;\({&space;}^{\prime}&space;x&space;^{\prime}\)&space;dollars&space;\(=\frac{&space;m&space;}{(&space;xm&space;+&space;yn&space;+&space;zr&space;)}&space;\times&space;R\))
\&space;Number&space;of&space;notes&space;of&space;'&space;\(y&space;^{\prime}\)&space;dollars&space;\(=\frac{n}{(x&space;m+y&space;n+z&space;r)}&space;\times&space;R\))
\&space;Number&space;of&space;notes&space;of&space;\({&space;}^{\prime}&space;z&space;^{\prime}\)&space;dollars&space;\(=\frac{r}{(x&space;m+y&space;n+z&space;r)}&space;\times&space;R\))
79 Ratio and Proportion - Trick #88
N/A
If adding/subtracting a certain quantity gives new ratio, then multiplier
&space;}}{\text&space;{&space;Sum&space;of&space;Ratios&space;}})
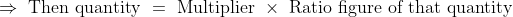
80 Ratio and Proportion - Trick #89
N/A
If the ratio of alligation of milk and water in a glass is m:n and in other glass alligation is p:q, then the ratio of milk and water in third glass which contains alligation of both glasses is
:\left(\frac{&space;n&space;}{&space;m&space;+&space;n&space;}+\frac{&space;q&space;}{&space;p&space;+&space;q&space;}\right))
81 Ratio and Proportion - Trick #90
N/A
If the ratio of milk and water in the alligation of A litre is p:q then water must be added in it so that ratio of milk and water would be r:s is
}{r(p+q)}&space;\text&space;{&space;litres&space;})
82 Ratio and Proportion - Trick #91
N/A
The ratio of income of two persons A and B is p:q. If the ratio of their expenditures are r:s, then the monthly income of A and B, when each one of them saves ‘R’ dollars will be
}{p&space;s-r&space;q}\))
}{p&space;s-r&space;q}\))
83 Ratio and Proportion - Trick #92
N/A
Let ‘x’ be a number which is subtracted from a, b, c and d to make them proportional, then
-(b+c)})
Let ‘x’ be a number which is added to a, b, c and d to make them proportional, then
-(b+c)})
Here, a, b, c and d should always be in ascending order.
Example-1:
When a particular number is subtracted from each of 7, 9, 11 and 15, the resulting numbers are in proportion. The number to be subtracted is?
Solution:
By Applying Trick 92,
The number will be x
-(b+c)}&space;\\&space;\\&space;&=\frac{7&space;\times&space;15-9&space;\times&space;11}{(7+15)-(9+11)}&space;\\&space;\\&space;&=\frac{105-99}{22-20}&space;\\&space;\\&space;&=\frac{6}{2}&space;\\&space;\\&space;&=3&space;\end{aligned})
Example-2:
Which number when added to each of the numbers 6, 7, 15, 17 will make the resulting numbers proportional?
Solution:
By Applying Trick 92,
Required number
-(b+c)})
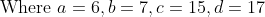
-(7+15)}&space;\\&space;\\&space;&=\frac{105-102}{23-22}&space;\\&space;\\&space;&=3&space;\end{aligned})
84 Ratio and Proportion - Trick #93
N/A
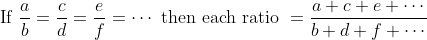
Example:
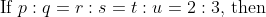
:(m&space;q+n&space;s+o&space;u)&space;\text&space;{&space;is&space;equal&space;to?&space;})
Solution:
By Applying Trick 93,

Here,
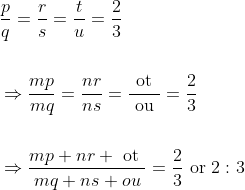
85 Ratio and Proportion - Trick #94
N/A
Two numbers are in the ratio a:b and if each number is increased by x, the ratio becomes c:d.
Then the two numbers will be
}{a&space;d-b&space;c}&space;\text&space;{&space;and&space;}&space;\frac{x&space;b(c-d)}{a&space;d-b&space;c})
Example:
If two numbers are in the ratio 2 : 3 and the ratio becomes 3 : 4 when 8 is
added to both the numbers, then the sum of the two numbers is?
Solution:
By Applying Trick 94,
Here, a = 2, b = 3, x= 8, c = 3, d = 4
}{a&space;d-b&space;c}&space;\\&space;\\&space;&=\frac{8&space;\times&space;2(3-4)}{2&space;\times&space;4-3&space;\times&space;3}&space;\\&space;\\&space;&=\frac{-16}{-1}=16&space;\end{aligned})
}{a&space;d-b&space;c}&space;\\&space;\\&space;&=\frac{8&space;\times&space;3(3-4)}{2&space;\times&space;4-3&space;\times&space;3}&space;\\&space;\\&space;&=\frac{-24}{-1}=24&space;\end{aligned})
Sum of numbers = 16 + 24 = 40
86 Ratio and Proportion - Trick #95
N/A
Two numbers are in the ratio a:b and if x is subtracted from each number the ratio becomes c:d.
The two numbers will be
}{a&space;d-b&space;c}&space;\text&space;{&space;and&space;}&space;\frac{x&space;b(d-c)}{a&space;d-b&space;c})
Example:
Two numbers are in the ratio 5 : 7. If 9 is subtracted from each of them, their ratio becomes 7 : 11. The difference of the numbers is?
Solution:
By Applying Trick 95,
Here, a = 5, b = 7, x = 9, c = 7, d = 11
}{a&space;d-b&space;c}&space;\\&space;\\&space;&=\frac{9&space;\times&space;5(11-7)}{5&space;\times&space;11-7&space;\times&space;7}&space;\\&space;\\&space;&=\frac{45&space;\times&space;4}{55-49}&space;\\&space;\\&space;&=\frac{45&space;\times&space;4}{6}&space;\\&space;\\&space;&=30&space;\end{aligned})
}{a&space;d-b&space;c}&space;\\&space;\\&space;&=\frac{9&space;\times&space;7(11-7)}{5&space;\times&space;11-7&space;\times&space;7}&space;\\&space;\\&space;&=\frac{63&space;\times&space;4}{55-49}&space;\\&space;\\&space;&=\frac{63&space;\times&space;4}{6}&space;\\&space;\\&space;&=42&space;\end{aligned})
If the ratio of present age and the ratio of age after ‘n’ years is given then present age factor is given by
&space;\times&space;\text&space;{&space;time&space;}}{(\text&space;{&space;Difference&space;in&space;cross&space;products&space;of&space;ratio&space;})})
If x is the present age factor, and the difference in cross product of ratio is zero then,
&space;}})
If the ratio of ‘some years ago’ and ‘after some years’ is given. And Before 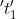 years, the ratio of ages of A and B was a : b.
years, the ratio of ages of A and B was a : b.
)
)
after 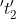 years, the ratio of their ages will be c: d.
years, the ratio of their ages will be c: d.
&space;\times\left(&space;t&space;_{1}+&space;t&space;_{2}\right)}{\text&space;{&space;(Difference&space;in&space;cross&space;products&space;of&space;the&space;ratio)&space;}})
When, the difference in ratios is equal, then
}{(\text&space;{&space;Difference&space;in&space;ratio&space;})})
If the product of present ages is given, then,
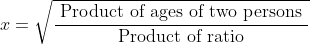
If sum of present age and ratio of the ages is given then, present age factor,

If the ratio of ages and difference in ages is given then,
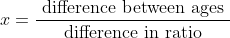
The ratio of ages of A and B was x: y ‘n’ years ago.
&space;If&space;the&space;present&space;age&space;ratio&space;is&space;a:&space;b,&space;then,&space;}&space;\frac{x+n}{y+n}=\frac{a}{b})
&space;If&space;after&space;'&space;}&space;m&space;^{\prime}&space;\text&space;{&space;years,&space;the&space;ratio&space;of&space;ages&space;will&space;be&space;})
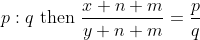
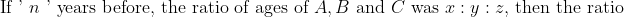
:(y+n):(z+n))
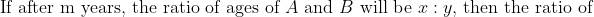

:(y-m))
96 Mixture or Alligation- Trick #105
N/A
The cost of cheap object is Rs. C/kg and the cost of costly object is Rs. D/kg.
If the mixture of both object costs Rs. M/kg. then

:(M-C))
97 Mixture or Alligation- Trick #106
N/A
Quantity of x in mixture
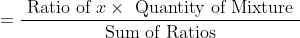
98 Mixture or Alligation- Trick #107
N/A
If from x litre of liquid A, p litre is withdrawn and same quantity of liquid B is added. Again, from mixture q litre mixture is withdrawn and same quantity of liquid B is added. Again, from mixture, r litre is withdrawn and same quantity of liquid B is added, then In final mixture, liquid A is
\left(\frac{x-q}{x}\right)\left(\frac{x-r}{x}\right)&space;\ldots&space;\ldots&space;\ldots)
If only one process is repeated n times, then liquid A in final mixture is
^{n}&space;\text&space;{&space;or&space;}&space;x\left(1-\frac{p}{x}\right)^{n})
&space;})
99 Mixture or Alligation- Trick #108
N/A
If x is initial amount of liquid, p is the amount which is drawn, and this process is repeated n-times such that the resultant mixture is in the ratio a: b then,
^{&space;n&space;})
100 Mixture or Alligation- Trick #109
N/A
There are two pots of same volume. Both the pots contain mixture of milk and water in the ratio m:n and p:q respectively. If both the mixtures are mixed together in a big pot, then what will be the final ratio of milk and water?
:\left(\frac{n}{m+n}+\frac{q}{p+q}\right))
101 Mixture or Alligation- Trick #110
N/A
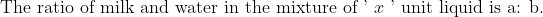
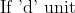
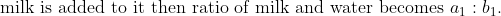
}{(a+b)&space;b_{1}}&space;\text&space;{&space;unit&space;})
If ‘d’ unit water is added to it then
}{(a+b)&space;a_{1}}&space;\text&space;{&space;unit&space;})
102 Mixture or Alligation- Trick #111
N/A
There is x% milk in ‘a’ unit mixture of milk and water.
The amount of milk that should be added to increase the percentage of milk from x% to y% is given by
}{(100-y)}&space;\text&space;{&space;unit.&space;})
103 Mixture or Alligation- Trick #112
N/A
There is x% water in ‘a’ unit the mixture of sugar and water.
The quantity of water vapourised such that decrease in the percentage of water is from x% to y% is given by
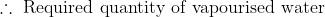
}{&space;y&space;}&space;\text&space;{&space;unit&space;})
104 Simple Interest : Formula
N/A
Principal or Sum:
The money borrowed or lent out for a certain period is called the principal or the sum.
Interest:
Extra money paid for using other’s money is called interest.
Simple Interest:
If the interest on a sum borrowed for a certain period is reckoned uniformly, then it is called simple interest.
Formulae:
Let Principal = P, Rate = R% per annum and time = T years.
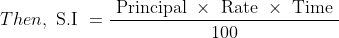
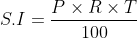
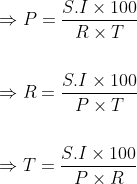
Example-1:
At some rate of simple interest, A lent $6000 to B for 2 years and $1500 to C for 4 years and received $900 as interest from both of them together. The rate of interest per annum was?
Solution:
If rate of interest be R% p.a. then,

Example-2:
$500 was invested at 12% per annum simple interest and a certain sum of money invested at 10% per annum simple interest. If the sum of the interest on both the sum after 4 years is $480, the latter sum of money is?
Solution:
Simple interest gained from $500

Let the other Principal be x.
S.I. gained = $(480 – 240) = $240
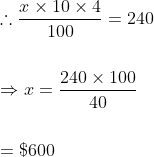
Example-3:
A lends $2500 to B and a certain sum to C at the same time at 7% annual simple interest. If after 4 years, A altogether receives $1120 as interest from B and C, the sum lent to C is?
Solution:
Let the sum lent to C be x According to the question,

or 2500 × 28 + 28x = 112000 or
2500 + x = 4000 or
x = 4000 – 2500 = 1500
105 Simple Interest - Trick #113
N/A
If there are distinct rates of interest for distinct time periods i.e.
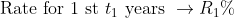
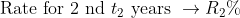
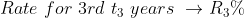
}{100})
106 Simple Interest - Trick #114
N/A
If a certain sum becomes ‘n’ times of itself in T years on Simple Interest, then the rate per cent per annum is.
}{&space;T&space;}&space;\times&space;100&space;\%\)&space;and)
}{&space;R&space;}&space;\times&space;100&space;\%)
Example-1:
A sum of money becomes 7/6 of itself in 3 years at a certain rate of simple interest. The rate per annum is?
Solution:
By Applying Trick 114,
&space;\times&space;100&space;\%}{3}&space;\\&space;\\&space;&=\frac{1}{18}&space;\times&space;100&space;\%&space;\\&space;\\&space;&=\frac{50}{9}&space;\%&space;\\&space;\\&space;&=5&space;\frac{5}{9}&space;\%&space;\end{aligned})
Example-2:
In how many years will a sum of money double itself at 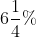 simple interest per annum?
simple interest per annum?
Solution:
By Applying Trick 114,
}{&space;R&space;\%}&space;\text&space;{&space;years&space;}&space;\\&space;\\&space;&=\frac{(2-1)}{\frac{25}{4}}&space;\times&space;100&space;\text&space;{&space;years&space;}&space;\\&space;\\&space;&=16&space;\text&space;{&space;years&space;}&space;\end{aligned})
107 Simple Interest - Trick #115
N/A
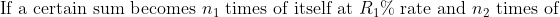
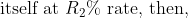
}{\left(&space;n&space;_{1}-1\right)}&space;R&space;_{1}&space;\text&space;{&space;and&space;}&space;T&space;_{2}=\frac{\left(&space;n&space;_{2}-1\right)}{\left(&space;n&space;_{1}-1\right)}&space;T&space;_{1})
108 Simple Interest - Trick #116
N/A
If Simple Interest (S.I.) becomes ‘n’ times of principal i.e.
S.I. = P × n then.
RT = n × 100
Example-1:
The simple interest on a sum after 4 years is 1/5 of the sum. The rate of interest per annum is?
Solution:
By Applying Trick 116,
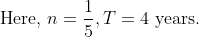
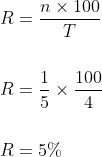
Example-2:
Simple interest on a certain sum for 6 years is 9/25 of the sum. The rate of interest is?
Solution:
By Applying Trick 116,
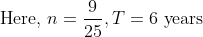
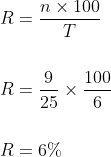
109 Simple Interest - Trick #117
N/A
If an Amount (A) becomes ‘n’ times of certain sum (P) i.e.
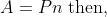
&space;\times&space;100)
110 Simple Interest - Trick #118
N/A
If the difference between two simple interests is ‘x’ calculated at different annual rates and times, then principal (P) is
&space;\times(\text&space;{&space;difference&space;in&space;time&space;})})
Example:
The difference between the simple interest received from two different
banks on $500 for 2 years is $2.50. The difference between their (per
annum) rate of interest is?
Solution:
By Applying Trick 118,
Here, P = $500, x = $2.50, Difference in time = 2 years.
Difference in rate =?
&space;\times&space;2})
Different in rate = 0.25%
111 Simple Interest - Trick #119
N/A
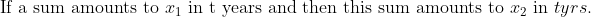

&space;\times&space;100}{(\text&space;{&space;Change&space;in&space;interest&space;Rate&space;})&space;\times&space;\text&space;{&space;time&space;}})
112 Simple Interest - Trick #120
N/A
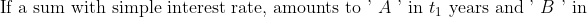
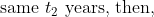
&space;\times&space;100}{A&space;\cdot&space;t_{2}-B&space;\cdot&space;t_{1}})
and
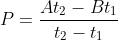
113 Simple Interest - Trick #121
N/A
If a sum is to be deposited in equal instalments, then,
![\text { Equal installment }=\frac{ A \times 200}{ T [200+( T -1) r ]}](https://latex.codecogs.com/gif.latex?\text&space;{&space;Equal&space;installment&space;}=\frac{&space;A&space;\times&space;200}{&space;T&space;[200+(&space;T&space;-1)&space;r&space;]})
Example-1:
What annual instalment will discharge a debt of $6450 due in 4 years at 5% simple interest?
Solution:
By Applying Trick 121,
![\begin{aligned} &=\frac{6450 \times 200}{4[200+(4-1) \times 5]} \\ \\ &=\frac{6450 \times 200}{4(215)} \\ \\ &=\frac{6450 \times 50}{215} \\ \\ &=\$ 1500 \end{aligned}](https://latex.codecogs.com/gif.latex?\begin{aligned}&space;&=\frac{6450&space;\times&space;200}{4[200+(4-1)&space;\times&space;5]}&space;\\&space;\\&space;&=\frac{6450&space;\times&space;200}{4(215)}&space;\\&space;\\&space;&=\frac{6450&space;\times&space;50}{215}&space;\\&space;\\&space;&=\$&space;1500&space;\end{aligned})
Example-2:
What equal instalment of annual payment will discharge a debt which is due as $848 at the end of 4 years at 4% per annum simple interest?
Solution:
By Applying Trick 121,
Here, A = $848, T = 4 years, r = 4%
![\begin{aligned} &=\frac{848 \times 200}{4[200+(4-1) 4]} \\ \\ &=\frac{848 \times 200}{4 \times 212} \\ \\ &=\$ 200 \end{aligned}](https://latex.codecogs.com/gif.latex?\begin{aligned}&space;&=\frac{848&space;\times&space;200}{4[200+(4-1)&space;4]}&space;\\&space;\\&space;&=\frac{848&space;\times&space;200}{4&space;\times&space;212}&space;\\&space;\\&space;&=\$&space;200&space;\end{aligned})
114 Simple Interest - Trick #122
N/A
To find the rate of interest under current deposit plan,
&space;\times(\text&space;{&space;deposited&space;amount&space;})})
where n = no. of months
115 Simple Interest - Trick #124
N/A

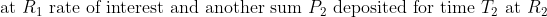
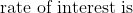
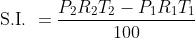
Example-1:
The simple interest on a certain sum at 5% per annum for 3 years and 4
years differ by $42. The sum is?
Solution:
By Applying Trick 124,
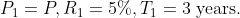
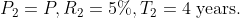
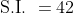

Example-2:
The difference between the simple interest received from two different sources on $1500 for 3 years is 413.50. The difference between their rates of interest is?
Solution:
By Applying Trick 124
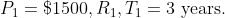
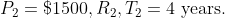
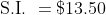
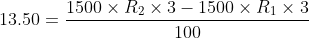
}{100})
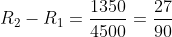
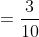
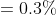
116 Simple Interest - Trick #123
N/A
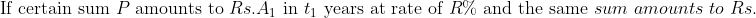
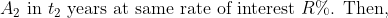
&space;}&space;R=\left(\frac{A_{1}-A_{2}}{A_{2}&space;T_{1}-A_{1}&space;T_{2}}\right)&space;\times&space;100)
&space;}&space;P=\left(\frac{A_{2}&space;T&space;_{1}-A_{1}&space;T&space;_{2}}{&space;T&space;_{1}-&space;T&space;_{2}}\right))
Example:
A sum of money lent at simple interest amounts to $880 in 2 years and to $920 in 3 years. The sum of money (in dollars) is?
Solution:
&space;\\&space;\\&space;&=\left(\frac{920&space;\times&space;2-880&space;\times&space;3}{2-3}\right)&space;\\&space;\\&space;&=\left(\frac{1840-2640}{-1}\right)&space;\\&space;\\&space;&=\frac{-800}{-1}&space;\\&space;\\&space;&=\$&space;800&space;\end{aligned})
117 Compound Interest : Formula
N/A
Sometimes it so happens that the borrower and the lender agree to fix up a certain unit of time, say yearly or half yearly or quarterly to settle the previous account. In such case, the amount after first unit of time becomes the principal for the second unit, the amount after second unit becomes the principal for the third unit and so on. After a specified period, the difference between the amount and the money borrowed is called the Compound Interest (abbreviated as C.I.) for that period.
Let Principal = P, Rate = R% per annum, Time = n years.
^{&space;n&space;})
![\text { When interest is compounded Half - yearly: Amount }= P \left[1+\frac{( R / 2)}{100}\right]^{2 n }](https://latex.codecogs.com/gif.latex?\text&space;{&space;When&space;interest&space;is&space;compounded&space;Half&space;-&space;yearly:&space;Amount&space;}=&space;P&space;\left[1+\frac{(&space;R&space;/&space;2)}{100}\right]^{2&space;n&space;})
![\text { When interest is compounded Quarterly: Amount }= P \left[1+\frac{( R / 4)}{100}\right]^{4 n }](https://latex.codecogs.com/gif.latex?\text&space;{&space;When&space;interest&space;is&space;compounded&space;Quarterly:&space;Amount&space;}=&space;P&space;\left[1+\frac{(&space;R&space;/&space;4)}{100}\right]^{4&space;n&space;})

^{3}&space;\times\left(1+\frac{\frac{2}{5}&space;R}{100}\right))
Example-1:
The compound interest on $10,000 in 2 years at 4% per annum, the interest being compounded half-yearly, is?
Solution:
^{4}&space;\\&space;\\&space;&=10,000\left(\frac{51}{50}\right)^{4}=10824.3216&space;\end{aligned})
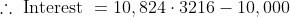
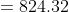
Example-2:
In what time will 1000 becomes 1331 at 10% per annum compounded annually?
Solution:
Let the required time be n years. Then,
![\begin{aligned} &1331=1000\left(1+\frac{10}{100}\right)^{ n } \\ \\ &{\left[\therefore P _{1}= P \left(1+\frac{ r }{100}\right)^{ n }\right]} \\ \\ &\Rightarrow \frac{1331}{1000}=\left(\frac{10+1}{10}\right)^{ n } \\ \\ &\Rightarrow\left(\frac{11}{10}\right)^{ n }=\left(\frac{11}{10}\right)^{3} \\ \\ &\Rightarrow n =3 \end{aligned}](https://latex.codecogs.com/gif.latex?\begin{aligned}&space;&1331=1000\left(1+\frac{10}{100}\right)^{&space;n&space;}&space;\\&space;\\&space;&{\left[\therefore&space;P&space;_{1}=&space;P&space;\left(1+\frac{&space;r&space;}{100}\right)^{&space;n&space;}\right]}&space;\\&space;\\&space;&\Rightarrow&space;\frac{1331}{1000}=\left(\frac{10+1}{10}\right)^{&space;n&space;}&space;\\&space;\\&space;&\Rightarrow\left(\frac{11}{10}\right)^{&space;n&space;}=\left(\frac{11}{10}\right)^{3}&space;\\&space;\\&space;&\Rightarrow&space;n&space;=3&space;\end{aligned})
Example-3:
The principal, which will amount to $270.40 in 2 years at the rate of 4% per annum compound interest, is?
Solution:
Let the principal be $P
^{2}&space;\\&space;\\&space;&\Rightarrow&space;270.40=&space;P&space;(1+0.04)^{2}&space;\\&space;\\&space;&\Rightarrow&space;P&space;=\frac{270.40}{1.04&space;\times&space;1.04}&space;\\&space;\\&space;&=\$&space;250&space;\end{aligned})
118 Compound Interest - Trick #125
N/A
If there are distinct ‘rates of interest’ for distinct time periods i.e.,
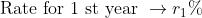

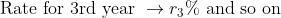
\left(1+\frac{&space;r&space;_{2}}{100}\right)\left(1+\frac{&space;r&space;_{3}}{100}\right))
C.I. = A – P
Example:
If the rate of interest be 4% per annum for first year, 5% per annum for second year and 6% per annum for third year, then the compound interest of $10,000 for 3 years will be?
Solution:
By Applying Trick 125,
\left(1+\frac{R_{2}}{100}\right)\left(1+\frac{R_{3}}{100}\right)&space;\\&space;\\&space;&=10000\left(1+\frac{4}{100}\right)\left(1+\frac{5}{100}\right)\left(1+\frac{6}{100}\right)&space;\\&space;\\&space;&=10000&space;\times&space;\frac{26}{25}&space;\times&space;\frac{21}{20}&space;\times&space;\frac{53}{50}&space;\end{aligned})
A = $11575.2
C.I. = $(11575.2–10000)
= $1575.2
119 Compound Interest - Trick #126
N/A
If the time is in fractional form i.e., t = nF, then
^{n}\left(1+\frac{r&space;F}{100}\right)&space;\text&space;{&space;e.g.t&space;}=3&space;\frac{5}{7}&space;y&space;r&space;s&space;\text&space;{,&space;then&space;})
^{3}\left(1+\frac{r}{100}&space;\times&space;\frac{5}{7}\right))
Example:
Find compound interest on 10,000 for 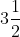 years at 10% per annum, compounded yearly?
years at 10% per annum, compounded yearly?
Solution:
By Applying Trick 126,
^{3}\left(1+\frac{\frac{r}{2}}{100}\right)&space;\\&space;\\&space;&=10,000\left(1+\frac{10}{100}\right)^{3}\left(1+\frac{5}{100}\right)&space;\\&space;\\&space;&=10,000&space;\times&space;\frac{1331}{1000}&space;\times&space;\frac{21}{20}&space;\end{aligned})
A = $13975.5
CI = $(13975.5 – 10,000)
CI = $3975.5
120 Compound Interest - Trick #127
N/A
A certain sum becomes ‘m’ times of itself in ‘t’ years on compound interest then the time it will take to become mn times of itself is t × n years.
Example:
A sum of money placed at compound interest doubles itself in 5 years. In how many years, it would amount to eight times of itself at the same rate of interest?
Solution:
By Applying Trick 127,
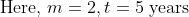
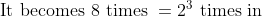
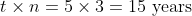
121 Compound Interest - Trick #128
N/A
The difference between C.I. and S.I. on a sum ‘P’ in 2 years at the rate of R% rate of compound interest will be
^{2}=\frac{\text&space;{&space;S.I.&space;}&space;\times&space;R&space;}{200})
^{2}&space;\times\left(3+\frac{R}{100}\right))
Example:
If the difference between the compound interest and simple interest on a sum at 5% rate of interest per annum for three years is 36.60, then the sum is?
Solution:
By Applying Trick 128,
^{2}&space;\times\left(3+\frac{R}{100}\right)&space;\\&space;\\&space;&36.60=P\left(\frac{5}{100}\right)^{2}&space;\times\left(3+\frac{5}{100}\right)&space;\\&space;\\&space;&36.60=P&space;\times&space;\frac{25}{100^{2}}&space;\times&space;\frac{305}{100}&space;\\&space;\\&space;&P=\frac{36.60&space;\times&space;100&space;\times&space;100&space;\times&space;100}{25&space;\times&space;305}&space;\\&space;\\&space;&P=\frac{36600000}{25&space;\times&space;305}=\$&space;4800&space;\end{aligned})
122 Compound Interest - Trick #129
N/A
If on compound interest, a sum becomes A in ‘a’ years and B in ‘b’ years then,
&space;If&space;}&space;b&space;-&space;a&space;=1&space;\text&space;{,&space;then,&space;}&space;R&space;\%=\left(\frac{&space;B&space;}{&space;A&space;}-1\right)&space;\times&space;100&space;\%)
&space;If&space;}&space;b-a=2&space;\text&space;{,&space;then,&space;}&space;R&space;\%=\left(\sqrt{\frac{B}{A}}-1\right)&space;\times&space;100&space;\%)
![\text { (iii) If } b-a=n \text { then, } R \%=\left[\left(\frac{B}{A}\right)^{\frac{1}{n}}-1\right] \times 100 \%](https://latex.codecogs.com/gif.latex?\text&space;{&space;(iii)&space;If&space;}&space;b-a=n&space;\text&space;{&space;then,&space;}&space;R&space;\%=\left[\left(\frac{B}{A}\right)^{\frac{1}{n}}-1\right]&space;\times&space;100&space;\%)
where n is a whole number
Example:
A sum of money amounts to $4,840 in 2 years and to $5,324 in 3 years at compound interest compounded annually. The rate of interest per annum is?
Solution:
By Applying Trick 129,
Here, b – a = 3 – 2 = 1 B = $5,324, A = $4,840
&space;\times&space;100&space;\%&space;\\&space;\\&space;&=\left(\frac{5324}{4840}-1\right)&space;\times&space;100&space;\%&space;\\&space;\\&space;&=\left(\frac{5324-4840}{4840}\right)&space;\times&space;100&space;\%&space;\\&space;\\&space;&=\frac{484}{4840}&space;\times&space;100&space;\%&space;\\&space;\\&space;&=10&space;\%&space;\end{aligned})
123 Compound Interest - Trick #130
N/A
If a sum becomes ‘n’ times of itself in ‘t’ years on compound interest, then
![R \%=\left[ n ^{\frac{1}{ t }}-1\right] \times 100 \%](https://latex.codecogs.com/gif.latex?R&space;\%=\left[&space;n&space;^{\frac{1}{&space;t&space;}}-1\right]&space;\times&space;100&space;\%)
Example:
If the amount is 2.25 times of the sum after 2 years at compound interest (compound annually), the rate of interest per annum is?
Solution:
By Applying Trick 130,
Here, n = 2.25, t = 2 years
![\begin{aligned} & R \%=\left( n ^{\frac{1}{t}}-1\right) \times 100 \% \\ \\ & R \%=\left[(2.25)^{\frac{1}{2}}-1\right] \times 100 \% \\ \\ &=[1.5-1] \times 100 \% \\ \\ &=0.5 \times 100 \% \\ \\ &=50 \% \end{aligned}](https://latex.codecogs.com/gif.latex?\begin{aligned}&space;&&space;R&space;\%=\left(&space;n&space;^{\frac{1}{t}}-1\right)&space;\times&space;100&space;\%&space;\\&space;\\&space;&&space;R&space;\%=\left[(2.25)^{\frac{1}{2}}-1\right]&space;\times&space;100&space;\%&space;\\&space;\\&space;&=[1.5-1]&space;\times&space;100&space;\%&space;\\&space;\\&space;&=0.5&space;\times&space;100&space;\%&space;\\&space;\\&space;&=50&space;\%&space;\end{aligned})
124 Compound Interest - Trick #131
N/A
If a sum ‘P’ is borrowed at r% annual compound interest which is to be paid in ‘n’ equal annual installments including interest, then
&space;for&space;}&space;n=2&space;\text&space;{,&space;Each&space;annual&space;installment&space;})
+\left(\frac{100}{100+r}\right)^{2}})
&space;For&space;}&space;n=3&space;\text&space;{,&space;Each&space;annual&space;instalment&space;})
+\left(\frac{100}{100+r}\right)^{2}+\left(\frac{100}{100+r}\right)^{3}})
Example:
A builder borrows $2550 to be paid back with compound interest at the rate of 4% per annum by the end of 2 years in two equal yearly instalments.
How much will each instalment be?
Solution:
By Applying Trick 131,
Here, P = $2550, n = 2, r = 4%
+\left(\frac{100}{100+&space;r&space;}\right)^{2}}&space;\\&space;\\&space;&=\frac{2550}{\left(\frac{100}{100+4}\right)+\left(\frac{100}{100+4}\right)^{2}}&space;\\&space;\\&space;&=\frac{2550}{\frac{100}{104}+\left(\frac{100}{104}\right)^{2}}&space;\\&space;\\&space;&=\frac{2550}{\frac{100}{104}\left(1+\frac{100}{104}\right)}&space;\\&space;\\&space;&=\frac{2550}{\frac{100}{104}\left(\frac{204}{104}\right)}&space;\\&space;\\&space;&=\frac{2550&space;\times&space;104&space;\times&space;104}{20400}&space;\\&space;\\&space;&=\$&space;1352&space;\end{aligned})
125 Compound Interest - Trick #132
N/A
The simple interest for a certain sum for 2 years at an annual rate interest R% is S.I., then
)
Example:
If the compound interest on a sum for 2 years at 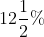 per annum is $510, the simple interest on the same sum at the same rate for the same period of time is?
per annum is $510, the simple interest on the same sum at the same rate for the same period of time is?
Solution:
By Applying Trick 132,
Here, C.I. = $510
&space;\\&space;\\&space;&510=\text&space;{&space;S.I.&space;}\left(1+\frac{25}{400}\right)&space;\\&space;\\&space;&\text&space;{&space;S.I.&space;}=\frac{510&space;\times&space;400}{425}&space;\\&space;\\&space;&\text&space;{&space;S.I.&space;}=\$&space;480&space;\end{aligned})
126 Compound Interest - Trick #133
N/A

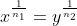
Example-1:
A sum of $12,000, deposited at compound interest becomes double after 5 years. How much will it be after 20 years?
Solution:
By Applying Trick 133,
^{20}&space;\\&space;\\&space;&y=2^{4}&space;\\&space;\\&space;&y=16&space;\text&space;{&space;times&space;}&space;\end{aligned})
Example-2:
A sum of money becomes double in 3 years at compound interest compounded annually. At the same rate, in how many years will it become four times of itself?
Solution:
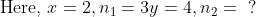
^{\frac{1}{n_{2}}}&space;\\&space;\\&space;&\Rightarrow&space;2^{\frac{1}{3}}=2^{\frac{2}{n_{2}}}&space;\\&space;\\&space;&\frac{1}{3}=\frac{2}{n_{2}}&space;\\&space;\\&space;&\therefore&space;n_{2}=6&space;\text&space;{&space;years&space;}&space;\end{aligned})
Example-3:
A sum of money placed at compound interest doubles itself in 4 years. In how many years will it amount to four times itself?
Solution:

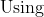
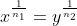
^{\frac{1}{4}}=(4)^{\frac{1}{&space;n&space;_{2}}}\))
^{\frac{1}{4}}=\left(2^{2}\right)^{\frac{1}{n_{2}}}\))
^{\frac{1}{4}}=(2)^{\frac{2}{n_{2}}}\))

127 Time and Work - Formula
N/A
Work Word Problem:
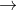 It involves a number of people or machines working together to complete a task.
It involves a number of people or machines working together to complete a task.
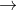 We are usually given individual rates of completion.
We are usually given individual rates of completion.
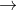 We are asked to find out how long it would take if they work together.
We are asked to find out how long it would take if they work together.
- The Work Problem Concept:
STEP 1: Calculate how much work each person/machine does in one unit of time (could be days, hours, minutes, etc.)
 If we are given that A completes a certain amount of work in X hours, simply reciprocate the number of hours to get the per hour work. Thus, in one hour, A would complete
If we are given that A completes a certain amount of work in X hours, simply reciprocate the number of hours to get the per hour work. Thus, in one hour, A would complete 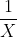 of the work. But what is the logic behind this?
of the work. But what is the logic behind this?
 Let me explain with the help of an example.
Let me explain with the help of an example.
 Assume we are given that Jack paints a wall in 5 hours. This means that in every hour, he completes a fraction of the work so that at the end of 5 hours, the fraction of work he has completed will become 1 (that means he has completed the task).
Assume we are given that Jack paints a wall in 5 hours. This means that in every hour, he completes a fraction of the work so that at the end of 5 hours, the fraction of work he has completed will become 1 (that means he has completed the task).
 Thus, if in 5 hours the fraction of work completed is 1, then in 1 hour, the fraction of work completed will be (1*1)/5
Thus, if in 5 hours the fraction of work completed is 1, then in 1 hour, the fraction of work completed will be (1*1)/5
STEP 2: Add up the amount of work done by each person/machine in that one unit of time.
 This would give us the total amount of work completed by both of them in one hour. For example, if A completes
This would give us the total amount of work completed by both of them in one hour. For example, if A completes 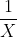 of the work in one hour and B completes
of the work in one hour and B completes 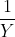 of the work in one hour, then TOGETHER, they can complete
of the work in one hour, then TOGETHER, they can complete  of the work in one hour.
of the work in one hour.
STEP 3: Calculate total amount of time taken for work to be completed when all persons/machines are working together.
 The logic is similar to one we used in STEP 1, the only difference being that we use it in reverse order.
The logic is similar to one we used in STEP 1, the only difference being that we use it in reverse order.
 Suppose
Suppose 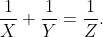
 This means that in one hour, A and B working together will complete
This means that in one hour, A and B working together will complete 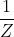 of the work. Therefore, working together, they will complete the work in Z hours.
of the work. Therefore, working together, they will complete the work in Z hours.
Example-1:
 Jack can paint a wall in 3 hours. John can do the same job in 5 hours. How long will it take if they work together?
Jack can paint a wall in 3 hours. John can do the same job in 5 hours. How long will it take if they work together?
Solution:
 This is a simple straightforward question wherein we must just follow steps 1 to 3 in order to obtain the answer.
This is a simple straightforward question wherein we must just follow steps 1 to 3 in order to obtain the answer.
 STEP 1: Calculate how much work each person does in one hour.
STEP 1: Calculate how much work each person does in one hour.
 Jack → (1/3) of the work
Jack → (1/3) of the work
 John → (1/5) of the work
John → (1/5) of the work
 STEP 2: Add up the amount of work done by each person in one hour.
STEP 2: Add up the amount of work done by each person in one hour.
 Work done in one hour when both are working together
Work done in one hour when both are working together 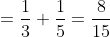
 STEP 3: Calculate total amount of time taken when both work together.
STEP 3: Calculate total amount of time taken when both work together.
 If they complete 8/15 of the work in 1 hour, then they would complete 1 job in 15/8 hours.
If they complete 8/15 of the work in 1 hour, then they would complete 1 job in 15/8 hours.
Example-2:
 Working, independently X takes 12 hours to finish a certain work. He finishes 2/3 of the work. The rest of the work is finished by Y whose rate is 1/10 of X. In how much time does Y finish his work?
Working, independently X takes 12 hours to finish a certain work. He finishes 2/3 of the work. The rest of the work is finished by Y whose rate is 1/10 of X. In how much time does Y finish his work?
Solution:
 Now the only reason this is trickier than the first problem is because the sequence of events is slightly more complicated. The concept however is the same. So, if our understanding of the concept is clear, we should have no trouble at all dealing with this.
Now the only reason this is trickier than the first problem is because the sequence of events is slightly more complicated. The concept however is the same. So, if our understanding of the concept is clear, we should have no trouble at all dealing with this.
 ‘Working, independently X takes 12 hours to finish a certain work’ This statement tells us that in one hour, X will finish 1/12 of the work.
‘Working, independently X takes 12 hours to finish a certain work’ This statement tells us that in one hour, X will finish 1/12 of the work.
 ‘He finishes 2/3 of the work’, This tells us that 1/3 of the work still remains.
‘He finishes 2/3 of the work’, This tells us that 1/3 of the work still remains.
 ‘The rest of the work is finished by Y whose rate is (1/10) of X’ Y has to complete 1/3 of the work.
‘The rest of the work is finished by Y whose rate is (1/10) of X’ Y has to complete 1/3 of the work.
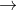 ‘Y's rate is (1/10) that of X‘. We have already calculated rate at which X works to be 1/12. Therefore, rate at which Y works is
‘Y's rate is (1/10) that of X‘. We have already calculated rate at which X works to be 1/12. Therefore, rate at which Y works is 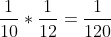
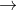 ‘In how much time does Y finish his work?’ If Y completes 1/120 of the work in 1 hour, then he will complete 1/3 of the work in 40 hours.
‘In how much time does Y finish his work?’ If Y completes 1/120 of the work in 1 hour, then he will complete 1/3 of the work in 40 hours.
 So, as you can see, even though the question might have been a little difficult to follow at first reading, the solution was in fact quite simple. We didn’t use any new concepts. All we did was apply our knowledge of theconcept we learnt earlier to the information in the question in order to answer what was being asked.
So, as you can see, even though the question might have been a little difficult to follow at first reading, the solution was in fact quite simple. We didn’t use any new concepts. All we did was apply our knowledge of theconcept we learnt earlier to the information in the question in order to answer what was being asked.
Example-3:
 Working together, printer A and printer B would finish a task in 24 minutes. Printer A alone would finish the task in 60 minutes. How many pages does the task contain if printer B prints 5 pages a minute more than printer A?
Working together, printer A and printer B would finish a task in 24 minutes. Printer A alone would finish the task in 60 minutes. How many pages does the task contain if printer B prints 5 pages a minute more than printer A?
Solution:
 This problem is interesting because it tests not only our knowledge of the concept of word problems, but also our ability to ‘translate English to Math’ ‘Working together, printer A and printer B would finish a task in 24 minutes’ This tells us that A and B combined would work at the rate of 1/24 per minute.
This problem is interesting because it tests not only our knowledge of the concept of word problems, but also our ability to ‘translate English to Math’ ‘Working together, printer A and printer B would finish a task in 24 minutes’ This tells us that A and B combined would work at the rate of 1/24 per minute.
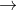 ‘Printer A alone would finish the task in 60 minutes’ This tells us that A works at a rate of 1/60 per minute.
‘Printer A alone would finish the task in 60 minutes’ This tells us that A works at a rate of 1/60 per minute.
 At this point, it should strike you that with just this much information, it is possible to calculate the rate at which B works:
At this point, it should strike you that with just this much information, it is possible to calculate the rate at which B works:
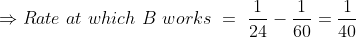
 ‘B prints 5 pages a minute more than printer A’ This means that the difference between the amount of work B and
‘B prints 5 pages a minute more than printer A’ This means that the difference between the amount of work B and
 A complete in one minute corresponds to 5 pages. So, let us calculate that difference.
A complete in one minute corresponds to 5 pages. So, let us calculate that difference.
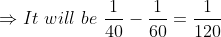
 ‘How many pages does the task contain?’ If 1/120 of the job consists of 5 pages, then the 1 job will consist of
‘How many pages does the task contain?’ If 1/120 of the job consists of 5 pages, then the 1 job will consist of }{\frac{1}{120}}=600\&space;pages.)
Example-4:
Machine A and Machine B are used to manufacture 660 sprockets. It takes machine A ten hours longer to produce 660 sprockets than machine B.
Machine B produces 10% more sprockets per hour than machine A. How many sprockets per hour does machine A produce?
Solution:
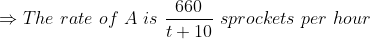
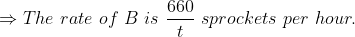
We are told that B produces 10% more sprockets per hour than A, thus
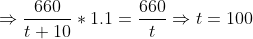
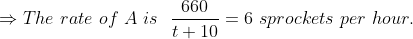
128 Time and Work - Trick #134
N/A
If M1 men can finish W1 work in D1 days and M2 men can finish M2 work in D2 days then, Relation is
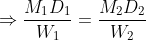
If M1 men finish W1 work in D1 days, working T1 time each day and M2 men finish W2 work in D2 days, working T2 time each day, then
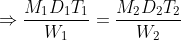
129 Time and Work - Trick #135
N/A
If A completes a piece of work in ‘x’ days, and B completes the same work in ‘y’ days, then,
Work done by A in 1 day = 1/x, Work done by B in 1 day = 1/y
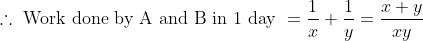
)
130 Time and Work - Trick #136
N/A
If A can do a work in ‘x’ days, B can do the same work in ‘y’ days, C can do the same work in ‘z’ days then, total time taken by A, B and C to complete
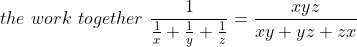
If workers are more than 3 then total time taken by A, B, C ...... so on to
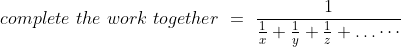
Example:
A, B and C individually can do a work in 10 days, 12 days and 15 days respectively. If they start working together, then the number of days required to finish the work is?
Solution:
By Applying Trick 136,
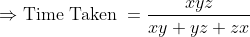
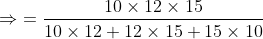

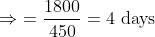
131 Time and Work - Trick #137
N/A
If A alone can do a certain work in ‘x’ days and A and B together can do the same work in ‘y’ days, then B alone can do the same work in
\mathrm{\&space;days})
Example:
A and B together can dig a trench in 12 days, which A alone can dig in 28 days; B alone can dig it in
Solution:
By Applying Trick 137,
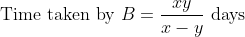
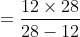
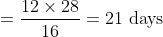
132 Time and Work - Trick #138
N/A
If A and B can do a work in ‘x’ days, B and C can do the same work in ‘y’ days, C and A can do the same work in ‘z’ days.
Then total time taken, when A, B and C work together
}\mathrm{\&space;OR\&space;}\frac{2xyz}{xy+yz+zx}\&space;days)
Example:
A and B can do a given piece of work in 8 days, B and C can do the same work in 12 days and A, B, C complete it in 6 days. Number of days required to finish the work by A and C is?
Solution:
By Applying Trick 138,
Let the time taken by A and C is x days
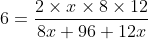
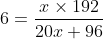
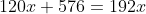
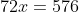

133 Time and Work - Trick #139
N/A
Total work = (work of one day) × (total no. of working days) Remaining
Work = 1 – (work done)
Work done by A = (Work done in 1 day by A) × (total no. of days worked by A, B and C and so on
})
Where A can complete work in x days, B in y days, C in z days and so on.
134 Time and Work - Trick #140
N/A
If A can finish m/n part of the work in D days. Then, Total time taken to finish the work by
}=\frac{n}{m}\times&space;D\mathrm{\&space;days})
135 Time and Work - Trick #141
N/A
(i) If A can do a work in ‘x’ days and B can do the same work in ‘y’ days and when they started working together, B left the work ‘m’ days before
x}{x+y})
(ii) A leaves the work ‘m’ days before its completion then total time taken
y}{x+y})
Example-1:
A can do a piece of work in 18 days and B in 12 days. They began the work together, but B left the work 3 days before its completion. In how many days, in all, was the work completed?
Solution:
By Applying Trick 141(i),
Here, x = 18, y = 12, m = 3
x)
\times18=9\mathrm{\&space;days})
Example-2:
A and B alone can complete work in 9 days and18 days respectively. They worked together; however, 3 days before the completion of the work A left. In how many days was the work completed?
Solution:
By Applying Trick 141(ii),
Here, x = 9, y = 18, m = 3
Total time taken
y}{x+y})
\times18}{9+18})
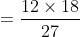
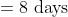
136 Time and Work - Trick #142
N/A
If A and B together can finish a certain work in ‘a’ days. They worked together for ‘b’ days and then ‘B’ (or A) left the work. A (or B) finished the rest work in ‘d’ days, then Total time taken by A (or B) alone to complete the work
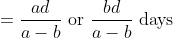
Example:
A and B can together finish a work in 30 days. They worked at it for 20 days and then B left. The remaining work was done by A alone in 20 more days.
A alone can finish the work in?
Solution:
By Applying Trick 142,
Here, a = 30, b = 20, d = 20
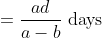
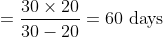
137 Time and Work - Trick #144
N/A
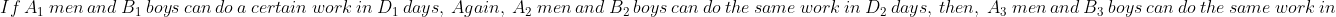
![Required\ time=\frac{D_1D_2\left[A_1B_2-A_2B_1\right]}{D_1\left[A_1B_3-A_3B_1\right]-D_2\left[A_2B_3-A_3B_2\right]}\mathrm{\ days}](https://latex.codecogs.com/gif.latex?Required\&space;time=\frac{D_1D_2\left[A_1B_2-A_2B_1\right]}{D_1\left[A_1B_3-A_3B_1\right]-D_2\left[A_2B_3-A_3B_2\right]}\mathrm{\&space;days})
Example:
4 men and 6 women can complete a work in 8 days, while 3 men and 7 women can complete it in 10 days. In how many days will 10 women complete it?
Solution:
By Applying Trick 144,

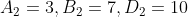
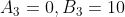
![Required\ time=\frac{D_1D_2\left[A_1B_2-A_2B_1\right]}{D_1\left[A_1B_3-A_3B_1\right]-D_2\left[A_2B_3-A_3B_2\right]}](https://latex.codecogs.com/gif.latex?Required\&space;time=\frac{D_1D_2\left[A_1B_2-A_2B_1\right]}{D_1\left[A_1B_3-A_3B_1\right]-D_2\left[A_2B_3-A_3B_2\right]})
}{8(4\times10-0\times6)-10(3\times10-0\times7)})

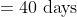
138 Time and Work - Trick #143
N/A
If food is available for ‘a’ days for ‘A’ men at a certain place and after ‘b’ days. ‘B’ men join, then the remaining food will serve total men for
}{(A+B)}\mathrm{\&space;days})
If food is available for ‘a’ days for ‘A’ men at a certain place, and after ‘b’ days ‘B’ men leave then the remaining food will serve remaining men for
}{(A-B)}\mathrm{\&space;days})
Example:
40 men can complete a work in 18 days. Eight days after they started working together, 10 more men joined them. How many days will they now take to complete the remaining work?
Solution:
By Applying Trick 143,
Here, A = 40, a = 18
b = 8, B = 10
}{A+B})
}{40+10})

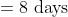
139 Time and Work - Trick #145
N/A
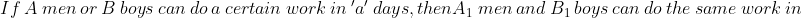
}{A_1B+B_1A}\&space;\&space;days)
Example:
If 8 men or 12 boys can do a piece of work in 16 days, the number of days required to complete the work by 20 men and 6 boys is?
Solution:
Here, A = 8, B = 12, a = 16
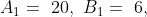
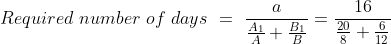
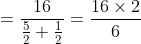
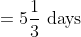
140 Time and Work - Trick #146
N/A
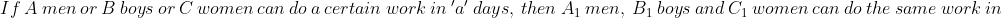
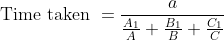
Example:
If 1 man or 2 women or 3 boys can complete a piece of work in 88 days,then 1 man, 1 woman and 1 boy together will complete it in?
Solution:
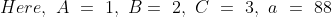

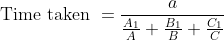
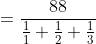
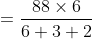
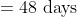
141 Time and Work - Trick #147
N/A
If ‘A’ men can do a certain work in ‘a’ days and ‘B’ women can do the same work in ‘b’ days, then the total time taken when A1 men and B1 women work together is
})

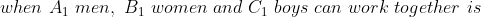
})
Example-1:
5 men can do a piece of work in 6 days while 10 women can do it in 5 days.
In how many days can 5 women and 3 men do it?
Solution:
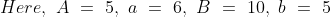
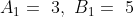
})
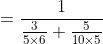
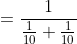
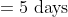
Example-2:
A man, a woman and a boy can complete a work in 20 days, 30 days and 60 days respectively. How many boys must assist 2 men and 8 women so as to complete the work in 2 days?
Solution:
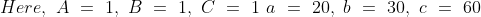
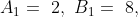
})
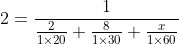

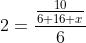
142 Time and Work - Trick #148
N/A
The comparison of rate of work done is called efficiency of doing work.
\propto\frac{1}{\mathrm{\&space;No.\&space;of\&space;days\&space;}})
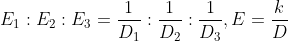
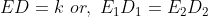
Example:
Mike can do a work in 15 days. John is 50 per cent more efficient than
Mike in doing the work. In how many days will John do that work?
Solution:
Efficiency and time taken are inversely proportional
)
\&space;}=2:3)
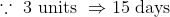
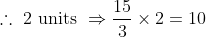
Hence, John completes the work in 10 days.
143 Time and Work - Trick #149
N/A
If the efficiency to work of A is twice the efficiency to work of B, then,
=\&space;2x\&space;:&space;x\&space;and\&space;A\&space;:&space;B\&space;\left(time\right)=\&space;t\&space;:2t)
Example:
A man and a boy received $800 as wages for 5 days for the work they did
together. The man’s efficiency in the work was three times that of the boy.
What are the daily wages of the boy?
Solution:
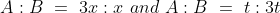
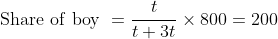
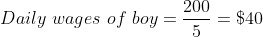
144 Time and Work - Trick #150
N/A
If A can do a work in ‘x’ days and B is R% more efficient than A, then ‘B’ alone will do the same work in
}\mathrm{\&space;days})
Example:
A can do a piece of work in 70 days and B is 40% more efficient than A. The number of days taken by B to do the same work is?
Solution:
Here, x = 70, r = 40%

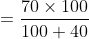
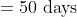
145 Time and Work - Trick #151
N/A
A, B and C can do a certain work together within ‘x’ days. While, any two of them can do the same work separately in ‘y’ and ‘z’ days, then in how many days can 3rd do the same work
}\mathrm{\&space;days})
Example:
A, B and C can complete a work in 8 days. B alone can do it in 18 days and C alone can do it in 24 days. In how many days can A alone do the same work?
Solution:
Here, x = 8, y = 18, z = 24
})
})

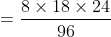
146 Time and Work - Trick #152
N/A
A and B can do a work in ‘x’ days, B and C can do the same work in ‘y’ days. C and A can do the same work in ‘z’ days.
Then, all can do alone the work as following:
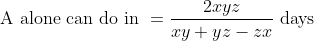

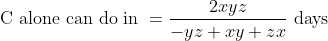
Example-1:
A and B can do a piece of work in 10 days. B and C can do it in 12 days. A and C can do it in 15 days. How long will A take to do it alone?
Solution:
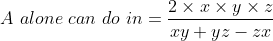
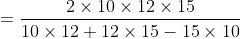
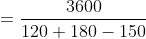
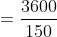
Example-2:
If A and B together can complete a work in 18 days, A and C together in 12 days and B and C together in 9 days, then B alone can do the work in?
Solution:

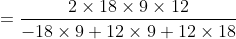
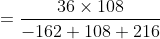
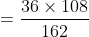
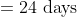
Example-3:
A and B can do a piece of work in 10 days. B and C can do it in 12 days. C and A in 15 days. In how many days will C finish it alone?
Solution:
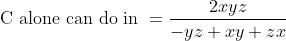
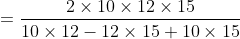
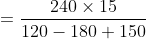

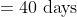
147 Time and Work - Trick #153
N/A
A can do a certain work in ‘m’ days and B can do the same work in ‘n’ days.
They worked together for ‘P’ days and after this A left the work, then in how many days did B alone do the rest of work
}{m}\mathrm{\&space;days})
when after ‘P’ days B left the work, then in how many days did A alone do the rest of work
}{n}\mathrm{\&space;days})
Example-1:
A can do a piece of work in 12 days and B in 15 days. They work together for 5 days and then B left. The days taken by A to finish the remaining work is?
Solution:
Here, m = 12, n = 15, p = 5
}{n}\mathrm{\&space;days\&space;})
}{15})
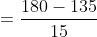
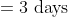
Example-2:
A can do a piece of work in 12 days and B can do it in 18 days. They work together for 2 days and then A leaves. How long will B take to finish the remaining work?
Solution:
Here, m = 12, n = 18, p = 2
Time taken by B
}{m})
}{12})
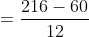
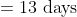
148 Time and Work - Trick #154
N/A

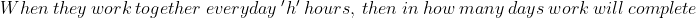
![\mathrm{\ Required\ time\ }=\left[\frac{\left(h_1d_1\right)\times\left(h_2d_2\right)}{\left(h_1d_1+h_2d_2\right)}\right]\frac{1}{h}](https://latex.codecogs.com/gif.latex?\mathrm{\&space;Required\&space;time\&space;}=\left[\frac{\left(h_1d_1\right)\times\left(h_2d_2\right)}{\left(h_1d_1+h_2d_2\right)}\right]\frac{1}{h})
Example:
While working 7 hours a day, A alone can complete a piece of work in 6 days and B alone in 8 days. In what time would they complete it together, working 8 hours a day?
Solution:
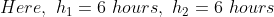
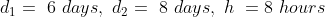
![\mathrm{Required\ time\ }=\left[\frac{\left(h_1d_1\right)\times\left(h_2d_2\right)}{\left(h_1d_1+h_2d_2\right)}\right]\frac{1}{h}](https://latex.codecogs.com/gif.latex?\mathrm{Required\&space;time\&space;}=\left[\frac{\left(h_1d_1\right)\times\left(h_2d_2\right)}{\left(h_1d_1+h_2d_2\right)}\right]\frac{1}{h})
![=\left[\frac{(6\times6)\times(6\times8)}{6\times6+6\times8}\right]\times\frac{1}{8}](https://latex.codecogs.com/gif.latex?=\left[\frac{(6\times6)\times(6\times8)}{6\times6+6\times8}\right]\times\frac{1}{8})
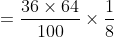

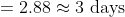
149 Time and Work - Trick #155
N/A
The efficiency of A to work is ‘n’ times more than that of B, both start to work together and finish it in ‘D’ days. Then, A and B will separately complete, the work in
D\mathrm{\&space;and\&space;}(n+1)D\mathrm{\&space;days\&space;respectively.})
Example:
A can do in one day three times the work done by B in one day. They together finish 2/5 of the work in 9 days. The number of days by which B can do the work alone is?
Solution:
Here, n = 3 and D
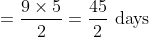
(Time taken to finish whole work)
D)
\times\frac{45}{2})
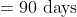
150 Time and Work - Trick #156
N/A
Some people finish a certain work in ‘D’ days. If there were ‘a’ less people, then the work would be completed in ‘d’ days more, what was the number of people initially
}{d}\mathrm{\&space;people})
Example:
A certain number of persons can complete a piece of work in 55 days. If there were 6 persons more, the work could be finished in 11 days less. How many persons were originally there?
Solution:
Here, D = 55
a = 6, d = 11
}{d})
}{11}=24)
151 Time and Work - Trick #157
N/A
A can do a work in ‘m’ days and B can do the same work in ‘n’ days. If they work together and total wages is R, then
}\times&space;R)
}\times&space;R)
Example:
Adam can do a work in 3 days. Wade can do the same work in 2 days.
Both of them finish the work together and get 150. What is the share of Adam?
Solution:
Here, m = 3, n = 2, R = 150
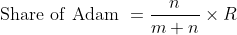
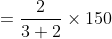
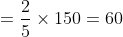
152 Time and Work - Trick #158
N/A
If A, B and C finish the work in m, n and p days respectively and they receive the total wages R, then the ratio of their wages is

Example:
‘A’ alone can do a piece of work in 6 days and ‘B’ alone in 8 days. A and B undertook to do it for $3200. With the help of ‘C’, they completed the work in 3 days. How much is to be paid to C?
Solution:
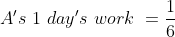
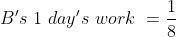
's\&space;1\&space;day's\&space;work&space;=13)
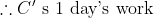
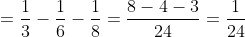

Sum of the ratios = 4 + 3 + 1 = 8

153 Time and Work - Trick #159
N/A
A and B can do a piece of work in x and y days, respectively. Both begin together but after some days. A leaves the job and B completed the remaining work in a days. After how many days did A leave?
}{x+y}\times&space;x)
Example:
A and B can do a work in 45 days and 40 days respectively. They began the work together but A left after some time and B completed the remainingwork in 23 days. After how many days of the start of the work did A leave?
Solution:
Here, x = 45, y = 40, a = 23
}{(x+y)}\times&space;x)
\times45}{45+40})
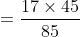
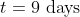
154 Time and Work - Trick #160
N/A
If A men and B boys can complete a work in x days, while A, men and B, boys will complete the same work in y days, then
}{\left(xA-yA_1\right)})
155 Profit and Loss: Formula
N/A
\\)
156 Profit and Loss - Trick #161
N/A
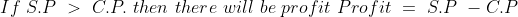
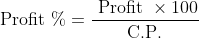
Note: Both profit and loss are always calculated on cost price only
Example-1:
A man bought an old typewriter for $1200 and spent $200 on its repair. He sold it for $1680. His profit percent is?
Solution:
\&space;=$\$&space;1400\)
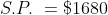
&space;=$\$&space;280)
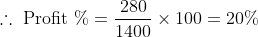
Example-2:
A merchant buys an article for $27 and sells it at a profit of 10% of the selling price. The selling price of the article is?
Solution:
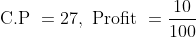
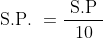
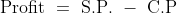


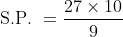

157 Profit and Loss - Trick #162
N/A
If C.P > S.P., then there will be Loss
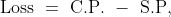
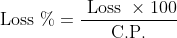
Example-1:
Mike had to sell vegetables worth $5,750 for $4,500 due to heavy rainfall.
What is the loss percentage that he has incurred?
Solution:
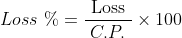
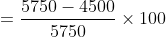
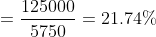
Example-2:
If a shop–keeper purchases cashew nut at $250 per kg. and sells it at $10 per 50 grams, then he will have?
Solution:
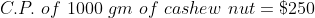
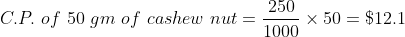
S.P. of 50 gm of cashew nut = $10

158 Profit and Loss - Trick #163
N/A
If an object is sold on r% Profit.
![\mathrm{then\ S.P.\ }=\mathrm{\ C.P\ }\left[\frac{100+\mathrm{\ Profit\ }%}{100}\right]](https://latex.codecogs.com/gif.latex?\mathrm{then\&space;S.P.\&space;}=\mathrm{\&space;C.P\&space;}\left[\frac{100+\mathrm{\&space;Profit\&space;}%}{100}\right])
![C.P=\mathrm{\ S.P.\ }\left[\frac{100}{100+\mathrm{\ Profit\ }%}\right]](https://latex.codecogs.com/gif.latex?C.P=\mathrm{\&space;S.P.\&space;}\left[\frac{100}{100+\mathrm{\&space;Profit\&space;}%}\right])
Similarly, if an object is sold on r% loss, then
![\mathrm{S.P.\ }=\left[\frac{100-Loss%}{100}\right]\mathrm{\ }](https://latex.codecogs.com/gif.latex?\mathrm{S.P.\&space;}=\left[\frac{100-Loss%}{100}\right]\mathrm{\&space;})
![\text { or C.P. }=\text { S.P. }\left[\frac{100}{100-\text { Loss } \%}\right]](https://latex.codecogs.com/gif.latex?\text&space;{&space;or&space;C.P.&space;}=\text&space;{&space;S.P.&space;}\left[\frac{100}{100-\text&space;{&space;Loss&space;}&space;\%}\right])
Example-1:
A man buys a cycle for $1400 and sells it at a loss of 15%. What is the selling price of the cycle?
Solution:
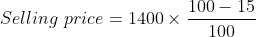
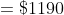
Example-2:
On selling an article for $651, there is a loss of 7%. The cost price of that article is?
Solution:
)
)
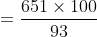
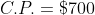
159 Profit and Loss - Trick #164
N/A
Successive Profits: If A sells an article to B at a% profit and B sells it to C at b% profit
OR
If a% and b% are two successive profits
%)
If A sells an article to B at a% profit and B sells it to C at b% profit and if C paid $x, then amount paid by
\left(\frac{100}{100+b}\right))
160 Profit and Loss - Trick #165
N/A
If a% and b% are two successive losses then (negative sign shows loss and positive sign shows profit)
&space;\%)
Example:
If a certain company undergoes losses of 10% and 5% in the first two months of the year, then total loss percent for the two months is?
Solution:
&space;\%)
%)
%)
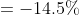
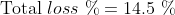
Negative sign shows decrease
161 Profit and Loss - Trick #166
N/A
If a% profit and b% loss occur, simultaneously then overall loss or profit% %)
)
Example:
If a certain company undergoes profit of 20% for March and loss of 10% for April months of the year, then total loss/profit percent for the two months is?
Solution:
By Applying Trick 166,
%)
%)
%)
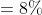
Therefore 8% profit
Positive sign shows increase
162 Profit and Loss - Trick #167
N/A
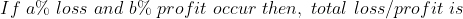
%\)
)
Example:
When the price of cloth was reduced by 25%, the quantity of cloth sold increased by 20%. What was the effect on gross receipt of the shop?
Solution:
Required per cent effect
%)
%&space;=&space;-&space;10%&space;(10%&space;decrease))
Negative sign shows decrease
163 Profit and Loss - Trick #168
N/A
If cost price of ‘x’ articles is equal to selling price of ‘y’ articles, then Selling
Price = x, Cost Price = y
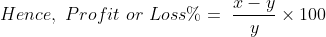
Example:
The cost price of 15 articles is same as the selling price of 10 articles. The profit percent is?
Solution:
Here, x = 15, y = 10
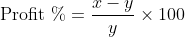
\times100)

164 Profit and Loss - Trick #169
N/A
On selling ‘x’ articles the profit or loss is equal to Selling of ‘y’ articles, then
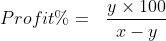

Example:
A cloth merchant on selling 33 metres of cloth obtains a profit equal to the selling price of 11 metres of cloth. The profit percent is?
Solution:
Here, x = 33, y = 11
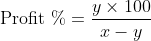



165 Profit and Loss - Trick #170
N/A
If a man sells two similar objects, one at a loss of x% and another at a gain of x%, then he always incurs loss in this transaction and loss% is 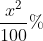
Example:
A cloth merchant on selling 33 metres of cloth obtains a profit equal to the selling price of 11 metres of cloth. The profit percent is?
Solution:
Here, selling prices are same, Profit-loss percent are same. In such transactions, there is always loss.
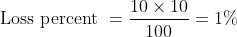
166 Profit and Loss - Trick #171
N/A
A man sells his items at a profit/loss of x%. If he had sold it for $R more, he would have gained/lost y%. Then.
}&space;\times&space;100)
‘+’ = When one is profit and other is loss.
‘–’ = When both are either profit or loss.
Example:
A man sold his watch at a loss of 5%. Had he sold it for $56.25 more, he would have gained 10%. What is the cost price of the watch (in $)?
Solution:
Here, x = 5%, R = 56.25, y = 10%
\times100)
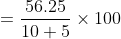
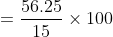
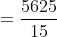

If a man purchases ‘a’ items for $x and sells ‘b’ items for $y, then his profit or loss per cent is given by
\times100%)
)
Example:
If a man purchases 5 articles for $120 and sells 10 articles for $80, then his profit or loss percent is?
Solution:
\times100%)
\times100%)
\times100%)
\times100%)
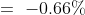
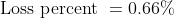
167 Profit and Loss - Trick #172
N/A
If a man purchases ‘a’ items for $x and sells ‘b’ items for $y, then his profit or loss per cent is given by
\times100%)
)
Example:
If a man purchases 5 articles for $120 and sells 10 articles for $80, then his profit or loss percent is?
Solution:
\times100%)
\times100%)
\times100%)
\times100%)
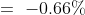
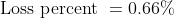
168 Profit and Loss - Trick #173
N/A
If the total cost of ‘a’ articles having equal cost is $x and the total selling price of ‘b’ articles is $y, then in the transaction gain or loss per cent is given by
\times100%)
Where positive value signifies ‘profit’ and negative value signifies ‘loss’
Example:
Ten articles were bought for $8, and sold at 8 for $10. The gain percent is?
Solution:
\times100%)
\times100%)
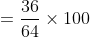
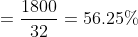
169 Profit and Loss - Trick #174
N/A
A dishonest shopkeeper sells his goods at C.P. but uses false weight, then his
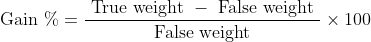
or

Example-1:
A dishonest fruit vendor sells his goods at cost price but he uses a weight of 900 gm for a kg. weight. His gain per cent is?
Solution:
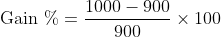
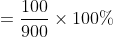
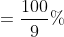
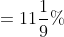
Example-2:
A dishonest dealer professes to sell his goods at the cost price but uses a false weight of 850 g instead of 1 kg. His gain percent is?
Solution:
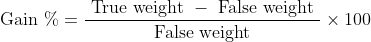
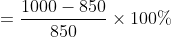
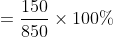

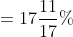
170 Profit and Loss - Trick #175
N/A
If A sells an article to B at a profit (loss) of 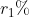 and B sells the same article to C at a profit (loss) of
and B sells the same article to C at a profit (loss) of 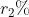 then the cost price of article for C will be given by C.P of article for C
then the cost price of article for C will be given by C.P of article for C
\left(1\pm\frac{r_2}{100}\right))
(Positive and negative sign conventions are used for profit and loss.)
Example:
David sold a Car at 20% gain to Jenny. Jenny sold it to John at 10% profit. If John had to pay $33,000 for the Car, find the cost price of the Car for David?
Solution:
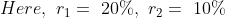
C.P. for John = C.P. for David
\left(1+\frac{r_2}{100}\right))
33000 = C.P. for David
\left(1+\frac{10}{100}\right))
C.P. for David =
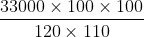
= $25,000
171 Profit and Loss - Trick #176
N/A
If a vendor used to sell his articles at x% loss on cost price but uses y grams instead of z grams, then his profit or loss% is
![\left[(100-x)\frac{z}{y}-100\right]%](https://latex.codecogs.com/gif.latex?\left[(100-x)\frac{z}{y}-100\right]%)
(Profit or loss as per positive or negative sign).
172 Boats and Streams: Formula
N/A
If the speed of certain swimmer (or boat or ship) in still water is v km/h and the speed of stream is u km/h, then
(i) The speed of swimmer or boat or ship in the direction of
\&space;=\&space;(u\&space;+\&space;v)\&space;km/h)
(ii) The speed of swimmer or boat or ship in the opposite direction of
\&space;=(v\&space;-&space;u)&space;km/h)
173 Boats and Streams - Trick #177
N/A
If the speed of a swimmer/boat/ship in the direction of stream (downstream) is x km/h and in the opposite direction of stream (upstream) is y km/h, then,
\&space;Speed\&space;of\&space;swimmer/boat/ship\&space;}=\frac{x+y}{2}km/h)
\&space;Speed\&space;of\&space;stream\&space;}=\frac{x-y}{2}km/h)
Example-1:
A boatman rows 1 km in 5 minutes, along the stream and 6 km in 1 hour against the stream. The speed of the stream is?
Solution:
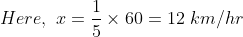

)
)
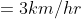
Example-2:
A man rows 40 km upstream in 8 hours and a distance of 36 km downstream in 6 hours. Then speed of stream is
Solution:
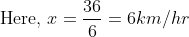
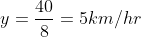
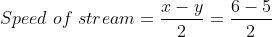
= 0.5 km/hr
Example-3:
A boat travels 24 km upstream in 6 hours and 20 km downstream in 4 hours. Then the speed of boat in still water and the speed of water current are respectively
Solution:



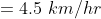
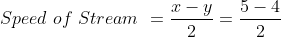
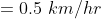
174 Boats and Streams - Trick #178
N/A
Let the speed of boat is x km/h and speed of stream is y km/h. To travel 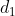 km downstream and
km downstream and 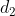 km upstream, the time taken is ‘t’ hours, then
km upstream, the time taken is ‘t’ hours, then
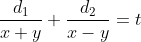
Example:
A boat covers 12 km upstream and 18 km downstream in 3 hours, while it covers 36 km upstream and 24 km downstream in 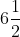 hours.
hours.
What is the speed of the current?
Solution:
Let the speed of boat in still water be x kmph and that of current be y kmph, then
)
)
By equation (i) × 3 – equation (ii),
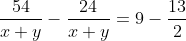
})
From equation (i),
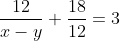

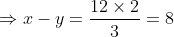
=2\&space;kmph)
175 Boats and Streams - Trick #179
N/A
Let the speed of stream be y km/h and speed of boat be x km/h.
A boat travels equal distance upstream as well as downstream in ‘t’ hours, then
}{2x})
Example:
A boat goes 12 km downstream and comes back to the starting point in 3 hours. If the speed of the current is 3 km/hr, then the speed (in km/hr) of the boat in still water is?
Solution:
Let the speed of boat in still water be x kmph, then
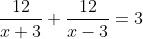
(x-3)}\right)=3)
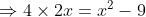
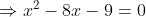
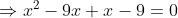
+1(x-9)=0)
(x+1)=0)
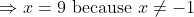
Therefore, Speed can't be negative.
Hence, speed of boat in still water = 9 kmph
176 Boats and Streams - Trick #180
N/A
If a boat travels in downstream and upstream, then,

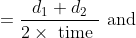

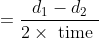
177 Boats and Streams - Trick #181
N/A
A swimmer or a boat travels a certain distance upstream in 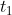 hours, while it takes
hours, while it takes 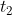 hours to travel same distance downstream, then,
hours to travel same distance downstream, then,
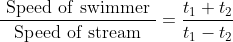
Example:
A boat goes 6 km an hour in still water, but takes thrice as much time in going the same distance against the current. The speed of the current (in km/hour) is?
Solution:
Here, Speed of boat = 6 km/hr
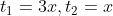

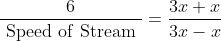
Speed of current = 3 km/hr
178 Boats and Streams - Trick #182
N/A
If a swimmer takes same time to travel  km downstream and
km downstream and  km upstream, then,
km upstream, then,
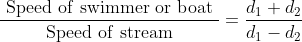
179 Boats and Streams - Trick #183
N/A
If a man or a boat covers x km distance in 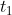 hours along the direction of stream (downstream) and covers the same distance in
hours along the direction of stream (downstream) and covers the same distance in 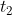 hours against the stream i.e., upstream, then
hours against the stream i.e., upstream, then
km/hr)
km/hr)
Example-1:
A boat goes 6 km an hour in still water, but takes thrice as much time in going the same distance against the current. The speed of the current (in km/hour) is?
Solution:
)
)
)
= 1.5 km/hr
Example-2:
A man can row 30 km downstream and return in a total of 8 hours. If the speed of the boat in still water is four times the speed of the current, then the speed of the current is?
Solution:
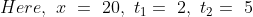
)
=7km/hr)
180 Boats and Streams - Trick #183
N/A
If the speed of a boat or swimmer in still water is a km/hr and river is flowing with a speed of b km/hr, then average speed in going to a certain place and coming back to starting point is given by
(a-b)}{a}\&space;km/hr)
Example-1:
A man can row 30 km downstream and return in a total of 8 hours. If the speed of the boat in still water is four times the speed of the current, then the speed of the current is?
Solution:
Here, a = 5, b = 1
(a-b)}{a})
(5-1)}{5})
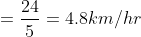

181 Pipe and Cistern - Formula
N/A
There are two types of taps:
Tap to fill the water (efficiency +) (inlet)
Tap to release the water (efficiency –) (outlet)
182 Pipe and Cistern - Trick #184
N/A
Two taps ‘A’ and ‘B’ can fill a tank in ‘x’ hours and ‘y’ hours respectively. If both the taps are opened together, then the time it will take to fill the tank is
hrs)
Example-1:
Two pipes A and B can fill a tank in 20 minutes and 30 minutes respectively. If both pipes are opened together, the time taken to fill the tank is?
Solution:
Here, x = 20, y = 30
Required time
\mathrm{\&space;minutes})
\mathrm{\&space;minutes})
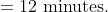
Example-2:
Two pipes can fill a cistern separately in 10 hours and 15 hours. They can together fill the cistern in?
Solution:
Part of the cistern filled by both pipes in 1 hour
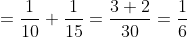
The cistern will be filled in 6 hours.
183 Pipe and Cistern - Trick #185
N/A
If x, y, z, ........... all taps are opened together then, the time required to fill/empty the tank will be:

where T, is the required time
Example-1:
Two pipes A and B can fill a cistern in 3 hours and 5 hours respectively.
Pipe C can empty in 2 hours. If all the three pipes are open, in how many hours the cistern will be full?
Solution:
Part of cistern filled by three pipes in an hour
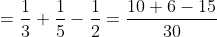
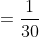
Hence, the cistern will be filled in 30 hours.
Example-2:
Two pipes can fill a tank in 15 hours and 20 hours respectively, while the third can empty it in 30 hours. If all the pipes are opened simultaneously, the empty tank will be filled in?
Solution:
Part of tank filled in 1 hour when all three pipes are opened simultaneously
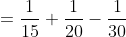
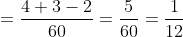
184 Pipe and Cistern - Trick #186
N/A
Two taps can fill a tank in ‘x’ and ‘y’ hours respectively. If both the taps are opened together and 1st tap is closed before ‘m’ hours of filling the tank, then in how much time the tank will be filled
y}{(x+y)}hrs)
If 2nd tap is closed before ‘m’ hours then
x}{(x+y)}hrs)
185 Pipe and Cistern - Trick #187
N/A
If a pipe fills a tank in ‘x’ hours but it takes ‘t’ more hours to fill it due to leakage in tank. If tank is filled completely, then in how many hours it will be empty? [due to leakage outlet]
}{t})
186 Pipe and Cistern - Trick #188
N/A
Amount of water released or filled = Rate × time.
187 Pipe and Cistern - Trick #189
N/A
Two taps ‘A; and ‘B’ can empty a tank in ‘x’ hours and ‘y’ hours respectively.
If both the taps are opened together, then time taken to empty the tank will be
\mathrm{\&space;hrs})
Example-1:
A tap can empty a tank in one hour. A second tap can empty it in 30 minutes. If both the taps operate simultaneously, how much time is needed to empty the tank?
Solution:
Here, x = 60, y = 30
\mathrm{\&space;minutes})
\mathrm{\&space;minutes})
= 20 minutes
Example-2:
A tap can empty a tank in 30 minutes. A second tap can empty it in 45 minutes. If both the taps operate simultaneously, how much time is needed to empty the tank?
Solution:
Part of tank emptied by both pipes in 1 minute
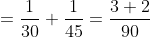
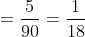
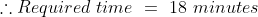
188 Pipe and Cistern - Trick #190
N/A
A tap ‘A’ can fill a tank in ‘x’ hours and ‘B’ can empty the tank in ‘y’ hours.
Then (a) time taken to fill the tank
:x>y)
\&space;time\&space;taken\&space;to\&space;empty\&space;the\&space;tank)
:y>x)
Example-1:
A cistern can be filled with water by a pipe in 5 hours and it can be emptied by a second pipe in 4 hours. If both the pipes are opened when the cistern is full, the time in which it will be emptied is?
Solution:
Here, x = 5, y = 4
hrs)

Example-2:
A tap can fill a cistern in 8 hours and another tap can empty it in 16 hours.
If both the taps are open, the time (in hours) taken to fill the tank will be?
Solution:
Here, x = 8, y = 16
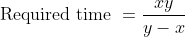

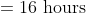
189 Pipe and Cistern - Trick #191
N/A
Two taps A and B can fill a tank in x hours and y hours respectively. If both the pipes are opened together, then the time after which pipe B should be closed so that the tank is full in t hours
![\mathrm{Required\ time\ }=\left[y\left(1-\frac{t}{x}\right)\right]\mathrm{\ hours}](https://latex.codecogs.com/gif.latex?\mathrm{Required\&space;time\&space;}=\left[y\left(1-\frac{t}{x}\right)\right]\mathrm{\&space;hours})
Example-1:
Two pipes X and Y can fill a cistern in 24 minutes and 32 minutes respectively. If both the pipes are opened together, then after how much time (in minutes) should Y be closed so that the tank is full in 18 minutes?
Solution:
x = 24, y = 32, t = 18 Required time
![=\left[y\left(1-\frac{t}{x}\right)\right]\mathrm{\ minutes}](https://latex.codecogs.com/gif.latex?=\left[y\left(1-\frac{t}{x}\right)\right]\mathrm{\&space;minutes})
![=\left[32\left(1-\frac{18}{24}\right)\right]\mathrm{\ minutes}](https://latex.codecogs.com/gif.latex?=\left[32\left(1-\frac{18}{24}\right)\right]\mathrm{\&space;minutes})
![=\left[32\left(1-\frac{3}{4}\right)\right]](https://latex.codecogs.com/gif.latex?=\left[32\left(1-\frac{3}{4}\right)\right])
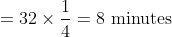
Example-2:
A tap takes 36 hours extra to fill a tank due to a leakage equivalent to half of its inflow. The inflow can fill the tank in how many hours?
Solution:
Here, x = 20, y = 30, t = 18
![\mathrm{Required\ time\ }=\left[x\left(1-\frac{t}{y}\right)\right]](https://latex.codecogs.com/gif.latex?\mathrm{Required\&space;time\&space;}=\left[x\left(1-\frac{t}{y}\right)\right])
![[\therefore\ first\ pipe\ is\ closed]](https://latex.codecogs.com/gif.latex?[\therefore\&space;first\&space;pipe\&space;is\&space;closed])
![=\left[20\left(1-\frac{18}{30}\right)\right]](https://latex.codecogs.com/gif.latex?=\left[20\left(1-\frac{18}{30}\right)\right])
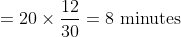
190 Pipe and Cistern - Trick #192
N/A
If pipes A & B can fill a tank in time x, B & C in time y and C & A in time z, then the time required/taken to fill the tank by
\&space;(A+B+C)\&space;together\&space;=\frac{2xyz}{xy+yz+zx})
\&space;A\&space;alone\&space;=\frac{2xyz}{xy+yz-zx})
\&space;B\&space;alone\&space;=\frac{2xyz}{yz+zx-xy})
\&space;C\&space;alone\&space;=\frac{2xyz}{zx+xy-yz})
191 Discount - Trick #193
N/A
If Marked Price = (MP) Selling Price = (SP)
Then, Discount = MP – SP and

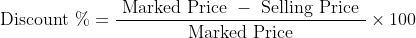
Note: Any kind of Discount is calculated only on marked price and not on selling price or cost price.
Example-1:
An article, which is marked $650, is sold for $572. The discount given is?
Solution:
Here, M.P. = $650
S.P. = $572
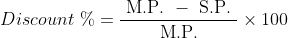
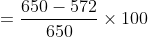
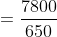
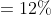
Example-2:
If a dining table with marked price $6,000 was sold to a customer for $5,500, then the rate of discount allowed on the table is?
Solution:
M.P. = $6000
S.P. = $5500
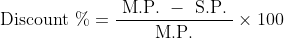
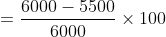
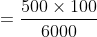
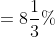
192 Discount - Trick #194
N/A
If article is sold on D% discount, then
}{100})
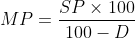
Example-1:
A washing machine is sold at a discount of 30%. If a man buys it for $6,580, its list price is?
Solution:
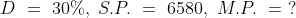

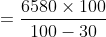
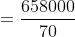
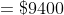
Example-2:
A discount of 14% on the marked price of an article is allowed and then the article is sold for $387. The marked price of the article is?
Solution:
Here, D = 14%, S.P. = $387, M.P. =?

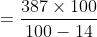

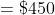
193 Discount - Trick #195
N/A
When successive Discounts 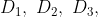 so on, are given then
so on, are given then
\left(\frac{100-D_{2}}{100}\right)\left(\frac{100-D_{3}}{100}\right))
Example-1:
The marked price of an article is $500. It is sold at successive discounts of 20% and 10%. The selling price of the article (in rupees) is?
Solution:
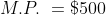
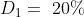
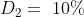
\left(\frac{100-D_2}{100}\right))
\left(\frac{100-10}{100}\right))
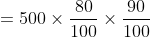
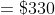
Example-2:
An item is marked for $240 for sale. If two successive discounts of 10% and 5% are allowed on the sale price, the selling price of the article will be?
Solution:
Here, M.P. = $240,
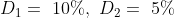
\left(\frac{100-D_2}{100}\right))
\left(\frac{100-5}{100}\right))
194 Discount - Trick #196
N/A
If 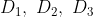 are successive discounts, then equivalent discount/overall discount is (in percentage)
are successive discounts, then equivalent discount/overall discount is (in percentage)
![100-\left[\left(\frac{100-D_1}{100}\right)\left(\frac{100-D_2}{100}\right)\left(\frac{100-D_3}{100}\right)\times100\right]](https://latex.codecogs.com/gif.latex?100-\left[\left(\frac{100-D_1}{100}\right)\left(\frac{100-D_2}{100}\right)\left(\frac{100-D_3}{100}\right)\times100\right])
Example-1:
A single discount equivalent to the successive discounts of 10%, 20% and 25% is?
Solution:
Single equivalent discount
![=100-\left[\left(\frac{100-D_1}{100}\right)\left(\frac{100-D_2}{100}\right)\left(\frac{100-D_3}{100}\right)\times100\right]](https://latex.codecogs.com/gif.latex?=100-\left[\left(\frac{100-D_1}{100}\right)\left(\frac{100-D_2}{100}\right)\left(\frac{100-D_3}{100}\right)\times100\right])
![=100-\left[\left(\frac{100-10}{100}\right)\left(\frac{100-20}{100}\right)\left(\frac{100-25}{100}\right)\times100\right]](https://latex.codecogs.com/gif.latex?=100-\left[\left(\frac{100-10}{100}\right)\left(\frac{100-20}{100}\right)\left(\frac{100-25}{100}\right)\times100\right])
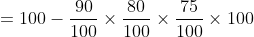
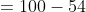
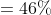
Example-2:
The single discount equal to three consecutive discounts of 10%, 12% and 5% is?
Solution:
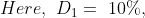
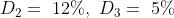
Single equivalent discount
![=100-\left[\left(\frac{100-D_1}{100}\right)\left(\frac{100-D_2}{100}\right)\left(\frac{100-D_3}{100}\right)\times100\right]](https://latex.codecogs.com/gif.latex?=100-\left[\left(\frac{100-D_1}{100}\right)\left(\frac{100-D_2}{100}\right)\left(\frac{100-D_3}{100}\right)\times100\right])
![=100-\left[\left(\frac{100-10}{100}\right)\left(\frac{100-12}{100}\right)\left(\frac{100-5}{100}\right)\times100\right]](https://latex.codecogs.com/gif.latex?=100-\left[\left(\frac{100-10}{100}\right)\left(\frac{100-12}{100}\right)\left(\frac{100-5}{100}\right)\times100\right])
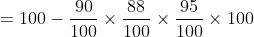
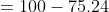

195 Discount - Trick #197
N/A
When two successive discounts are given, then overall discount is %)
Example-1:
Two successive discounts of 5%, 10% are given for an article costing $850.
Present cost of the article is?
Solution:
Single equivalent discount
%=14.5%)
 Cost of article after discount
Cost of article after discount
}{100})
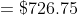
Example-2:
Successive discounts of 10% and 30% are equivalent to a single discount of?
Solution:
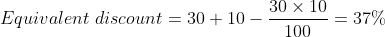
196 Discount - Trick #198
N/A
If r% of profit or loss occur after giving D% discount on marked price, then

(Positive sign for profit and negative for loss)
Example-1:
Jenny allows 4% discount on the marked price of her goods and still earns a profit of 20%. What is the cost price of a TV if its marked price is $850?
Solution:
Here r = 20%, D = 4%, M.P. = $850, C.P. =?
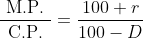
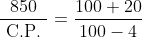
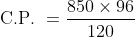
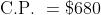
Example-2:
The marked price of an article is $500. A shopkeeper gives a discount of 5% and still makes a profit of 25%. The cost price of the article is.
Solution:
Here, R = 25%, D = 5%, M.P. = 500, C.P. =?
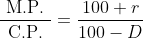
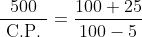
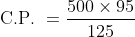
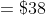
197 Discount - Trick #199
N/A
‘y’ articles (quantity/number) are given free on purchasing ‘x’ articles.
Then,

Example-1:
If a Man purchases 8 articles, he gets 2 articles free of cost. Then find the discount percentage the man gets from his purchase?
Solution:

Here x = 8 and y = 2

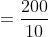
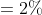
198 Discount - Trick #200
N/A
A tradesman marks his goods r% above his cost price. If he allows his customers a discount of 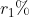 on the marked price. Then is profit or loss percent is
on the marked price. Then is profit or loss percent is
}{100}-r_1)
(Positive sign signifies profit and negative sign signifies loss).
Example-1:
A tradesman marks his goods 10% above his cost price. If he allows his customers 10% discount on the marked price, how much profit or loss does he makes, if any?
Solution:
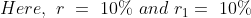
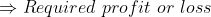
}{100}-r_1)
}{100}-10)

)
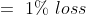
Example-2:
A tradesman marks his goods at 20% above the cost price. He allows his customers a discount of 8% on marked price. Find out his profit per cent.
Solution:
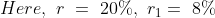
}{100}-r_1)
}{100}-8)
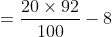
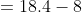

199 Discount - Trick #201
N/A
The marked price of an article is fixed in such a way that after allowing a discount of r% a profit of R% is obtained. Then the marked price of the article is
%\mathrm{\&space;more\&space;than\&space;its\&space;cost\&space;price.})
Example-1:
What price should a shopkeeper mark on an article costing him $200 to gain 35% after allowing a discount of 25%?
Solution:
Here, r = 25%, R = 35%, C.P. = $200
%)
\times100%)
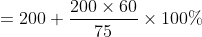
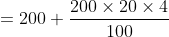
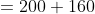
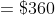
Example-2:
What price should a shopkeeper mark on an article costing him $200 to gain 35% after allowing a discount of 25%?
Solution:
Here, r = 10% R = 20%
}{100-r}\times100%)
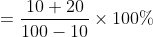
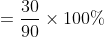

200 Percentages - Formula
N/A
Percentage refers to “Per hundred” i.e., 8% means 8 out of hundred or 8/100. Percentage is denoted by ‘%’.
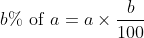
201 Percentages - Trick #202
N/A
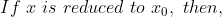
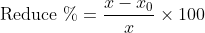
Example:
A reduction in the price of apples enables a person to purchase 3 apples for 1 instead of 1.25. What is the % of reduction in price (approximately)
Solution:
Percentage decrease
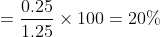
202 Percentages - Trick #203
N/A
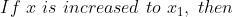
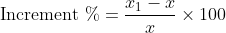
Example:
The price of a commodity rises from $6 per kg to $7.50 per kg. If the expenditure cannot increase, the percentage of reduction in consumption is?
Solution:
Percentage increase
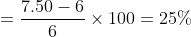
Percentage decrease in consumption
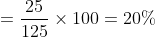
203 Percentages - Trick #204
N/A
If an amount is increased by a% and then it is reduced by a% again, then percentage change will be a decrease of
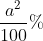
Example:
The salary of a person is decreased by 25% and then the decreased salary is increased by 25%. His new salary in comparison with his original salary?
Solution:
Percentage decrease
^2}{100})
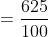
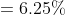
204 Percentages - Trick #205
N/A
If a number is increased by a% and then it is decreased by b%, then resultant change in percentage will be
%)
(Negative for decrease, Positive for increase)
Example:
Water tax is increased by 20% but its consumption is decreased by 20%.
Then the increase or decrease in the expenditure of the money is?
Solution:
Percentage effect
%)
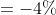
205 Percentages - Trick #206
N/A
If a number is decreased by a% and then it is increased by b%, then net increase or decrease per cent is
%)
(Negative for decrease, Positive for increase)
Example:
The price of an article is reduced by 25% but the daily sale of the article is increased by 30%. The net effect on the daily sale receipts is?
Solution:
Required change
%)
%)
=-2.5%)

206 Percentages - Trick #207
N/A
If a number is first decreased by a% and then by b%, then net decrease percent is
%)
)
Example:
The price of an article was decreased by 10% and again reduced by 10%. By what per cent should the price have been reduced once, in order to produce the same effect as these two successive reductions?
Solution:
A single equivalent reduction to reduction series of x%, y%
%)
%)
%=19%)
207 Percentages - Trick #208
N/A
If a number is first increased by a% and then again increased by b%, then total increase per cent is
%)
Example:
Two successive price increases of 10% and 10% of an article are equivalent to a single price increase of?
Solution:
Single equivalent percentage increase in price
%=21%)
208 Percentages - Trick #209
N/A
If the cost of an article is increased by A%, then how much to decrease the consumption of article, so that expenditure remains same is given by
}\times100\right)%)
Example:
If x is 10% more than y, then by what per cent is y less than x?
Solution:
Required per cent decrease
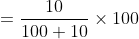
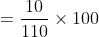
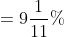
209 Percentages - Trick #210
N/A
If the cost of an article is decreased by A%, then the increase inconsumption of article to maintain the expenditure will be?
}\times100\right)%\mathrm{\&space;(increase)})
Example:
If x is less than y by 25% then y exceeds x by?
Solution:
}\times100%)
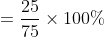

210 Percentages - Trick #211
N/A
If the length of a rectangle is increased by a% and breadth is increased by b%, then the area of rectangle will increase by
%)
Note: If a side is increased, take positive sign and if it is decreased, take negative sign. It is applied for two dimensional figures.
211 Percentages - Trick #212
N/A
If the side of a square is increased by a% then, its area will increase by
%=\left(a+a+\frac{a\cdot&space;a}{100}\right)%)
The above formula is also implemented for circle where radius is used as side. This formula is used for two dimensional geometrical figures having both length and breadth equal.
212 Percentages - Trick #213
N/A
If the side of a square is decreased by a%, then the area of square will decrease by
%)
This formula is also applicable for circles. where decrease % of radius is given.
213 Percentages - Trick #214
N/A
If the length, breadth and height of a cuboid are increased by a%, b% and c% respectively, then,
![Increase%\ in\ volume=\left[a+b+c+\frac{ab+bc+ca}{100}+\frac{abc}{(100)^2}\right]%](https://latex.codecogs.com/gif.latex?Increase%\&space;in\&space;volume=\left[a+b+c+\frac{ab+bc+ca}{100}+\frac{abc}{(100)^2}\right]%)
214 Percentages - Trick #215
N/A
If every side of cube is increased by a%, then increase % in volume
^2}\right)%)
This formula will also be used in calculating increase in volume of sphere. where increase in radius is given.
Example:
If each side of a cube is increased by 10% the volume of the cube will increase by?
Solution:
Increase % in volume
^2}\right)%)
=33.1%)
215 Percentages - Trick #216
N/A
If a% of a certain sum is taken by 1st man and b% of remaining sum is taken by 2nd man and finally c% of remaining sum is taken by 3rd man, then if 'x' rupee is the remaining amount then,
(100-b)(100-c)})
216 Percentages - Trick #217
N/A
If an amount is increased by a% and then again increased by b% and finally increased by c%, So, that resultant amount is ‘x’ rupees, then,
(100+b)(100+c)})
217 Percentages - Trick #218
N/A
If the population/cost of a certain town/ article, is P and annual increment rate is r%, then
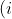\&space;After\&space;\prime\&space;t\&space;\prime\&space;years\&space;population/cost\&space;=P\left(1+\frac{r}{100}\right)^t)
\&space;Before\&space;\prime&space;t\prime\&space;years\&space;population/cost\&space;=\frac{P}{\left(1+\frac{r}{100}\right)^t})
Example:
The present population of a city is 180000. If it increases at the rate of 10% per annum, its population after 2 years will be?
Solution:
Required population after two years
^2)
218 Percentages - Trick #219
N/A
If the population/cost of a town/article is P and it decreases/reduces at the rate of r% annually, then,
\&space;After\&space;\prime\&space;t\&space;\prime\&space;years\&space;population/cost\&space;=P\left(1-\frac{r}{100}\right)^t)
\&space;Before\&space;\prime&space;t\prime\&space;years\&space;population/cost\&space;=\frac{P}{\left(1-\frac{r}{100}\right)^t})
Example:
The value of a commodity depreciates 10% annually. If it was purchased 3 years ago, and its present value is $5,832, what was its purchase price?
Solution:
Let the original price of the article be $x.
According to the question,
^3)
^3)
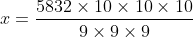
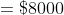
219 Percentages - Trick #220
N/A
On increasing/decreasing the cost of a certain article by x%, a person can buy ‘a’ kg article less/more in ‘y’ rupees, then
\)
a})
[Negative sign when decreasing and positive sign when increasing]
220 Percentages - Trick #221
N/A
If a person saves ‘R’ rupees after spending x% on food, y% on cloth and z% on entertainment of his income then,
}\times&space;R)
Example:
A person gave 20% of his income to his elder son, 30% of the remaining to the younger son and 10% of the balance, he donated to a trust. He is left with $10080. His income was?
Solution:
Here, R = $10080
x = 20%,
y = 30%
and z = 10%
Monthly income
}\times10080)
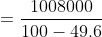
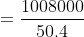
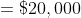
221 Percentages - Trick #222
N/A
The amount of acid/milk is x% in ‘M’ litre mixture. How much water should be mixed in it so that percentage amount of acid/milk would be y%?
}{y})
Example:
8% of the voters in an election did not cast their votes. In this election, there were only two candidates. The winner by obtaining 48% of the total votes defeated his contestant by 1100 votes. The total number of voters in the election was?
Solution:
Here, x = 1100, A = 48
Total number of votes

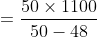
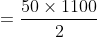
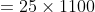
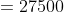
222 Percentages - Trick #223
N/A
An examinee scored m% marks in an exam, and failed by p marks. In the same examination another examinee obtained n% marks and passed with q more marks than minimum, then
}\times(p+q))
Example:
A candidate secured 30% marks in an examination and failed by 6 marks.
Another secured 40% marks and got 6 marks more than the bare minimum to pass. The maximum marks are?
Solution:
Here, m = 30%, n = 40%, p = 6, q = 6.
Maximum Marks
}\times(p+q))
}\times(6+6))
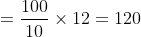
223 Percentages - Trick #224
N/A
In an examination, a% candidates failed in Maths and b% candidates failed in English. If c% candidate failed in both the subjects, then,
\&space;Passed\&space;candidates\&space;in\&space;both\&space;the\&space;subjects\&space;=\&space;100\&space;-&space;(a&space;+&space;b&space;-&space;c)%)
&space;Percentage\&space;of\&space;candidates\&space;who\&space;failed\&space;in\&space;either\&space;subject\&space;=\&space;(a&space;+&space;b&space;-&space;c)%)
Example:
In an examination 34% failed in Mathematics and 42% failed in English. If 20% failed in both the subjects, the percentage of students who passed in both subjects was?
Solution:
a = 34%, b = 42%, c = 20%
Passed candidates in both the subjects
= 100 – (a + b – c)
= 100 – (34 + 42 – 20)
= 100 – 56 = 44%
224 Percentages - Trick #225
N/A
In a certain examination passing marks is a%. If any candidate obtains ‘b’ marks and fails by ‘c’ marks, then,
}{a})
Example:
A student has to secure minimum 35% marks to pass in an examination. If he gets 200 marks and fails by 10 marks, then the maximum marks are
Solution:
a = 35%, b = 200, c = 10
Maximum Marks
}{a})
}{35})
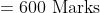
225 Percentages - Trick #226
N/A
In a certain examination, ‘B’ boys and ‘G’ girls participated. b% of boys and g% of girls passed the examination, then,
Percentage of passed students of the total students = %)
Example:
In an examination, there were 1000 boys and 800 girls. 60% of the boys and 50% of the girls passed. Find the percent of the candidates failed?
Solution:
Percentage of passed students
%)
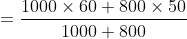
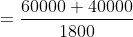
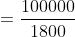
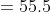
226 Percentages - Trick #227
N/A
If a candidate got A% votes in a poll and he won or defeated by ‘x’ votes, then, what was the total no. of votes which was casted in poll?
})
Example:
In an election there were only two candidates. One of the candidates secured 40% of votes and is defeated by the other candidate by 298 votes.
The total number of votes polled is?
Solution:
Total number of votes
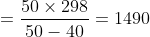
227 Percentages - Trick #228
N/A
If a number ‘a’ is increased or decreased by b%, then the new number will be
\times&space;a)
228 Percentages - Trick #229
N/A
If the present population of a town is P and the population increases or decreases at rate of  in first, second and third year respectively, then
in first, second and third year respectively, then
The population of town after 3 years =
\left(1\pm\frac{R_2}{100}\right)\left(1\pm\frac{R_3}{100}\right))
‘+’ is used when population increases
‘–’ is used when population decreases.
The above formula may be extended for n number of years.
\left(1\pm\frac{R_2}{100}\right)\ldots\ldots\ldots\ldots\ldots\left(1\pm\frac{R_n}{100}\right))
Example:
The value of a machine is 6,250. It decreases by 10% during the first year, 20% during the second year and 30% during the third year. What will be the value of the machine after 3 years?
Solution:
Required price of the machine
\left(1-\frac{20}{100}\right)\left(1-\frac{30}{100}\right))
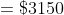
229 Percentages - Trick #230
N/A
If two numbers are respectively x% and y% less than the third number, first number as a percentage of second is
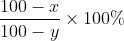
230 Percentages - Trick #231
N/A
If two numbers are respectively x% and y% more than a third number the first as percentage of second is

Example:
Two numbers are respectively 10% and 25% more than a third number.
What per cent is the first of the second?
Solution:
If two numbers are respectively x% and y% more than a third number, the first as a per cent of second is
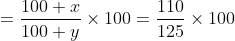

231 Percentages - Trick #232
N/A
If the price of an article is reduced by a% and buyer gets c kg more for some $ b, the new price per kg of article
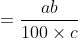
Example-1:
The Government reduced the price of sugar by 10 per cent. By this a consumer can buy 6.2 kg more sugar for $837. The reduced price per kg of sugar is
Solution:
Reduced price per kg
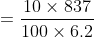

Example-2:
A reduction of 10% in the price of sugar enables a housewife to buy 6.2 kg more for 1116. The reduced price per kg is?
Solution:
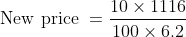
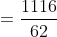
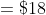
232 Averages - Trick #1
N/A
Average of two or more numbers/quantities is called the mean of these numbers, which is given by
=\frac{\mathrm{\&space;Sum\&space;of\&space;observation\&space;/\&space;quantities\&space;}}{\mathrm{\&space;No.\&space;of\&space;observation\&space;/\&space;quantities\&space;}})

Or
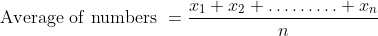
Or
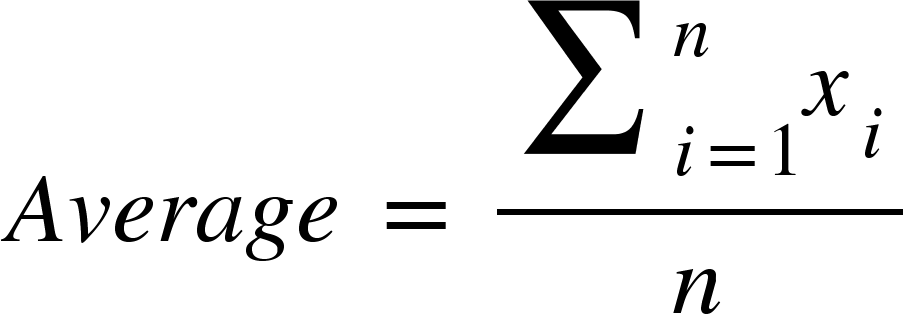
The average of 5 numbers is 6. The average of 3 of them is 8. What is the
average of the remaining two numbers?
Solution:
The average of 5 quantities is 6.
We know that 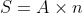
Therefore, the sum of the 5 numbers is 5 × 6 = 30
The average of three of these 5 numbers is 8
Therefore, the sum of these three numbers = 3 × 8 = 24
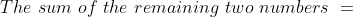
=&space;30\&space;-\&space;24\&space;=\&space;6)
Average of these two remaining numbers = 6/2 = 3
Example 2:
The arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14, x is
12. What is the value of x?
Solution:
As per our Trick (1)

Given that 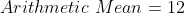
Then
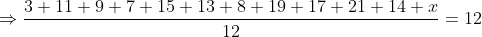

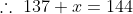
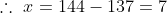
Therefore x = 7.
233 Averages - Trick #2
N/A
If the given observations (x) are occurring with certain frequency (A) then,

where,  are frequencies
are frequencies
Example 1:
The average income of 10 persons is $125 and that of another 5 persons is
$80. The average income of the whole group is?
Solution:
As per our Trick (2)
Average income of whole group

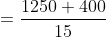
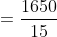
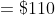
Therefore, average income of the whole group is $110.
Example 2:
A man bought 15 articles at $8 each, 13 at $6 each and 12 at $4 each. The
average price per article is?
Solution:
As per our Trick (2)
Required average price
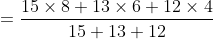
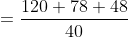
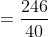
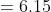
Therefore, average price per article is $6.15.
234 Averages - Trick #3
N/A
The average of ‘n’ consecutive natural numbers starting from 1 to n i.e.
}{2})
Example 1:
The average of the first 100 positive integers is?
Solution:
As per our Trick (3)
}{2})
Average of these numbers
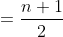
 Required average
Required average
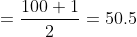
Example 2:
What is the average of all the natural numbers from 49 to 125?
Solution:
As we know,
![Sum\ first\ n\ natural\ numbers\ =\frac{\left[n\left(n+1\right)\right]}{2}](https://latex.codecogs.com/gif.latex?Sum\&space;first\&space;n\&space;natural\&space;numbers\&space;=\frac{\left[n\left(n+1\right)\right]}{2})
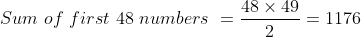
![Sum\ of\ first\ 125\ numbers\ =\frac{\left[125\times126\right]}{2}=7875](https://latex.codecogs.com/gif.latex?Sum\&space;of\&space;first\&space;125\&space;numbers\&space;=\frac{\left[125\times126\right]}{2}=7875)
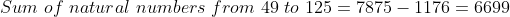

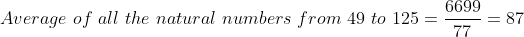
235 Averages - Trick #4
N/A
The average of squares of ‘n’ consecutive natural numbers starting from 1 i.e.
(2n+1)}{6})
Example:
The average of the squares of first ten natural numbers is?
Solution:
As per our Trick (4)
\left(2n+1\right)}{6})
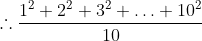
(2\times10+1)}{6})
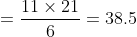
236 Averages - Trick #5
N/A
The average of cubes of first ‘n’ consecutive natural numbers i.e.
^2}{4})
Example:
The average of the cubes of first ten natural numbers is?
Solution:
As per our Trick (5)
^2}{4})

\left(10+1\right)^2}{4})
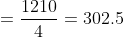
237 Averages - Trick #6
N/A
The average of first ‘n’ consecutive even natural numbers i.e.
)
Example:
The average of the first ten even natural numbers is?
Solution:
Normal Method:
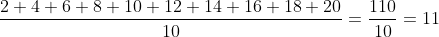
Shortcut Method:
Here, 2n = 10
then n = 10
As per our Trick (6)
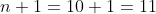
238 Averages - Trick #7
N/A
The average of first ‘n’ consecutive odd natural numbers i.e.
\&space;=n)
Example:
The average of odd numbers up to 100 is?
Solution:
Odd numbers are 1, 3, 5, ............., 99
Total odd numbers are= 50
 Average = 50
Average = 50
239 Averages - Trick #8
N/A
The average of certain consecutive numbers a, b, c, ......... n is 
Example:
The average of odd numbers up to 100 is?
Solution:
Odd numbers are 1, 3, 5, ............., 99
As per our above formula
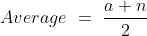
Here a = 1 and n = 99
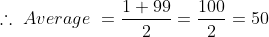
240 Averages - Trick #9
N/A
}{2})
Example:
The average of the first nine integral multiples of 3 is
Solution:
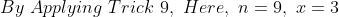
=3\left(\frac{1+9}{2}\right)=15)
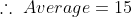
241 Averages - Trick #10
N/A
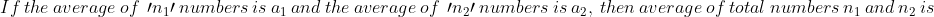
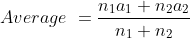
Example-1:
The average of the marks obtained in an examination by 8 students was 51
and by 9 other students was 68. The average marks of all 17 students was?
Solution:
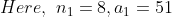
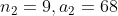

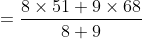
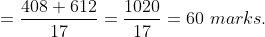
Example-2:
If the average marks of three batches of 55, 60 and 45 students respectively
is 50, 55 and 60, then the average marks of all the students is?
Solution:
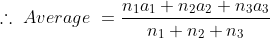
The required average marks
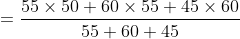
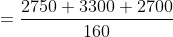
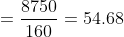
Example-3:

Solution:

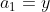

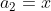
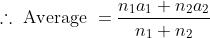
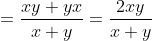
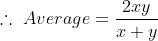
242 Averages - Trick #11
N/A
If the average of m numbers is x and out of these ‘m’ numbers the average of n numbers is y. (or vice versa) then the average of remaining numbers will be
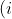\&space;Average\&space;of\&space;remaining\&space;numbers)
)
(ii) Average of remaining numbers
)
Example:
The average of 20 numbers is 15 and the average of first five is 12. The
average of the rest is?
Solution:
Here, m = 20, x = 15 n = 5, y = 12
Then m > n
)
)
)
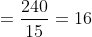
243 Averages - Trick #12
N/A
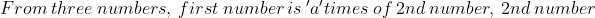
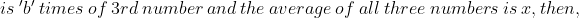
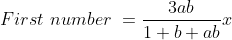
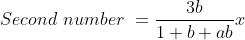
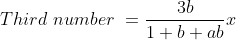
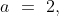
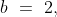
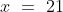

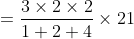
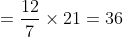
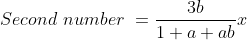
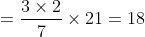
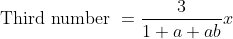
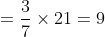
Therefore, least of the numbers are 9.