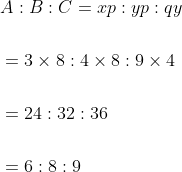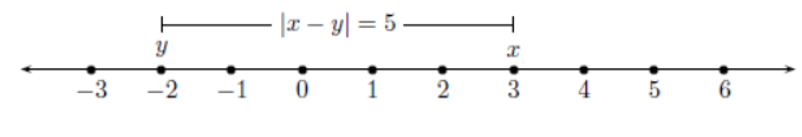1 Averages - Trick #1
N/A
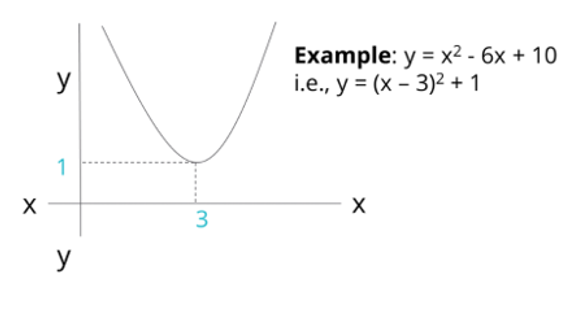
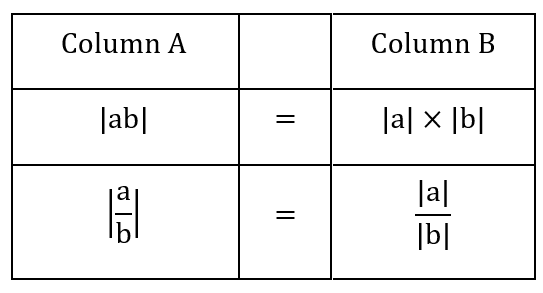
Average of two or more numbers/quantities is called the mean of these numbers, which is given by
=\frac{\mathrm{\&space;Sum\&space;of\&space;observation\&space;/\&space;quantities\&space;}}{\mathrm{\&space;No.\&space;of\&space;observation\&space;/\&space;quantities\&space;}})

Or
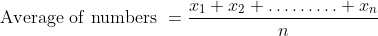
Or
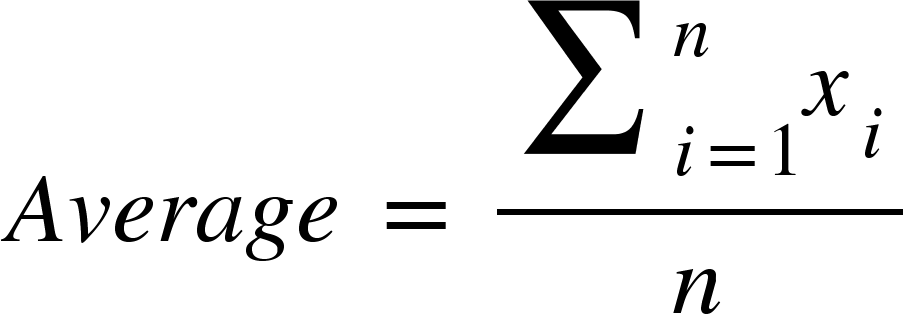
The average of 5 numbers is 6. The average of 3 of them is 8. What is the
average of the remaining two numbers?
Solution:
The average of 5 quantities is 6.
We know that 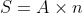
Therefore, the sum of the 5 numbers is 5 × 6 = 30
The average of three of these 5 numbers is 8
Therefore, the sum of these three numbers = 3 × 8 = 24
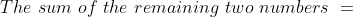
=&space;30\&space;-\&space;24\&space;=\&space;6)
Average of these two remaining numbers = 6/2 = 3
Example 2:
The arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14, x is
12. What is the value of x?
Solution:
As per our Trick (1)

Given that 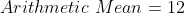
Then
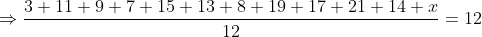

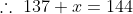
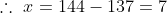
Therefore x = 7.
2 Averages - Trick #2
N/A
If the given observations (x) are occurring with certain frequency (A) then,

where, 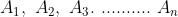 are frequencies
are frequencies
Example 1:
The average income of 10 persons is $125 and that of another 5 persons is
$80. The average income of the whole group is?
Solution:
As per our Trick (2)
Average income of whole group

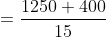
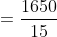
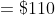
Therefore, average income of the whole group is $110.
Example 2:
A man bought 15 articles at $8 each, 13 at $6 each and 12 at $4 each. The
average price per article is?
Solution:
As per our Trick (2)
Required average price
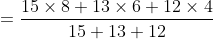
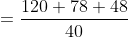
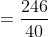
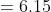
Therefore, average price per article is $6.15.
3 Averages - Trick #3
N/A
The average of ‘n’ consecutive natural numbers starting from 1 to n i.e.
}{2})
Example 1:
The average of the first 100 positive integers is?
Solution:
As per our Trick (3)
}{2})
Average of these numbers
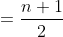
 Required average
Required average
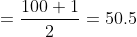
Example 2:
What is the average of all the natural numbers from 49 to 125?
Solution:
As we know,
![Sum\ first\ n\ natural\ numbers\ =\frac{\left[n\left(n+1\right)\right]}{2}](https://latex.codecogs.com/gif.latex?Sum\&space;first\&space;n\&space;natural\&space;numbers\&space;=\frac{\left[n\left(n+1\right)\right]}{2})
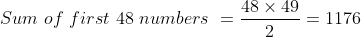
![Sum\ of\ first\ 125\ numbers\ =\frac{\left[125\times126\right]}{2}=7875](https://latex.codecogs.com/gif.latex?Sum\&space;of\&space;first\&space;125\&space;numbers\&space;=\frac{\left[125\times126\right]}{2}=7875)
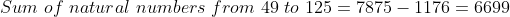

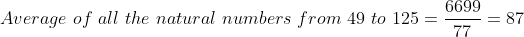
4 Averages - Trick #4
N/A
The average of squares of ‘n’ consecutive natural numbers starting from 1 i.e.
(2n+1)}{6})
Example:
The average of the squares of first ten natural numbers is?
Solution:
As per our Trick (4)
\left(2n+1\right)}{6})
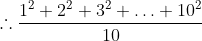
(2\times10+1)}{6})
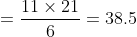
5 Averages - Trick #5
N/A
The average of cubes of first ‘n’ consecutive natural numbers i.e.
^2}{4})
Example:
The average of the cubes of first ten natural numbers is?
Solution:
As per our Trick (5)
^2}{4})

\left(10+1\right)^2}{4})
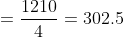
6 Averages - Trick #6
N/A
The average of first ‘n’ consecutive even natural numbers i.e.
)
Example:
The average of the first ten even natural numbers is?
Solution:
Normal Method:
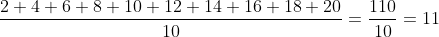
Shortcut Method:
Here, 2n = 10
then n = 10
As per our Trick (6)
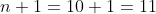
7 Averages - Trick #7
N/A
The average of first ‘n’ consecutive odd natural numbers i.e.
\&space;=n)
Example:
The average of odd numbers up to 100 is?
Solution:
Odd numbers are 1, 3, 5, ............., 99
Total odd numbers are= 50
 Average = 50
Average = 50
8 Averages - Trick #8
N/A
The average of certain consecutive numbers a, b, c, ......... n is 
Example:
The average of odd numbers up to 100 is?
Solution:
Odd numbers are 1, 3, 5, ............., 99
As per our above formula
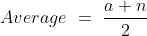
Here a = 1 and n = 99
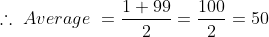
9 Averages - Trick #9
N/A
}{2})
Example:
The average of the first nine integral multiples of 3 is
Solution:
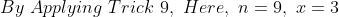
=3\left(\frac{1+9}{2}\right)=15)
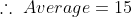
10 Averages - Trick #10
N/A
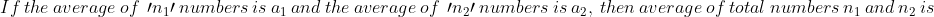
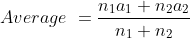
Example-1:
The average of the marks obtained in an examination by 8 students was 51
and by 9 other students was 68. The average marks of all 17 students was?
Solution:
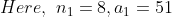
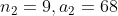

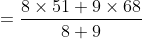
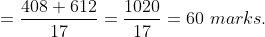
Example-2:
If the average marks of three batches of 55, 60 and 45 students respectively
is 50, 55 and 60, then the average marks of all the students is?
Solution:
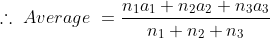
The required average marks
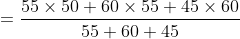
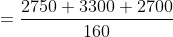
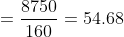
Example-3:

Solution:
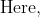

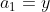

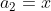
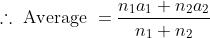
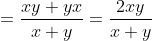
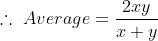
11 Averages - Trick #11
N/A
If the average of m numbers is x and out of these ‘m’ numbers the average of n numbers is y. (or vice versa) then the average of remaining numbers will be
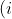\&space;Average\&space;of\&space;remaining\&space;numbers)
)
(ii) Average of remaining numbers
)
Example:
The average of 20 numbers is 15 and the average of first five is 12. The
average of the rest is?
Solution:
Here, m = 20, x = 15 n = 5, y = 12
Then m > n
)
)
)
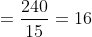
12 Averages - Trick #12
N/A
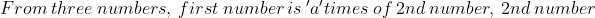
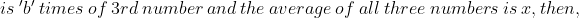
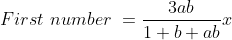
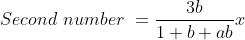
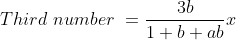
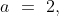
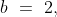
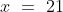

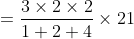
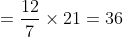
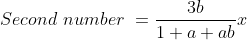
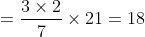
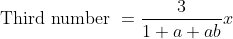
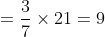
Therefore, least of the numbers are 9.
13 Averages - Trick #13
N/A
\&space;numbers,\&space;the\&space;average\&space;of\&space;first\&space;n\&space;numbers\&space;is\&space;'F'&space;and\&space;the)
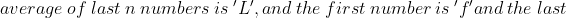
)
Example:
Out of four numbers the average of the first three is 16 and that of the last three is 15. If the last number is 20 then the first number is?
Solution:
Normal Method:
\&space;Let\&space;three\&space;numbers\&space;be\&space;a,b\&space;and\&space;c\&space;respectively.\)
\)
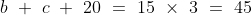
)
\&space;-\&space;(ii),\)
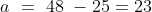
Shortcut Method:
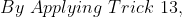
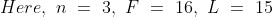
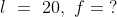
)
)
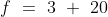
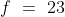
14 Averages - Trick #14
N/A
If in the group of N persons, a new person comes at the place of a person of ‘T’ years, so that average age, increases by ‘t’ years
Then, the age of the new person = T + N.t
If the average age decreases by ‘t’ years after entry of new person, then the age of the new person = T – N.t
Example:
3 years ago, the average age of a family of 5 members was 17 years. A baby having been born, the average age of the family is the same today. The present age of the baby is?
Solution:
Normal Method:
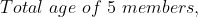
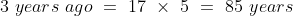
=100\&space;years\)

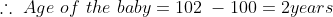
Shortcut Method:
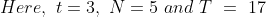
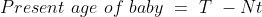
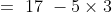
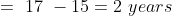
15 Averages - Trick #15
N/A
The average age of a group of N students is ‘T’ years. If ‘n’ students join, the average age of the group increases by ‘t’ years, then average age of new students
t)
If the average age of the group decreases by ‘t’ years, then average age of new students
t)
Example-1:
The mean of 9 observations is 16. One more observation is included and
the new mean becomes 17. The 10th observation is?
Solution:
Normal Method:
Sum of Ten observations – Sum of nine observations = Tenth observation
 Tenth observation = 10 × 17 – 16 × 9 = 170 – 144 = 26
Tenth observation = 10 × 17 – 16 × 9 = 170 – 144 = 26
Shortcut Method:
By Applying Trick 15,
Here, N = 9, T = 16 n = 1, t = 1
t)
\times1)

Example-2:
The average of 100 numbers is 44. The average of these 100 numbers and 4
other new numbers are 50. The average of the four new numbers will be?
Solution:
By Applying Trick 15,
Here, N = 100, T = 44, n = 4, t = 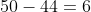
t)
\times6)
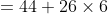

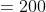

16 Averages - Trick #16
N/A
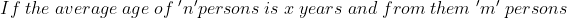
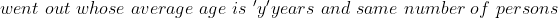
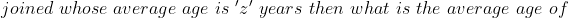
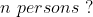
}{n}\right\}\mathrm{\&space;years})
Example:
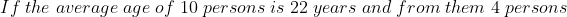
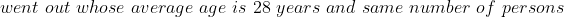
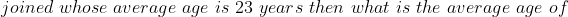
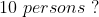
Solution:
By Applying Trick 16,
Here, n = 10, m = 4, x = 22, y= 28 and z = 23
}{n})
}{10}\right))
}{10}\right))
)
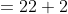
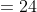
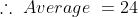
17 Averages - Trick #17
N/A
If in a group, one member is replaced by a new member, then, \&space;\pm\&space;xn)
\&space;or\&space;decrease\&space;(-)&space;in&space;average)
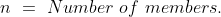
Example-1:
The average weight of 8 persons increases by 2.5 kg when a new person
comes in place of one of them weighing 65 kg. The weight of the new
person is?
Solution:
By Applying 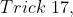
Here, x = 2.5, n = 8
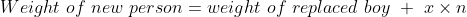
)
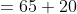
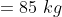
Example-2:
In a class, there are 40 boys and their average age is 16 years. One boy, aged 17 years, leaving the class and another joining, the average age becomes 15.875 years. The age of the new boy is?
Solution:

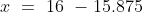
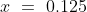
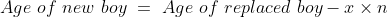
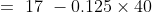
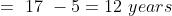
Example-3:
In a class there are 30 boys and their average age is 17 years. On one boy aged 18 years leaving the class and another joining, the average age becomes 16.9 years. The age of new boy is?
Solution:
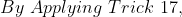
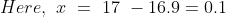
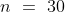
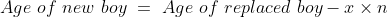

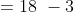
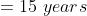
18 Averages - Trick #18
N/A
\&space;of\&space;added\)
\pm\&space;x\&space;(n\&space;+\&space;1))
\&space;or\&space;decrease\&space;(-)&space;in\&space;average\&space;age\&space;(or\&space;income))
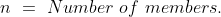
Example-1:
Average weight of 25 students of a class is 50 kg. If the weight of the class teacher is included, the average is increased by 1 kg. The weight of the teacher is?
Solution:
By Applying Trick 18,
Here, Average = 50,
n = 25,
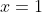
\)
= 50 + 1 (25 + 1)
= 50 + 26
= 76 kg
Example-2:
The mean weight of 34 students of a school is 42 kg. If the weight of the teacher be included, the mean rises by 400 grams. Find the weight of the teacher (in kg)?
Solution:
By Applying Trick 18,
Here, Average = 42,
n = 34,
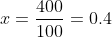
\)
= 42 + 0.4 (34 + 1)
= 42+ 14
= 56 kg
The average age of four brothers is 12 years. If the age of their mother is also included, the average is increased by 5 years. The age of the mother (in years) is?
Solution:
By Applying Trick 18,
Here, Average = 12,
x = 5, n = 4
Age of mother = Average + x (n+1)
= 12 + 5 (4 + 1)
= 12 + 25
= 37 years
19 Averages - Trick #19
N/A
If a member leaves the group, then income (or age) of left member = \&space;\pm\&space;x\&space;(n\&space;-&space;1))
where, x = increase (+) or decrease (–) in average income (or age) n = Number of members.
Example:
The average of five numbers is 140. If one number is excluded, the average of the remaining four numbers is 130. The excluded number is?
Solution:
By Applying Trick 19,
Here, Average = 140,
x = (140 – 130) = 10
n = 5
Excluded number = Average + x (n – 1)
= 140 + 10 × 4
= 180
20 Averages - Trick #20
N/A
If average of n numbers is m later on it was found that a number ‘a’ was misread as ‘b’.
}{n})
Example-1:
The average of a collection of 20 measurements was calculated to be 56 cm.
But later it was found that a mistake had occurred in one of the measurements which was recorded as 64 cm., but should have been 61 cm.
The correct average must be
Solution:
By Applying Trick 20,
Here, n = 20, m = 56
a = 61, b = 64
}{n})
)
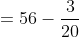
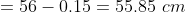
Example-2:
The average marks of 100 students were found to be 40. Later on, it was discovered that a score of 53 was misread as 83. Find the correct average corresponding to the correct score.
Solution:
By Applying Trick 20,
Here, n = 100, m = 40
a = 53, b = 83
}{n})
)
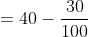
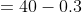
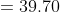
Example-3:
The average weight of a group of 20 boys was calculated to be 89.4 kg and it was later discovered that one weight was misread as 78 kg instead of 87kg. The correct average weight is?
Solution:
By Applying Trick 20,
Here, n = 20, m = 89.4
a = 87, b = 78
}{n})
)
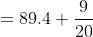
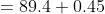
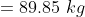
21 Averages - Trick #21
N/A
If the average of n numbers is m later on it was found that two numbers a and b misread as p and q.
}{n})
Example-1:
The mean of 50 numbers is 30. Later it was discovered that two entries were wrongly entered as 82 and 13 instead of 28 and 31. Find the correct mean.
Solution:
By Applying Trick 21,
Here, n = 50, m = 30
a = 28, b = 31
p = 82, q = 13
}{n})
}{50})
)
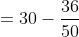
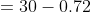
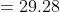
Example-2:
The average of marks of 14 student was calculated as 71. But it was later found that the marks of one student had been wrongly entered as 42 instead of 56 and of another as 74 instead of 32. The correct average is?
Solution:
By Applying Trick 21,
Here, n = 14, m = 71
a = 56, b = 42
p = 32, q = 74
}{n})
}{50})
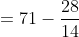
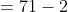

Example-3:
Mean of 10 numbers is 30. Later on, it was observed that numbers 15, 23 are wrongly taken as 51, 32. The correct mean is?
Solution:
By Applying Trick 21,
Here, n = 10, m = 30
a = 15, b = 23
p = 51, q = 32
}{n})
}{10})
)
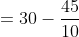
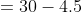
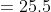
22 LCM and HCF - Trick #22
N/A
Least common Multiple (L.C.M):
The least number which is divisible by two or more given numbers, that least number is called L.C.M. of the numbers.
Ex: L.C.M. of 3,5,6 is 30, because all 3 numbers divide 30, 60, 90, ...... and soon perfectly and 30 is minimum of them.
Highest Common Factor (H.C.F):
It is also called Greatest common Divisor (G.C.D). When a greatest number divides perfectly the two or more given numbers then that number is called the H.C.F. of two or more given numbers.
Ex: The H.C.F of 10, 20, 30 is 10 as they are perfectly divided by 10,5 and 2 and 10 is highest or greatest of them.
Factor and Multiple:
If a number m, divides perfectly second number n, then m is called the factor of n and n is called the multiple of m.
Trick #22
Finding LCM by Large Number method:
Case - 1:
LCM of 6, 12, 24, 48
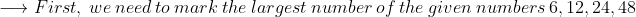
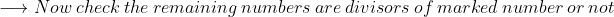
In this case remaining numbers 6, 12, 24 are divisors of 48 then the LCM of the numbers is 48.
Case - 2:
LCM of 5, 10, 20, 50
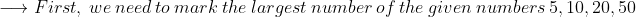
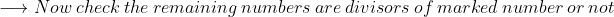
In this case only 5, 10 are divisors of 50 then eliminate 5, 10 from the list. 20, 50
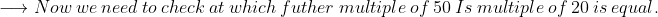

Note: If there is no common factor between two numbers, then L.C.M. will be the product of both numbers.
100 is the common multiple. Then the LCM of the numbers is 100.
Case - 3:
LCM of 8, 16, 19, 32

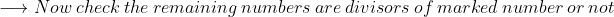
In this case only 8, 16 are divisors of 32 then eliminate 8, 16 from the list.19, 32
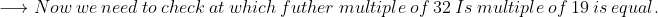
But 19 is prime then the LCM becomes
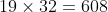
Then the LCM of the numbers is 608.
Example-1:
Find the LCM of the numbers 7, 14, 35, 70
Solution:
By Applying our case – 1 we can directly say the LCM is 70 as all the remaining numbers are divisors of highest number 70.
Example-2:
Find the LCM of the numbers 3, 9, 27, 63
Solution:
By Applying our case – 2 we can directly say the LCM is 189 as 9, 18 are divisors of highest number 72 and 189 is common least multiple of remaining numbers 27 and 63.
Therefore LCM = 189.
Example-3:
Find the LCM of the numbers 8, 11, 32, 64
Solution:
By Applying our case – 3 we can directly say the LCM is 704 as 8, 32 are divisors of highest number 64 and 11 is the prime number.
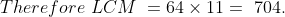
23 LCM and HCF - Trick #23
N/A
Finding HCF By Applying minimum difference method:
Case - 1:
HCF of 6, 12, 18
 If the difference between the numbers are same then we need to consider the common difference.
If the difference between the numbers are same then we need to consider the common difference.
In this case the common difference is 6.
Note: If the common difference is a prime number then the HCF will be the prime number if that prime number is divisible by all of the given numbers else HCF will be ‘1’.
Else
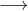 we need to prime factorize the difference.
we need to prime factorize the difference.
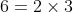
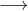 Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Divide 6, 12, 18 by 2 we get 3, 6, 9
Now divide 3, 6, 9 by 3 we get 1 2, 3
Therefore, qualified factors are 2, 3
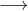 Now multiply the factors
Now multiply the factors
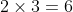
Therefore HCF = 6
Case - 2:
HCF of 12, 42, 66
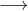 If the difference between the numbers are not same then we need to consider the minimum difference among them.
If the difference between the numbers are not same then we need to consider the minimum difference among them.
In this case
Difference from 12 to 42 = 30
Difference from 42 to 66 = 24
Difference from 12 to 66 = 54
Therefore, the minimum(least) difference is 24
Note: If the minimum difference is a prime number then the HCF will be the prime number if that prime number is divisible by all of the given numbers else HCF will be ‘1’.
Else
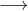 Now we need to prime factorize the minimum difference.
Now we need to prime factorize the minimum difference.
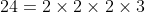
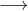 Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Now we need to divide each factor with all of the given numbers and need select the factors which are qualified in the below division method.
Divide 30, 24, 54 by 2 we get 15, 12, 18
Clearly remaining 2’s will not divide 15.
So now we need to check 3
Now divide 15, 12, 18 by 3 we get 5, 4, 6
Therefore, qualified factors are 2, 3
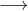 Now multiply the factors
Now multiply the factors
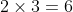
Therefore HCF = 6
Example-1:
Find the HCF of the numbers 7, 14, 21, 28
Solution:
By Applying our case – 1
The common difference is 7 and it is the prime number and divisible by all of the given numbers
Therefore HCF = 7
Example-2:
Find the HCF of the numbers 12, 30, 84, 102
Solution:
By Applying our case – 2
The minimum difference is 18 and it is not the prime number
Then prime factorization of 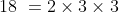
Divide 12, 30, 84, 102 by 2 we get 6, 15, 42, 51
Now divide 6, 15, 42, 51 by 3 we get 2, 5, 14, 17
But remaining 3 will not divide 2, 5, 14, 17
Then factors which are divisible by all of the given numbers are 2, 3
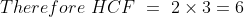
Example-3:
Find the HCF of the numbers 27, 32, 37, 42
Solution:
By Applying our case – 1
The common difference is 5 and it is the prime number but it is not divisible by all of the given numbers
Therefore HCF = 1
24 LCM and HCF - Trick #24
N/A
If we have LCM and HCF of two numbers then
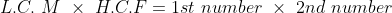
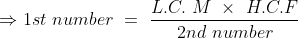
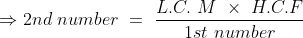
Example-1:
The LCM of two numbers is 864 and their HCF is 144. If one of the numbers are 288, the other number is?
Solution:
By Applying Trick 23,
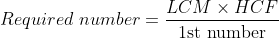


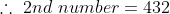
Example-2:
The product of two numbers is 1280 and their H.C.F. is 8. The L.C.M. of the numbers will be?
Solution:
By Applying Trick 23,
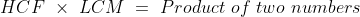
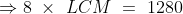
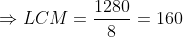
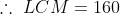
Example-3:
The product of two numbers is 4107 and their L.C.M. is 111. The H.C.F. of the numbers will be?
Solution:
By Applying Trick 23,
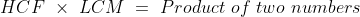

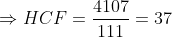
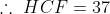
25 LCM and HCF - Trick #24
N/A
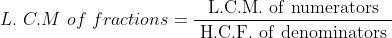
Example-1:
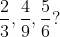
Solution:
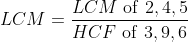
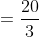
Example-2:
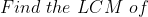
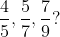
Solution:
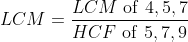

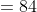
Example-3:
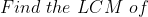
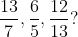
Solution:
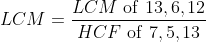
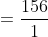
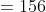
26 LCM and HCF - Trick #25
N/A
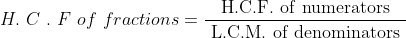
Example-1:
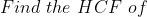
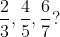
Solution:
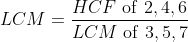
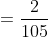
Example-2:
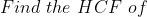
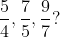
Solution:
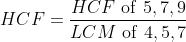

Example-3:
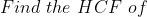
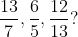
Solution:

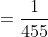
27 LCM and HCF - Trick #26
N/A
When a number is divided by a, b or c leaving same remainder ‘r’ in each case then that number must be k + r where k is LCM of a, b and c.
Example-1:
The least number which when divided by 4, 6, 8, 12 and 16 leaves a remainder of 2 in each case is?
Solution:
By Applying Trick 26,
L.C.M. of 4, 6, 8, 12 and 16 = 48
 Required number = 48 + 2 = 50
Required number = 48 + 2 = 50
Example-2:
Find the least number which when divided separately by 15, 20, 36 and 48 leaves 3 as remainder in each case?
Solution:
By Applying Trick 26,
Required number = (LCM of 15, 20, 36 and 48) + 3
 LCM = 2 × 2 × 3 × 5 × 3 × 4 = 720
LCM = 2 × 2 × 3 × 5 × 3 × 4 = 720
 Required number = 720 + 3 = 723
Required number = 720 + 3 = 723
Example-3:
The least number, which when divided by 12, 15, 20 or 54 leaves a remainder of 4 in each case, is?
Solution:
By Applying Trick 26,
LCM of 15, 12, 20, 54 = 540
 Required number = 540 + 4 = 544
Required number = 540 + 4 = 544
28 LCM and HCF - Trick #27
N/A
When a number is divided by a, b or c leaving remainders p, q or r respectively such that the difference between divisor and remainder in each case is same i.e., (a – p) = (b – q) = (c – r) = t (say) then that (least) number must be in the form of (k – t), where k is LCM of a, b and c.
Example-1:
The least number, which when divided by 4, 5 and 6 leaves remainder 1, 2 and 3 respectively, is?
Solution:
By Applying Trick 27,
Here 4 – 1 = 3,
5 – 2 = 3,
6 – 3 = 3
 The required number = LCM of (4, 5, 6) – 3 = 60 – 3 = 57
The required number = LCM of (4, 5, 6) – 3 = 60 – 3 = 57
Example-2:
The smallest number, which when divided by 12 and 16 leaves remainder 5 and 9 respectively, is?
Solution:
By Applying Trick 27,
Here, 12 – 5 = 7,
16 – 9 = 7
 Required number = (L.C.M. of 12 and 16) – 7 = 48 – 7 = 41
Required number = (L.C.M. of 12 and 16) – 7 = 48 – 7 = 41
Example-3:
When a number is divided by 15, 20 or 35, each time the remainder is 8.
Then the smallest number is?
Solution:
LCM of 15, 20 and 35 = 420
 Required least number = 420 + 8 = 428
Required least number = 420 + 8 = 428
29 LCM and HCF - Trick #28
N/A
The largest number which when divide the numbers a, b and c the remainders are same then that largest number is given by H.C.F. of (a – b), (b – c) and (c – a).
Example:
The greatest number, which when divide 24, 30 and 48 leave same remainder is?
Solution:
,(30-48)&space;and&space;(48&space;-24))
= HCF of 6, 18 and 24
 HCF = 2
HCF = 2
30 LCM and HCF - Trick #29
N/A
The largest number which when divide the numbers a, b and c give remainders as p, q, r respectively is given by H.C.F. of (a – p), (b – q) and (c – r).
Example-1:
The greatest number, which when divide 989 and 1327 leave remainders 5 and 7 respectively, is?
Solution:
Required number = HCF of (989 – 5) and (1327 – 7)
= HCF of 984 and 1320 = 24
 HCF = 24
HCF = 24
Example-2:
What is the greatest number that will divide 307 and 330 leaving remainders 3 and 7 respectively?
Solution:
Required number = HCF of (307 – 3) and (330 – 7)
= HCF of 304 and 323 = 19
 HCF = 19
HCF = 19
Example-3:
Which greatest number will divide 3026 and 5053 leaving remainders 11 and 13 respectively?
Solution:
Required number = HCF of (3026 – 11) and (5053 – 13)
= HCF of 3015 and 5040 = 45
 HCF = 45
HCF = 45
31 LCM and HCF - Trick #30
N/A
Greatest n digit number which when divided by three numbers p, q, r leaves no remainder will be
Required Number = (n – digit greatest number) – R
R is the remainder obtained on dividing greatest n digit number by L.C.M of p, q, r.
Example-1:
The largest 4-digit number exactly divisible by each of 12, 15, 18 and 27 is?
Solution:
The largest number of 4-digits is 9999.
L.C.M. of divisors 12, 15, 18 and 27
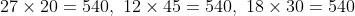
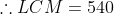
Divide 9999 by 540, now we get 279 as remainder. 9999 – 279 = 9720
Hence, 9720 is the largest 4-digit number exactly divisible by each of 12,
15, 18 and 27.
Example-2:
The greatest 4-digit number exactly divisible by 10, 15, 20 is?
Solution:
LCM of 10, 15 and 20 = 60
Largest 4-digit number = 9999
Divide 9999 by 60, now we get 39 as remainder. 9999 – 39 = 9960
Hence, 9960 is the largest 4-digit number exactly divisible by each of 10, 15 and 20.
32 LCM and HCF - Trick #31
N/A
The n digit largest number which when divided by p, q, r leaves remainder ‘a’ will be
Required number = [n – digit largest number – R] + a
where, R is the remainder obtained when n – digit largest number is divided by the L.C.M of p, q, r.
Example:
The largest number of five digits which, when divided by 16, 24, 30, or 36 leaves the same remainder 10 in each case, is?
Solution:
We will find the LCM of 16, 24, 30 and 36.
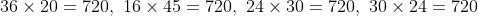
The largest number of five digits = 99999
On dividing 99999 by 720, the remainder = 639
 The largest five-digit number divisible by 720 = 99999 – 639 = 99360
The largest five-digit number divisible by 720 = 99999 – 639 = 99360
 Required number = 99360 + 10 = 99370
Required number = 99360 + 10 = 99370
33 Time and Distance - Trick #32
N/A
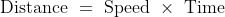
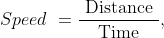
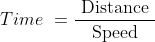
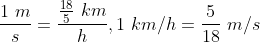
Example-1:
A train is travelling at the rate of 45km/hr. How many seconds it will take to cover a distance of 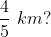
Solution:
By Applying Trick 32,
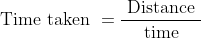
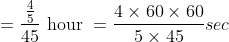

Example-2:
An aeroplane covers a certain distance at a speed of 240 km hour in 5 hours. To cover the same distance in 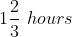 it must travel at a speed of?
it must travel at a speed of?
Solution:
By Applying Trick 32,
Let the required speed is x km/ hr
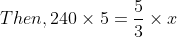
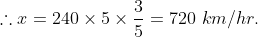
Example-3:
A man walking at the rate of 5 km/hr. crosses a bridge in 15 minutes. The length of the bridge (in metres) is?
Solution:
By Applying Trick 32,
Speed of the man = 5km/hr
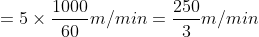
Time taken to cross the bridge
= 15 minutes Length of the bridge
= speed × time
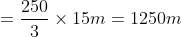
34 Time and Distance - Trick #33
N/A
If a man travels different distances 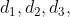 ....... and so on in different time
....... and so on in different time 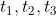 respectively then,
respectively then,
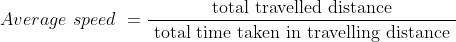
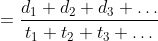
Example-1:
A man travels a distance of 24 km at 6 kmph. Another distance of 24 km at 8 kmph and a third distance of 24 km at 12 kmph. His average speed for the whole journey (in kmph) is?
Solution:
By Applying Trick 33,
Total distance = 24 + 24 + 24 = 72 km.
\mathrm{\&space;hours\&space;}=\&space;\left(4+3+2\right)\&space;hours=9\&space;hours\)
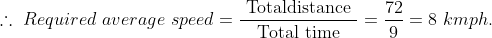
Example-2:
P travels for 6 hours at the rate of 5 km/hour and for 3 hours at the rate of 6 km/hour. The average speed of the journey in km/hour is?
Solution:
By Applying Trick 33,
Total distance = 5 × 6 + 3 × 6 = 30 + 18 = 48 km
Total time = 9 hours
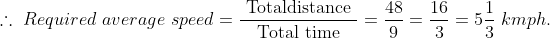
Example-3:
A train travelled at a speed of 35 km/hr for the first 10 minutes and at a speed of 20 km/hr for the next 5 minutes. The average speed of the train for the total 15 minutes is?
Solution:
By Applying Trick 33,
km\)
=\frac{45}{6}\mathrm{\&space;}km\)
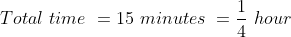
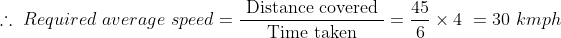
35 Time and Distance - Trick #34
N/A
If a man travels different distances 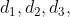 and so on with different speeds
and so on with different speeds 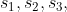 respectively then,
respectively then,
+\left(\frac{d_2}{s_2}\right)+\left(\frac{d_3}{s_3}\right)+\ldots})
Example:
A man travels a distance of 24 km at 6 kmph. Another distance of 24 km at 8 kmph and a third distance of 24 km at 12 kmph. His average speed for the whole journey (in kmph) is?
Solution:
By Applying Trick 34,
Total distance = 24 + 24 + 24 = 72 km.
\mathrm{\&space;hours\&space;}=\&space;\left(4+3+2\right)\&space;hours=9\&space;hours\)
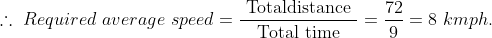
36 Time and Distance - Trick #35
N/A
If a distance is divided into “n” equal parts each travelled with different speeds, then,
})
where n = number of equal parts
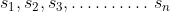 are speeds
are speeds
Example:
Four men travelled a distance which is divided into 4 equal parts with
speeds 5 kmph, 10 kmph, 15 kmph and 20 kmph then average speed?
Solution:
By Applying Trick 35,
Given that 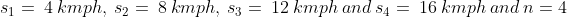
}\&space;=\frac{4}{\left(\frac{1}{5}+\frac{1}{10}+\frac{1}{15}+\frac{1}{20}\right)})
})
})
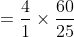
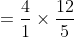
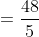
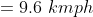
37 Time and Distance - Trick #36
N/A
If a bus travels from A to B with the speed x km/h and returns from B to A with the speed y km/h, then,
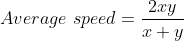
Example-1:
Jackson with his family travelled from Texas to New York by car at a speed of 40 km/hr and returned to Texas at a speed of 50 km/hr. The average speed for the whole journey is?
Solution:
By Applying Trick 36,
\&space;kmph)
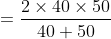
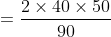
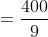
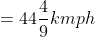
Example-2:
A boy goes to his school from his house at a speed of 3 km/hr and returns at a speed of 2 km/hr. If he takes 5 hours in going and coming, the distance between his house and school is?
Solution:
By Applying Trick 36,
Here, x = 3, y = 2
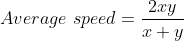
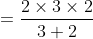
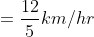
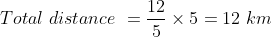

Example-3:
A boy goes to his school from his house at a speed of 3 km/hr and returns at a speed of 2 km/hr. If he takes 5 hours in going and coming, the distance between his house and school is?
Solution:
By Applying Trick 36,
Here, x = 25, y = 4
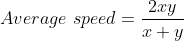
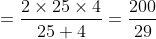

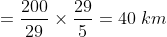
38 Time and Distance - Trick #37
N/A
If 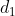 distance is travelled in
distance is travelled in 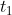 time and
time and 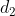 distance is travelled in
distance is travelled in 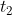 time then,
time then,

![\Rightarrow Distance\ \propto\ time\ [provided\ speed\ is\ constant]](https://latex.codecogs.com/gif.latex?\Rightarrow&space;Distance\&space;\propto\&space;time\&space;[provided\&space;speed\&space;is\&space;constant])
Example:
A man travelled 10 km in 2hrs and x km in 4hrs then find the value of x ?
Solution:
By Applying Trick 37,

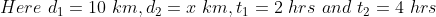
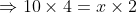
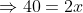
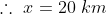
39 Time and Distance - Trick #38
N/A
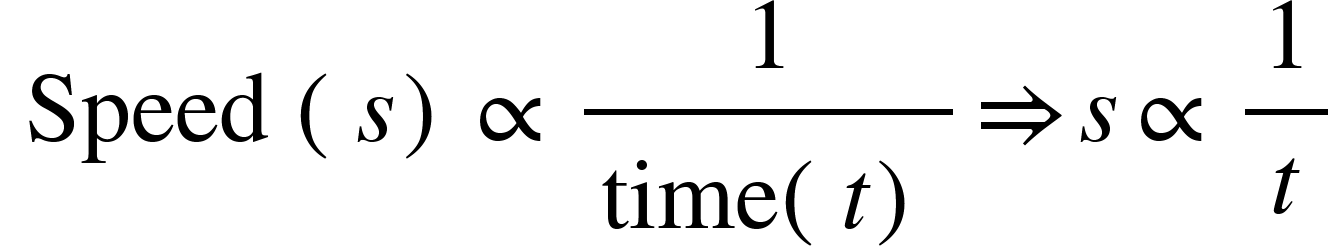
![\therefore{\ }s_1t_1=s_2t_2\ [provided\ distance\ is\ constant]](https://latex.codecogs.com/gif.latex?\therefore{\&space;}s_1t_1=s_2t_2\&space;[provided\&space;distance\&space;is\&space;constant])
Example:
A man travelled a distance of 24 km in 2hrs at what speed he needs to travel the same distance in 1.5 hrs?
Solution:
By Applying Trick 38,
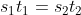
Here
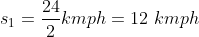
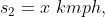
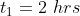
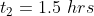
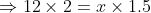
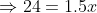
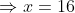
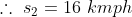
40 Time and Distance - Trick #39
N/A
If an object increases/decreases its speed from x km / hr to y km / hr to cover a distance in 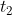 hours in place of
hours in place of 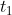 hours then
hours then
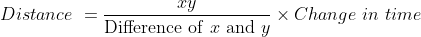
Or
\times&space;Change\&space;in\&space;time)
Example:
A Truck increases its speed from 45 kmph to 60 kmph in order to cover the distance in 6 hrs to deliver the goods 2 hrs earlier than expected time. Find the distance of the journey?
Solution:
By Applying Trick 39,
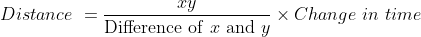
Or
)
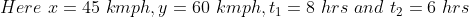
)


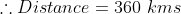
41 Time and Distance - Trick #40
N/A
If an object travels certain distance with the speed of A/B of its original speed and reaches its destination ‘t’ hours before or after, then the taken time by object travelling at original speed is
}\times\mathrm{\&space;time\&space;}(\mathrm{\&space;in\&space;hour\&space;}))
Example:
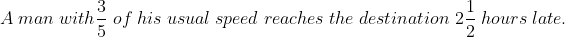
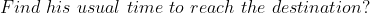
Solution:
By Applying Trick 40,
}\times\mathrm{\&space;time\&space;}(\mathrm{\&space;in\&space;hour\&space;}))
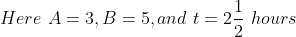
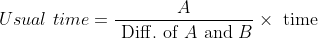
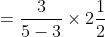
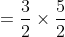
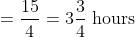
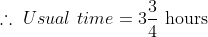
42 Time and Distance - Trick #41
N/A
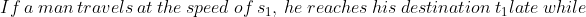
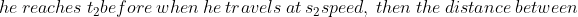
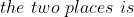
\times\left(t_1+t_2\right)}{s_2-s_1})
Example-1:
You arrive at your school 5 minutes late if you walk with a speed of 4 kmph,but you arrive 10 minutes before the scheduled time if you walk with a speed of 5 kmph. The distance of your school from your house (in km) is?
Solution:
By Applying Trick 41,
\left(t_1+t_2\right)}{s_2-s_1})
Here
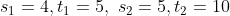
(5+10)}{5-4})
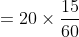
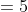

Example-2:
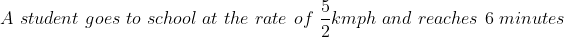
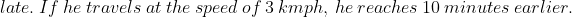

Solution:
By Applying Trick 41,
\left(t_1+t_2\right)}{s_2-s_1})
Here,
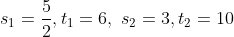
(6+10)}{3-\frac{5}{2}})
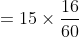
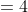
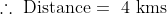
Example-3:

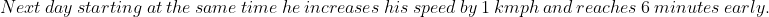
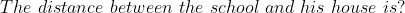
Solution:
By Applying Trick 41,
\left(t_1+t_2\right)}{s_2-s_1})
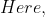
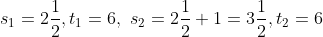
(6+6)}{\frac{7}{2}-\frac{5}{2}})
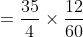
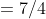

43 Time and Distance - Trick #42
N/A
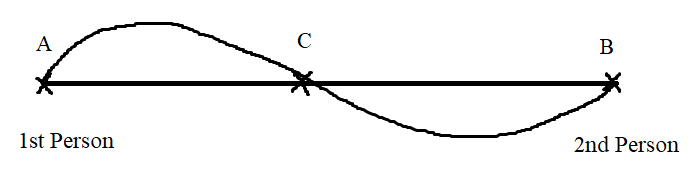
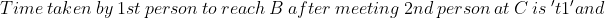

}{\mathrm{\&space;Speed\&space;of\&space;}2nd\&space;person\left(s_2\right)}=\sqrt{\frac{t_2}{t_1}})
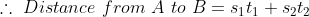
Example-1:
Two trains X and Y start from City 1 to City 2 and from City 2 to City 1 respectively. After passing each other they take 4 hours 48 minutes and 3 hours 20 minutes to reach City 2 and City 1 respectively. If X is moving at 45 kmph, the speed of Y is?
Solution:
By Applying Trick 42,
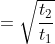
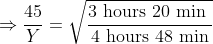

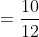
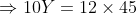
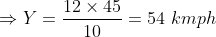
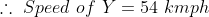
Example-2:
Two trains started at the same time, one from A to B and the other from B to A. If they arrived at B and A respectively 4 hours and 9 hours after they passed each other, the ratio of the speed of the two trains was?
Solution:
By Applying Trick 42,
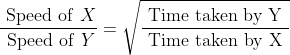
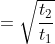

Example-3:
The distance between 2 places R and S is 42 km. Mike starts from R with a uniform speed of 4 kmph towards S and at the same time Jenny starts from S towards R also with some uniform speed. They meet each other after 6 hours. The speed of Jenny is?
Solution:
By Applying Trick 42,
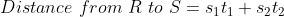
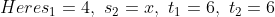


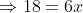
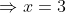
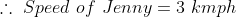
44 Time and Distance - Trick #43
N/A
If both objects run in opposite direction then,
Relative speed = Sum of speeds.
If both objects run in the same direction then,
Relative speed = Difference of Speeds.
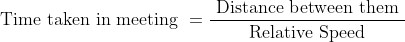
Example-1:
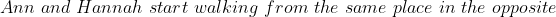
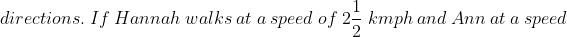

Solution:
By Applying Trick 43,
kmph=\frac{9}{2}\&space;kmph)
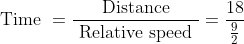
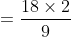

Example-2:
Motor-cyclist M started his journey at a speed of 30 kmph. After 30 minutes, motor-cyclist N started from the same place but with a speed of 40 kmph. How much time (in hours) will N take to overtake M?
Solution:
By Applying Trick 43,
Distance covered by motor cyclist M in 30 minutes
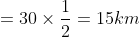
Relative speed = 40 – 30 = 10 kmph
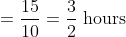
Example-3:
A thief is noticed by a policeman from a distance of 200m. The thief starts running and the policeman chases him. The thief and the policeman run at the rate of 10 kmph and 11 kmph respectively. What is the distance between them after 6 minutes?
Solution:
By Applying Trick 43,
Relative speed of police = 11 – 10 = 1 kmph
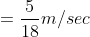
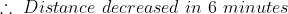
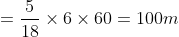
 Distance remained between them = 200–100 = 100 m
Distance remained between them = 200–100 = 100 m
45 Time and Distance - Trick #44
N/A
Let a man take ‘t’ hours to travel ‘x’ km. If he travels some distance on foot with the speed u km/h and remaining distance by cycle with the speed v km/h, then time taken to travel on foot.
}{(v-u)})
Distance travelled on foot = Time × u
Example-1:
A man travelled a distance of 80 km in 7 hrs partly on foot at the rate of 8 km per hour and partly on bicycle at 16km per hour. The distance travelled on the foot is
Solution:
By Applying Trick 44,
Here, x = 80, t = 7 u = 8, v = 16
)
)
)
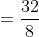
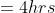
Distance travelled = 4 × 8 = 32 kms
Example-2:
A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot at the rate 4 kmph and partly on bicycle at the rate 9 kmph. The distance travelled on foot is?
Solution:
By Applying Trick 44,
Here, t = 9, x= 61, u = 4, v = 9
)
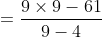

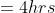
Distance travelled = 4 × 4 = 16 km
46 Time and Distance - Trick #45
N/A
If anyone overtakes or follows another, then
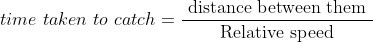
\times\mathrm{\&space;time\&space;}}{\mathrm{\&space;(Difference\&space;of\&space;speeds)\&space;}})
Total travelled distance to catch the thief
\times\mathrm{\&space;time\&space;}}{\mathrm{\&space;(Difference\&space;of\&space;speeds\&space;})})
Example:
A thief is noticed by a policeman from a distance of 500m. The thief starts running and the policeman chases him. The thief and the policeman run at the rate of 10 kmph and 11 kmph respectively. How many minutes will it take to policeman to catch the thief?
Solution:
By Applying Trick 45,
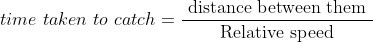
Relative speed = 11 – 10 = 1 kmph
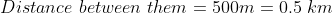
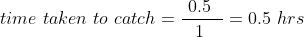
Therefore, time taken to catch the thief = 30 minutes
47 Time and Distance - Trick #46
N/A
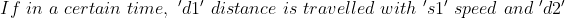
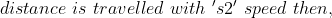
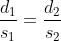
Example:
In a certain time, a man travelled 20 km at a speed of 2kmph. At what speed he needs to travel the distance of 25 km in the same time?
Solution:
By Applying Trick 46,
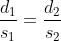
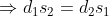
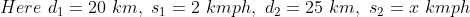
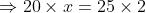
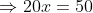

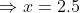
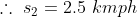
48 Time and Distance - Trick #47
N/A
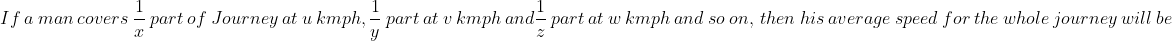

Example:
One third of a certain journey is covered at the rate of 25 kmph, one- fourth at the rate of 30 kmph and the rest at 50 kmph. The average speed for the whole journey is?
Solution:
By Applying Trick 47,
Here, x = 3, u = 25
y = 4, v = 30
z = 12/5, w = 50

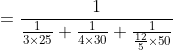
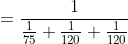
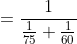
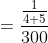
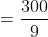
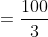
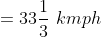
 Time taken in crossing ‘b’ metre length (i.e. platform, bridge, tunnel,standing train etc) by ‘a’ metre length train = total time taken in travelling(a + b) metre by the train.
Time taken in crossing ‘b’ metre length (i.e. platform, bridge, tunnel,standing train etc) by ‘a’ metre length train = total time taken in travelling(a + b) metre by the train.
 Let a train is travelling with the speed x kmph and in the same direction, another train is travelling on parallel path with the speed y kmph, then, Relative speed of the faster train = (x – y) kmph.
Let a train is travelling with the speed x kmph and in the same direction, another train is travelling on parallel path with the speed y kmph, then, Relative speed of the faster train = (x – y) kmph.
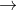 Suppose that a train is travelling with the speed ‘x’ kmph and from the opposite direction another train is coming on parallel path with the speed ‘y’ kmph, then Relative speed of the train = (x + y) kmph.
Suppose that a train is travelling with the speed ‘x’ kmph and from the opposite direction another train is coming on parallel path with the speed ‘y’ kmph, then Relative speed of the train = (x + y) kmph.
50 Trains - Trick #48
N/A
If a train crosses an electric pole, a sitting/ standing man, km or mile stone etc. then,
Distance = Length of train
Length of train = Speed × Time
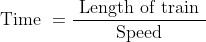
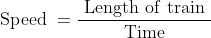
The length of a train and that of a platform are equal. If with a speed of 90 kmph the train crosses the platform in one minute, then the length of the train (in metres) is?
Solution:
By Applying Trick 48,
Let the length of train be x metre Speed = 90 kmph
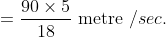
= 25 metre/sec
 Distance covered in 60 sec.
Distance covered in 60 sec.
= 25 × 60 = 1500 metres
Now, according to question,
2x = 1500
 x 750 metre
x 750 metre
51 Trains - Trick #49
N/A
Let ‘a’ metre long train is going with the speed ‘x’ m/s and ‘b’ metre long train is also going with the speed ‘y’ m/s in the same direction on parallel path, then total time taken by the faster train to cross the slower train
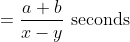
Here, a = 1800, b = 1600
x = = 15 m/s, y = 10 m/s
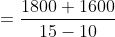
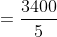
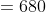
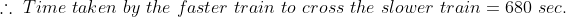
52 Trains - Trick #50
N/A
Let ‘a’ metre long train is going with the speed ‘x’ m/s and ‘b’ metre long train is also going with the speed ‘y’ m/s in the opposite direction on parallel path, then total time taken by the trains to cross each other

Example:
A 1200-metre-long train is going with the speed 22 m/s and 1500 metre long train is also going with the speed 28 m/s in the opposite direction on parallel path, then total time taken by the trains to cross each other?
Solution:
By Applying Trick 50,
Time taken by the trains to cross each other

Here, a = 1200, b = 1500
x = = 22 m/s, y = 28 m/s
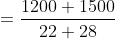
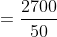
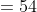
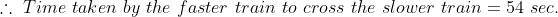
53 Trains - Trick #51
N/A
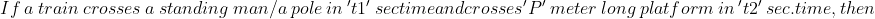
})
Example:
If a train crosses a standing pole in 15 sec time and crosses 120 meter long platform in 25 sec. time, then length of the train is?
Solution:
By Applying Trick 51,
})
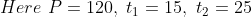
})

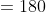
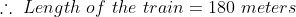
54 Trains - Trick #52
N/A
Let ‘a’ metre long train is running with the speed ‘x’ m/s. A man is running in same direction and with the speed ‘y’ m/s, then
}\&space;seconds)
Example:
A train 180 m long moving at the speed of 20 m/sec. over-takes a man moving at a speed of 10m/ sec in the same direction. The train passes the man in?
Solution:
By Applying Trick 52,
})
Here a = 180, x = 20, y = 10
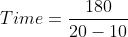
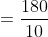
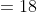
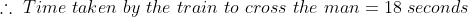
55 Trains - Trick #53
N/A
Let ‘a’ metre long train is running with the speed ‘x’ m/s. A man is running in opposite direction and with the speed ‘y’ m/s, then
}\&space;seconds)
Example:
A train, 240 m long crosses a man walking along the line in opposite direction at the rate of 3 kmph in 10 seconds. The speed of the train is?
Solution:
If the speed of train be x kmph then,
\&space;kmph)
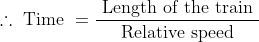
}=\frac{240}{1000(x+3)})
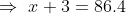

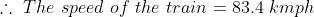
56 Trains - Trick #54
N/A
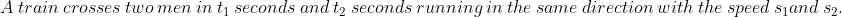

=\left(s_1-s_2\right)\left(\frac{t_1-t_2}{t_1-t_2}\right))
Example:
A train passes two persons walking in the same direction at a speed of 3 kmph and 5 kmph respectively in 10 seconds and 11 seconds respectively.
The speed of the train is?
Solution:
By Applying Trick 54,
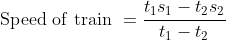
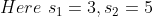
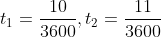

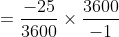

57 Trains - Trick #55
N/A
If two trains of (same lengths) are coming from same direction and cross a man in  seconds, then
seconds, then
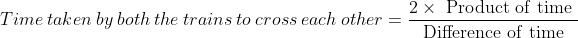
Example:
If two trains A and B of same lengths are coming from same direction and cross a standing pole in 10 and 15 seconds, then time taken by both the trains to cross each other?
Solution:
By Applying Trick 55,
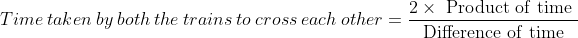
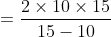
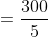
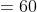
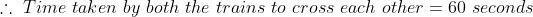
58 Trains - Trick #56
N/A
If two trains of (same lengths) are coming from opposite directions and cross a man in  seconds, then
seconds, then
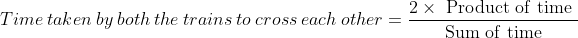
Example:
If two trains A and B of same lengths are coming from opposite directions and cross a standing pole in 20 and 30 seconds, then time taken by both the trains to cross each other?
Solution:
By Applying Trick 56,
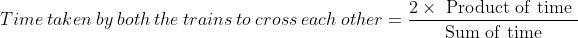
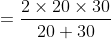
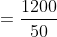
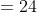
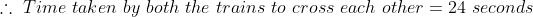
59 Trains - Trick #57
N/A
If a train of length x meters crosses a platform/ tunnel/bridge of length y meters with the speed u m/s in t seconds, then,
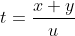
Example:
A train 300 metres long is running at a speed of 25 metres per second. It will cross a bridge of 200 metres in?
Solution:
By Applying Trick 57,
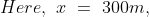

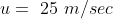
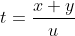
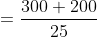
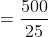
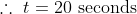
60 Trains - Trick #58
N/A
Two trains A and B, run from stations X to Y and from Y to X with the speed 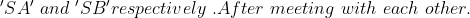
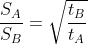
Example:
Two trains started at the same time, one from A to B and the other from B to A. If they arrived at B and A respectively 4 hours and 9 hours after they passed each other, the ratio of the speed of the two trains was?
Solution:
By Applying Trick 58,
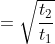

61 Trains - Trick #59
N/A
If a train of length l meters passes a bridge/ platform of 'x' meters in 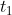 sec, then the time taken by the same train to cross another bridge/platform of length ‘y’ meters is,
sec, then the time taken by the same train to cross another bridge/platform of length ‘y’ meters is,
t_1)
Example:
If a train of length 800 meters passes a bridge of 200 meters in 8 sec, then the time taken by the same train to cross another bridge of length 250 meters is?
Solution:
By Applying Trick 59,
t_1)

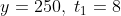
\times8)
\times8)

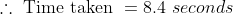
62 Trains - Trick #60
N/A
From stations A and B, two trains start travelling towards each other at speeds a and b, respectively. When they meet each other, it was found that one train covers distance d more than that of another train. The distance between stations A and B is given as
\times&space;d)
Example:
Two trains start from station A and B and travel towards each other at speed of 16 miles/ hour and 21 miles/ hour respectively. At the time of their meeting, the second train has travelled 60 miles more than the first.
The distance between A and B (in miles) is?
Solution:
By Applying Trick 60,
Here, a = 21, b = 16, d = 60
Distance between A and B
\times&space;d)
\times60)

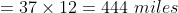
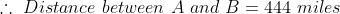
63 Trains - Trick #61
N/A
The distance between two places A and B is x km. A train starts from A towards B at a speed of ‘a’ km/ hr and after a gap of ‘t’ hours another train with speed ‘b’ km/hr starts from B towards A, then both the trains will meet at a certain point after time T. Then, we have.
)
t is taken as positive if second train starts after first train and t is taken as
negative if second train starts before the first train.
Example:
A train starts from City 1 towards City 2 at a speed of 40 kmph and after a
gap of 2 hours another train with speed 50 kmph starts from City 2
towards City 1, then after how many hours both the trains will meet if
the distance between two cities is 170 km?
Solution:
By Applying Trick 61,
)
Here second train starts after first train.
Here, x = 170, a = 40, b = 50, t = 2
}{40+50}\right))
)
= 3 hours.
64 Trains - Trick #62
N/A
A train covers a distance between stations A and B in time 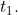 If the speed is changed by S. then the time taken to cover the same distance is
If the speed is changed by S. then the time taken to cover the same distance is  Then the distance (D) between A and B is given by
Then the distance (D) between A and B is given by
\mathrm{\&space;or\&space;}\left(\frac{S^\prime}{t^\prime}\right)t_1t_2)
Where t' : change in the time taken
Example:
A train covers a certain distance between stations P and Q in 4 hours. If the
speed is changed by 10 kmph, then the time taken to cover the same
distance is 3 hours. Then find the distance between P and Q?
Solution:
By Applying Trick 62,
)
Here, S = 10 kmph, 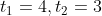
)
)
= 120
Therefore, distance between P and Q is 120 kms.
65 Ratio and Proportion - Formula
N/A
Ratio:
The comparative relation between two amounts/ quantities of same type is called ratio. The ratio of two amounts is equal to a fraction. It shows how much less or more time an amount is in comparison to another.
Ratio always occurs between same units, as –Dollars: Dollars, kg: kg, Hour: Hour, Second: Second etc.
Proportion:
When two ratios are equal to each other, then they are called proportional as 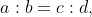 then, a, b, c and d are in proportion
then, a, b, c and d are in proportion
66 Ratio and Proportion - Trick #63
N/A
It does not change the ratio, when we multiply or divide antecedent and consequent of the ratio by a same non–zero number as
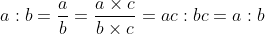
Where c is the non–zero number.
Example:
The ratio of two quantities is 2 to 3. If each of the two quantities is
tripled, what is the ratio of these two new quantities?
Solution:
By Applying Trick 63,
Tripling both quantities in a ratio (or multiplying each by any term, as a
matter of fact) doesn' t change the ratio. If you triple both terms
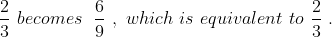
67 Ratio and Proportion - Trick #64
N/A
Mixed ratio:
Let x: y and P: Q be two ratios, then Px : Qy is called mixed ratio.
Example:
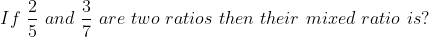
Solution:
By Applying Trick 64,
=\frac{6}{35})
68 Ratio and Proportion - Trick #65
N/A
Duplicate Ratio:
The mixed ratio of two equal ratios is called the duplicate Ratio as
duplicate ratio of a:b is 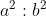
69 Ratio and Proportion - Trick #66
N/A
Sub-duplicate Ratio:
The square root of a certain ratio is called its sub-duplicate.
The sub-duplicate ratio of 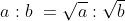
70 Ratio and Proportion - Trick #67
N/A
Triplicate Ratio:
The cube of a certain ratio is called triplicate ratio.
The triplicate ratio of 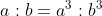
71 Ratio and Proportion - Trick #68
N/A
Sub-triplicate Ratio:
The cube root of a certain ratio is called sub-triplicate ratio as
The Sub-triplicate Ratio of ![a:b=\sqrt[3]{a}:\sqrt[3]{b}](https://latex.codecogs.com/gif.latex?a:b=\sqrt[3]{a}:\sqrt[3]{b})
72 Ratio and Proportion - Trick #69
N/A
Inverse Ratio:
The Reciprocal of quantities of ratio is called its inverse. Reciprocal or inverse ratio of a:b
\times\mathrm{\&space;(L.C.M.\&space;of\&space;}&space;a\mathrm{\&space;and\&space;}&space;b\right))
73 Ratio and Proportion - Trick #70
N/A
Invertendo:
The proportion in which antecedent and consequent quantities change their places, is called invertendo, as
Invertendo of 
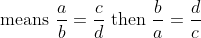
74 Ratio and Proportion - Trick #71
N/A
Alternendo:
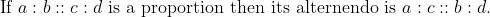
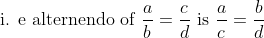
75 Ratio and Proportion - Trick #72
N/A
Componendo:
:&space;b::(c+d):&space;d)
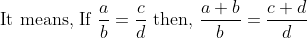
![\text { or, }\left[\frac{a}{b}+1=\frac{c}{d}+1 \Rightarrow \frac{a+b}{b}=\frac{c+d}{d}\right]](https://latex.codecogs.com/gif.latex?\text&space;{&space;or,&space;}\left[\frac{a}{b}+1=\frac{c}{d}+1&space;\Rightarrow&space;\frac{a+b}{b}=\frac{c+d}{d}\right])
76 Ratio and Proportion - Trick #73
N/A
:&space;b::(c-d):&space;d)
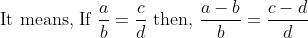
![\text { or, }\left[\frac{ a }{ b }-1=\frac{ c }{ d }-1 \Rightarrow \frac{ a - b }{ b }=\frac{ c - d }{ d }\right]](https://latex.codecogs.com/gif.latex?\text&space;{&space;or,&space;}\left[\frac{&space;a&space;}{&space;b&space;}-1=\frac{&space;c&space;}{&space;d&space;}-1&space;\Rightarrow&space;\frac{&space;a&space;-&space;b&space;}{&space;b&space;}=\frac{&space;c&space;-&space;d&space;}{&space;d&space;}\right])
77 Ratio and Proportion - Trick #74
N/A
Componendo and dividendo:
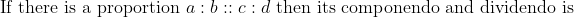
:(a-b)::(c+d):(c-d)&space;\text&space;{&space;or&space;}&space;\frac{a+b}{a-b}=\frac{c+d}{c-d})
To simplify the proportion any one method of componendo, dividendo, componendo and Dividendo can directly be used.
Example:
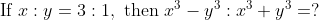
Solution:
By Applying Trick 74,

![\Rightarrow \frac{x^{3}-y^{3}}{x^{3}+y^{3}}=\frac{27-1}{27+1}\text { [By componendo and dividendo] }](https://latex.codecogs.com/gif.latex?\Rightarrow&space;\frac{x^{3}-y^{3}}{x^{3}+y^{3}}=\frac{27-1}{27+1}\text&space;{&space;[By&space;componendo&space;and&space;dividendo]&space;})
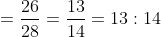
78 Ratio and Proportion - Trick #75
N/A
Mean Proportion:
Let x be the mean proportion between a and b, then 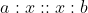 (Real condition)
(Real condition)
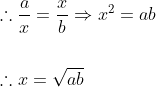
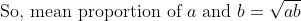
Example:
The mean proportional between &space;\text&space;{&space;and&space;}(12-\sqrt{32})&space;\text&space;{&space;is?&space;})
Solution:
By Applying Trick 75,
(12-\sqrt{32})}&space;\\&space;\\&space;&=\sqrt{(3+\sqrt{2})&space;4(3-\sqrt{2})}&space;\\&space;\\&space;&=2&space;\sqrt{9-2}&space;\\&space;\\&space;&=2&space;\sqrt{7}&space;\end{aligned})
79 Ratio and Proportion - Trick #76
N/A
Third proportional:
Let ‘x’ be the third proportional of a and b then,
)
)
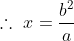
Example:
The third proportional of 12 and 18 is?
Solution:
By Applying Trick 76,

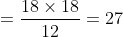
80 Ratio and Proportion - Trick #77
N/A
Fourth proportional:
Let ‘x’ be the fourth proportional of a, b and c then, )
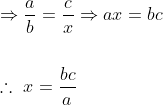
Example:
The fourth proportional to 0.12, 0.21, 8 is?
Solution:
By Applying Trick 77,
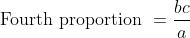
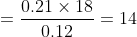
81 Ratio and Proportion - Trick #78
N/A
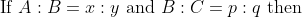
&space;}&space;A:&space;C=x&space;p:&space;y&space;q)
&space;}&space;A:&space;B:&space;C=(x:&space;y)&space;\times&space;p:&space;q&space;y=x&space;p:&space;y&space;p:&space;q&space;y)
It is done as follows:
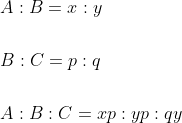
Example-1:
If a, b, c are three numbers such that a : b = 3 : 4 and b : c = 8 : 9, then a : c is equal to?
Solution:
By Applying Trick 78,
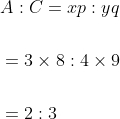
Example-2:
If A : B = 3 : 4 and B : C = 8 : 9, then A : B : C is?
Solution:
By Applying Trick 78,